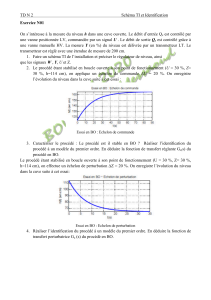
Modélisation /Identification

Modélisation /Identification
L’automatique consiste en l’étude des systèmes réels des
différentes disciplines scientifiques (Electronique,
mécanique, thermique, chimie, écologie, biologie,
économie, sociologie, physique, cosmologie…), en vue de
l’analyse, de la prédiction, de la surveillance, de la
commande, et / ou de l’optimisation des systèmes.
Généralement, la connaissance du modèle du système réel
(on réalise une modélisation) est nécessaire dans l’étude.

Modélisation /Indentification
Identifier un processus (système), c’est chercher un modèle
(dynamique) mathématique, appartenant à une classe de modèles
connue, et qui, soumis à des signaux tests (en entrée), donne une
réponse (dynamique et statique en sortie), la plus proche possible du
système réel .
Pour élaborer un modèle, deux approches sont souvent considérées :
- Modélisation boîte blanche, Elle se fonde sur les lois physiques,
chimiques, mécaniques, biochimiques.
-Modélisation boite noire.La modélisation s’attache à établir « à partir
de données expérimentales, une relation entre les variables des entrées
du processus et les variables de ses sorties et ne nécessite pas a priori la
connaissance des lois physiques.

Modélisation/Identification
Les modèles dynamiques sont de deux sortes :
Modèles non paramétriques
(réponse fréquentielle, réponse à un échelon)
Modèles paramétriques
(fonction de transfert, équations différentielles)
Il existe deux principales classes de méthodes paramétriques :
· - Les méthodes paramétriques graphiques ou déterministes
· - Les méthodes paramétriques statistiques (études stochastiques)

Méthodes paramétriques
graphiques (déterministes)
Méthode de Strejc
Domaine d’application :
Systèmes linéaires à réponse indicielle apériodique
Objectifs :
Approximer la réponse indicielle d’un système donné
par la réponse indicielle d’un système de constante de
temps multiple et comportant éventuellement un retard pur
n
s
)Ts1( ke
)s(U )s(Y
)s(G 

Méthode de Strejc
Système
u(t) y(t)
u(t) u(t)
y(t)
Calcul des paramètres :
Gain statique : k=
)0(u)(u )0(y)(y
Retard : 
Constante de temps T
Ordre du système n
n
20.104 0.736 2.718 0.282 1 2
30.218 0.677 3.695 0.805 2 2.5
40.319 0.647 4.463 1.425 3 2.888
50.410 0.629 5.119 2.100 4 3.219
a
u
T
T
a
m
T
T
T
Ta
T
Tu
T
Ti
T
Tm