L3 Physique et Applications Partiel de Physique des Composants

1
UNIVERSITE PARIS-SUD
CENTRE D'ORSAY
ANNEE 2014-2015
4 mars 2015
L3 Physique et Applications
Partiel de Physique des Composants
Durée 3 heures
Documents non autorisés. Calculatrices autorisées. Les téléphones portables doivent être éteints.
RAPPELS : pour une structure à une dimension suivant x
Equation de Poisson dans un semiconducteur :
2
2
()d d x
dx dx
E
Modèle de dérive-diffusion du courant :
( , )
( , ) . ( , ). . .
n n n n x t
J x t en x t e D x E
( , )
( , ) . ( , ). . .
p p p p x t
J x t e p x t e D x E
Relation d’Einstein :
B
kT
Dµ
e
Equations de continuité :
( , )
( , ) 1 nnn
J x t
n x t GR
t e x
( , )
( , ) 1 ppp
J x t
p x t GR
t e x
Densité d'électrons dans la bande de conduction d'un semiconducteur non dégénéré :
exp FC
CB
EE
nN kT
Densité de trous dans la bande de valence d'un semiconducteur non dégénéré:
exp VF
VB
EE
pN kT
Constantes universelles et données à T = 300 K pour le silicium
kBT = 26 meV NV = 1019 cm-3 NC = 2,8×1019 cm-3 ni = 7,5x109 cm-3 Eg=1,12 eV
µn = 1345 cm2/Vs µp=458 cm2/Vs e = 1,6×10-19 C kB = 1,38×10-23 J.K-1 =8,62×10-5 eV.K-1
0°C=273,15 K h=6,626×10-34 Js=4,136×10-15 eV.s
I. Choix multiples :
Plus d’une réponse peut être correcte. Les mauvaises réponses seront pénalisées.

2
Sur votre copie, notez la (ou les) lettre(s) de la (ou des) réponse(s) correcte(s). Par ex. : 1. a ; 2.
b,c ; 3. d, e,f ; etc.
1. Vous êtes agent secret. Afin de tuer un espion à l’autre bout de la salle dans laquelle vous
êtes emprisonnés tous les deux (vous êtes chacun attaché à un mur), vous ouvrez une
bouteille de poison (contre lequel vous êtes immunisé). Quel(s) phénomène(s) physique(s)
vous permettra/ont de tuer votre adversaire ?
a. La dérive.
b. La diffusion.
c. Le transport balistique.
d. Le dopage.
e. L’équilibre thermique.
f. La faible injection.
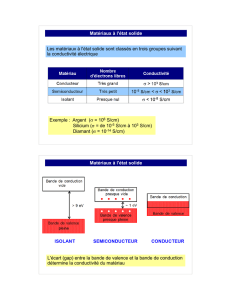
2. On utilise un matériau semiconducteur plutôt qu’un matériau métallique ou isolant afin de
fabriquer un laser ou un détecteur optique parce que:
a. un semiconducteur absorbe de la lumière, quelle que soit l’énergie de celle-ci.
b. un métal absorbe de la lumière, quelle que soit l’énergie de celle-ci.
c. un isolant absorbe de la lumière, quelle que soit l’énergie de celle-ci.
d. La bande de conduction d’un semiconducteur est « vide » (c’est-à-dire, sans états
occupés), à toute température.
e. La bande de conduction d’un métal est « vide » (c’est-à-dire, sans états occupés), à
toute température.
f. La bande de conduction d’un isolant est « vide » (c’est-à-dire, sans états occupés), à
toute température.
g. Un semiconducteur a une bande interdite d’une énergie de l’ordre de celle d’un
photon dans le visible.
h. Un métal a une bande interdite d’une énergie de l’ordre de celle d’un photon dans le
visible.
i. Un isolant a une bande interdite d’une énergie de l’ordre de celle d’un photon dans le
visible.
3. Une semiconducteur « dopé » (par ex. le silicium):
a. Est dit « extrinsèque ».
b. Se comporte à haute température (T>1000°C) comme un semiconducteur très pur.
c. A des impuretés ajoutées qui se placent entre les atomes de silicium dans la maille.
d. A des impuretés ajoutées qui remplacent les atomes de silicium dans la maille.
e. A des impuretés ajoutées qui restent sur la surface.
f. A toujours plus d’électrons dans la bande de conduction qu’un semiconducteur « non-
dopé ».

3
g. A toujours plus de trous dans la bande de valence qu’un semiconducteur « non-
dopé ».
h. A plus de « pep’s » qu’un semiconducteur « non-dopé ».
i. Est un semiconducteur ayant absorbé des substances illicites.
4. Dans les conditions de « faible injection » pour un semiconducteur « dopé » :
a. La concentration des porteurs majoritaires augmente faiblement par rapport à sa
concentration à l’origine (mais cette augmentation ne peut pas être négligée).
b. La concentration des porteurs majoritaires reste à peu près pareille par rapport à sa
concentration à l’origine (cette variation peut être négligée).
c. La concentration des porteurs majoritaires augmente d’une façon significative.
d. La concentration des porteurs minoritaires augmente faiblement par rapport à sa
concentration à l’origine (mais cette augmentation ne peut pas être négligée).
e. La concentration des porteurs minoritaires reste à peu près pareille par rapport à sa
concentration à l’origine (cette variation peut être négligée).
f. La concentration des porteurs minoritaires augmente d’une façon significative.
g. Les porteurs minoritaires sont toujours des trous.
h. La concentration des substances illégales injectées n’est pas très élevée.
5. (Question à lire attentivement) Un semiconducteur non-dégénéré :
a. Possède (au moins) deux niveaux d’énergie à la même énergie précise.
b. A son niveau de Fermi entre EV+3kBT et EC-3kBT
c. Peut utiliser les statistiques de Boltzmann.
d. A n>NC.
e. Peut avoir p>NV.
f. N’est pas « trop » dopé.
g. A gardé ses qualités et sa vigueur d’origine.
II. Dopage et concentration de porteurs en fonction de la température
Vous pourrez considérer que l’ionisation des éléments introduits est complète à T=300K.
1. On dope le silicium avec des atomes accepteurs (NA=1014 cm-3). Quel type de charges libres
a-t-on libéré ?
2. Quelles sont les valeurs des concentrations en électrons et en trous (T=300K)?
3. Variation de la concentration des porteurs en fonction de la température : pour le cas
des atomes accepteurs,
a. tracer soit la concentration des porteurs majoritaires en fonction de la température,
soit le logarithme de la concentration des porteurs majoritaires en fonction de 1/T.

4
b. Identifier les trois régimes différents.
c. Tracer des diagrammes de bandes pour les trois régimes différents afin d’expliquer ce
qui se passe dans ces trois différentes gammes de températures. Sur votre schéma,
inclure quelques niveaux d’énergie des dopants et dessiner quelques porteurs.
d. Donner une expression pour la concentration des porteurs majoritaires dans le régime
de température moyenne.
e. Trouver une expression pour la concentration des porteurs majoritaires dans le
régime de haute température (en fonction de Nc, Nv, Eg, kB, T).
4. A partir du 8 mars 2015, les détecteurs de fumée sont obligatoires dans les logements en
France. Pour encore plus de sécurité, vous décidez de vous fabriquer un détecteur de
chaleur. Vous fabriquez un dispositif où une alarme sonnera lorsque la concentration des
porteurs majoritaires changera rapidement en fonction de 1/T où T, la température, est égale
à 40°C.
a. Trouver une expression pour Tmax, la température à laquelle on passe du régime de
haute température au régime de température moyenne cités en III.3.d. et e.
b. Evaluer Tmax pour le cas du Si avec le dopage ci-dessus (III.1). Pourriez-vous utiliser
ce morceau de silicium pour votre détecteur de chaleur ? Justifier votre réponse.
c. Si vous avez répondu négativement, à III.4.b, quel matériau et quel dopage
utiliseriez-vous ? (voir tableau ci-dessous)
GaAs
Ge
Eg(eV); énergie de gap
1,42
0,66
Nc (cm–3); densité effective
d’états dans la bande de
conduction
4,7x1017
1 x1019
Nv (cm–3); densité effective
d’états dans la bande de
valence
7x1018
6x1018
III. Photoconduction
On éclaire une tranche de silicium dopé n de résistivité 0 = 2 .cm et d'épaisseur ep = 250 µm
par une lumière monochromatique  = 1 µm sous un flux de 10 W.cm-2.
a. Calculer le flux de photons incidents (cm-2s-1) et le nombre de photons absorbés par unité de
surface par unité de temps dans l'épaisseur de la tranche (=0e-x avec  = 1 cm-1 et  en
cm-2s-1).
b. Sachant que chaque photon absorbé crée une paire électron-trou, calculer la vitesse de
création (taux de génération) G supposée uniforme dans toute l'épaisseur de la tranche.
Justifier l’hypothèse d’uniformité.
c. La durée de vie étant de  = 10 µs et les mobilités des électrons et des trous étant
respectivement µn = 1500 cm2.V-1.s-1 et µp = 400 cm2.V-1.s-1, quelle est la résistivité de la
tranche éclairée ?

5
IV. Interprétation des diagrammes de bandes (énergie d’un électron en
fonction de la position)
Un dispositif en silicium à 300 K est caractérisé par le diagramme de bande ci-dessous. Ec est
l’énergie du bas de la bande de conduction, Ev est l’énergie du haut de la bande de valence, EF
est l’énergie de Fermi et Ei est l’énergie de Fermi intrinsèque. L est la longueur du dispositif dans
la direction x. Utiliser le diagramme de bande ci-dessous afin de répondre aux questions
suivantes.
1. Le dispositif est-il à l’équilibre thermodynamique ? Expliquer.
2. Le semiconducteur est-il partout « dégénéré » ou partout « non-dégénéré » ? Si tel
est le cas, expliquez pourquoi. Sinon, expliquez pourquoi et donnez les régions
(approximatives) où le semiconducteur est soit « dégénéré » soit « non-dégénéré ».
3. Quel est le type de dopant (dominant)
a) à x=0 ?
b) à x=L/2 ?
c) à x=L ?
d) Expliquer vos réponses a) à c).
3. Quelles sont les concentrations d’électrons dans la bande de conduction et de trous
dans la bande de valence à x=L/2 ?
4. Quelles sont les concentrations d’électrons dans la bande de conduction et de trous
dans la bande de valence à x=3L/5?
5. Prenons comme hypothèse que EC a la forme (EC - EF) =-a(x-b)2+c pour x entre L/2 et
L. BONUS : Trouver a, b et c. (A x=L, la pente est nulle).
6. Tracer la variation du potentiel en fonction de x
7. Trouver une expression pour le potentiel (en fonction de a, b, et c si vous voulez).
8. Trouver une expression pour le champ électrique.
9. Trouver la valeur du champ électrique pour L=0,8 cm à
a) x=L/4
b) x=L
c) x=3L/5
10. Quelle est la valeur du courant total dans le dispositif ? Expliquer votre réponse.
11. Le courant de diffusion est-il nul à x=3L/5 ? Expliquer votre réponse. S’il est non-nul,
donner sa valeur pour L=0,8 cm (avec a=1 eV/µm2, b=2 µm et c=3 eV, si vous n’avez pas
répondu à IV.5).
12. En général, quelle condition permet d’avoir un courant de diffusion dans un
semiconducteur ?