N - Etud.insa

DGEI-INSA-Toulouse ...................................................................... Patrick TOUNSI
1
Concentration de porteurs en surface dans une
structure Métal-Isolant-Semiconducteur
Introduction:
Les transistors MOS sont utilisés dans un très grand nombre de montages, qu’ils soient
linéaires ou numériques. De nombreuses structures intégrées ont été développées sur le même
principe que celui du transistor MOS. Il est donc important d’étudier le principe de fonctionnement
de ce type de structures.
Comme vous l’avez vu en cours, l’étude du transistor MOS fait beaucoup appel aux notions
de l’électrostatique. En effet, avant même de faire passer un courant entre le drain et la source du
MOS, il faut d’abord s’assurer de l’existence de porteurs en nombre suffisant dans le canal (sous
l’oxyde de grille). Le principe même du fonctionnement du transistor MOS est basé sur la
concentration de ces porteurs dans le canal (ce qui module sa résistivité). Ce papier a pour objet de
vous donner les principes du calcul de la concentration de porteurs qui serviront à la conduction
entre drain et source.
Hypothèses
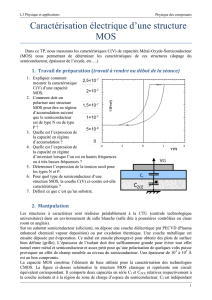
Soit la structure MIS représentée par la figure suivante:
Va
x
x = 0
Métal
Isolant
Semiconducteur
OU

DGEI-INSA-Toulouse ...................................................................... Patrick TOUNSI
2
On considère que le semiconducteur est à dopage uniforme.
Le problème est considéré unidimensionnel, les grandeurs physiques ne varient que suivant
l’abscisse x, et restent constantes suivant les autres axes (y et z).
Considérons le cas général d’un semiconducteur dopé N= ND-NA, qui pourrait être de type N
si ND>>NA ou de type P si NA>>ND.
Calcul du champ électrique et du potentiel électrostatique
Dans ce semiconducteur l’équation de Poisson s’écrit:
d2V
dx2=−
ρ
ε
=−qp
−
n
+
N
(
)
ε
(1)
ε: permittivité [F/cm]
p
et n : respectivement les concentrations de trous et d’électrons à l’équilibre
thermodynamique.
ρ: concentration de porteurs [cm-3]
V: potentiel électrostatique qui est par ailleurs lié aux concentrations de porteurs n et p par les
relations suivantes:
V=UTln n
ni
⎛
⎝
⎜ ⎞
⎠
⎟ =−UTln p
ni
⎛
⎝
⎜
⎞
⎠
⎟ (2)
ni: concentration intrinsèque ni2=n
p
Multiplions les deux membres de (1) par 2dV
dx , on alors:
2
dV
dx d2V
dx2=−2q
ε
p−n+N
()
dV
dx (3)
La relation (3) peut aussi s’écrire:
d
dx dV dx
⎛
⎝ ⎞ ⎠
2
=−2q
ε
p−n+N
()
dV
dx (4)

DGEI-INSA-Toulouse ...................................................................... Patrick TOUNSI
3
Par ailleurs, si nous cherchons le gradient du potentiel électrostatique, c’est à dire dV
dx à partir
de la relation (2) on a:
dV
dx =UT
ndn dx =−UT pdp dx (5)
On remplace dV
dx dans (4) par son expression (5), on obtient:
d
dx dV dx
⎛
⎝ ⎞ ⎠
2
=2q
ε
UTdp
dx +dn dx −N
ndn
dx
⎛
⎝
⎜ ⎞
⎠ (6.a)
Ou;
d
dx dV dx
⎛
⎝ ⎞ ⎠
2
=2q
ε
UTdp
dx +dn dx +N
pdp
dx
⎛
⎝
⎜ ⎞
⎠ (6.b)
En remarquant que d
V
dx représente au signe près le champ électrique E, la relation (6.a) peut
alors s’écrire: (cas unidimensionnel)
dE
2
()
=2q
ε
UTdp+dn−Ndn
n
⎛
⎝
⎜ ⎞
⎠ (7.a)
Sachant que le champ électrique au loin dans le volume du semiconducteur (loin du métal) est
nul, nous pouvons déterminer sa valeur à l’interface isolant-semiconducteur, c’est à dire x=0, en
intégrant (7.a).
Il est évident que l’abscisse x=0 ne signifie rien si l’on ne précise pas les grandeurs physiques
qui caractérisent cette position. A l’interface isolant-semiconducteur la concentration des porteurs
est n
s et
p
s (en surface), celle-ci au loin devient n v et
p
v.
L’intégration de (7.a) entre x=0 (en surface) et x->∞ (en volume) s’écrira:
(en sachant que N est constant suivant x car le dopage est uniforme)
Es
2−Ev 2=2q
ε
UTdp
pv
ps
∫+dn
nv
ns
∫−Ndn
n
nv
ns
∫
⎡
⎣
⎢
⎤
⎦
⎥
(8.a)
Comme Ev est pratiquement nul, on alors:
Es
2=2q
ε
UTps−pv
()
+ns−nv
()
−Nln ns
nv
⎡
⎣
⎢ ⎤
⎦
⎥
(9.a)

DGEI-INSA-Toulouse ...................................................................... Patrick TOUNSI
4
Sachant par ailleurs que le champ électrique en surface de l’interface Es est lié à la charge
surfacique Qs [cm-2] par la relation:
Qs
=
−
ε
E
s (10)
En remplaçant Es2 dans (9.a) par la relation (10) on obtient:
Qs
2=2q
ε UTps−pv
()
+ns−nv
()
−Nln ns
nv
⎡
⎣
⎢ ⎤
⎦
⎥
(11.a)
Voici donc l’expression générale de la concentration surfacique des porteurs susceptibles
d’assurer la conduction dans le canal d’un transistor MOS.
Remarque 1: Vérifier la compatibilité des unités (équation aux dimensions) dans cette
dernière expression.
Remarque 2: Pour faire ce calcul, nous sommes partis de l’expression (6.a). Vous pouvez tout
aussi bien partir de (6.b). On aboutit alors à l’expression:
Qs
2=2q
ε UTps−pv
()
+ns−nv
()
+Nln ps
pv
⎡
⎣
⎢
⎤
⎦
⎥
(11.b)
Comme il est dit plus haut, l’expression de la charge surfacique à l’interface isolant-
semiconducteur donnée par (11.a) ou (11.b) est générale. Nous allons donc examiner son
expression dans des cas bien précis.
Accumulation
Considérons que nous avons affaire à un semiconducteur de type N, avec une concentration
de dopant ND.
L’accumulation en surface signifie que la concentration des électrons au niveau de l’interface
isolant-semiconducteur ns est très supérieure à celle existant en volume n
v≅ND.
Donc n
s>> ND≅n v.
D’autre part, comme notre semiconducteur est supposé de type N affirmé, donc
p
v≅ni2/ND est
négligeable, et il est d’autant plus négligeable à l’interface
p
s<<ni2/ND, puisque p sn s=ni
2
Donc n
v ,
p
v , et
p
s sont tous négligeables devant n s.
De plus: ln ns
nv<< ns ND
avec nv≅ND

DGEI-INSA-Toulouse ...................................................................... Patrick TOUNSI
5
d’où:
NDln ns
nv<< ns
Finalement, de l’expression de Qs il ne restera que:
Qs
2
≅
2q
ε
UTns (12)
Pour obtenir une approximation de l’étendue Wacc de cette zone d’accumulation on admet
que la concentration n
s des électrons dans toute cette zone reste uniforme.
Wacc ≅Qs
qns
D’où l’extension de la zone d’accumulation:
Wacc ≅2
ε UT/qns (13)
Dépeuplement
Lorsqu’il y a création d’une zone dépeuplée, la concentration de porteurs libres est quasi-
nulle, la zone étant désertée par les porteurs libres majoritaires. Donc en surface, au niveau de
l’interface isolant-semiconducteur on a n
s<< ND≅n v.
D’autre part n
s >>
p
v et n
s>>
p
s (semiconducteur de type N)
Comme n
s<< n v on a alors:
ln
ns
nv>>1
Donc: NDln ns
nv>> ND≅n
v
De l’expression de Qs ne restera que:
Qs
2≅2q
ε UTNDln ND
ns
⎛
⎝
⎜
⎞
⎠
⎟ (14)