On cherche à modéliser de deux façons différentes l

EXERCICE 4 (7 points )
(Commun à tous les candidats)
On cherche à modéliser de deux façons différentes l’évolution du nombre, exprimé en millions, de
foyers français possédant un téléviseur à écran plat en fonction de l’année.
Les parties A et B sont indépendantes
Partie A : un modèle discret
Soit unle nombre, exprimé en millions, de foyers possédant un téléviseur à écran plat l’année n.
On pose n= 0 en 2005, u0= 1 et, pour tout n≥0,un+1 =1
10un(20 −un).
1. Soit fla fonction définie sur [0; 20] par f(x) = 1
10x(20 −x).
a. Etudier les variations de fsur [0; 20].
b. En déduire que pour tout x∈[0; 10],f(x)∈[0; 10].
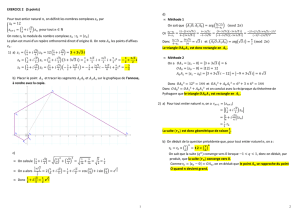
c. On donne ci-dessous la courbe représentative Cde la fonction fdans un repère orthogonal.
Représenter à l’aide de ce graphique les cinq premiers termes de la suite (un)n≥0sur l’axe
des abscisses.
2. Montrer par récurrence que pour tout n∈N,0≤un≤un+1 ≤10.
3. Montrer que la suite (un)n≥0est convergente et déterminer sa limite.
Partie B : un modèle continu
Soit g(x)le nombre, exprimé en millions, de tels foyers l’année x.
On pose x= 0 en 2005,g(0) = 1 et gest une solution qui ne s’annule pas sur [0; +∞[de l’équation
différentielle
(E) : y′=1
20y(10 −y).
1. On considère une fonction yqui ne s’annule pas sur [0; +∞[et on pose z=1
y.
a. Montrer que yest solution de (E)si et seulement si zest solution de l’équation différentielle :
(E1) : z′=−1
2z+1 20.
b. Résoudre l’équation (E1)et en déduire les solutions de l’équation (E).
Page 5 / 6

2. Montrer que gest définie sur [0; +∞[par g(x) = 10
9e−1
2x+ 1.
3. Etudier les variations de gsur [0; +∞[.
4. Calculer la limite de gen +∞et interprétez le résultat.
5. En quelle année le nombre de foyers possédant un tel équipement dépassera-t-il 5millions?
2 4 6 8 10 12 14 16 18 20 22
x
2
4
6
8
10
y
12
Page 6 / 6

EXERCICE 4
Partie A : un modèle discret
1) a. Pour tout réel xde [0;20],f(x) = 1
10 (20x −x2).fest dérivable sur [0;20]et pour tout réel xde [0;20],
f′(x) = 1
10 (20 −2x) = 1 5(10 −x). On en déduit le :
Tableau de variations de f.
x010 20
f′(x) + 0−
10
f
0 0
b. fadmet donc un minimum égal à 0atteint en x=0et x=20 et un maximum égal à 10 atteint en x=10. Donc,
pour tout x∈[0;20],f(x)∈[0;10].
c. Représentation graphique de la suite (un)n∈N.
u0u1u2u3u4
2 4 6 8 10 12 14 16 18 20 22
x
2
4
6
8
10
y
12
y=x
y=f(x)
2) Montrons par récurrence que pour tout entier naturel n,0≤un≤un+1≤10.
•On a u0=1puis u1=f(u0) = 19
10 =1, 9 et donc 0≤u0≤u1≤10.
•Soit n∈N. Si 0≤un≤un+1≤10. Puisque fest croissante sur [0;10], on a f(0)≤f(un)≤f(un+1)≤f(10)ce qui
s’écrit encore 0≤un≤un+1≤10.
On a montré par récurrence que
pour tout entier naturel n,0≤un≤un+1≤10.
http ://www.maths-france.fr 7 c Jean-Louis Rouget, 2008. Tous droits réservés.

3) La suite (un)n∈Nest croissante et majorée par 10. On en déduit que la suite (un)n∈Nconverge vers un réel que l’on
note ℓ. De plus, comme pour tout entier n, on a 1≤un≤10 (car u0=1et car la suite (un)n∈Nest croissante), quand n
tend vers +∞, on obtient 1≤ℓ≤10. Ensuite, pour tout entier naturel n, on a un+1=1
10 un(20 −un)et quand ntend
vers +∞, on obtient ℓ=1
10 ℓ(20 −ℓ)puis 10ℓ =ℓ(20 −ℓ)puis 10 =20 −ℓ(car ℓ6=0) et enfin ℓ=10.
La suite (un)n∈Nconverge et lim
n→∞ un=10.
Partie B : un modèle continu
1) a. Soit yune fonction dérivable sur [0, +∞[ne s’annulant pas sur [0, +∞[. Posons alors z=1
y.
zest définie, dérivable sur [0; +∞[, ne s’annule pas sur [0; +∞[et de plus y=1
zet donc y′= − z′ z2. Mais alors,
y′=1
20 y(10 −y)⇔y′=1 2y−1 20 y2⇔−z′ z2=1 2
1
z−1 20
1
z2⇔z′= − 1 2z+1 20 .
b. Soient aet bdeux réels. On sait que les solutions sur Rde l’équation différentielle y′=ay +bsont les fonctions de la
forme x7→Ceax −b
a. Ici, a= − 1 2et b=1 20 . Donc
les solutions de (E1)sur Rsont les fonctions de la forme x7→Ce−x/2 +1
10 ,C∈R.
Si une telle fonction ne s’annule pas sur [0; +∞[, elle fournit une solution de (E)sur [0; +∞[à savoir la fonction
x7→1
Ce−x/2 +1
10
.
2) D’après ce qui précède, il existe une contante réelle Ctelle que pour tout x≥0,g(x) = 10
10Ce−x/2 +1. L’égalité
g(0) = 1fournit 1
C+1
10
=1puis C+1
10 =1et donc C=9 10 . Donc, pour tout réel x≥0,
g(x) = 1
9
10 e−x/2 +1 10
=10
9e−x/2 +1.
Pour tout réel positif x,g(x) = 10
9e−x/2 +1.
3) La fonction gest dérivable sur [0; +∞[en tant que quotient de fonctions dérivables sur [0; +∞[dont le dénominateur
ne s’annule pas sur [0; +∞[et pour x≥0
g′(x) = 10 ×−(9e−x/2 +1)′
(9e−x/2 +1)2=10 ×
−9×−1
2×e−x/2
(9e−x/2 +1)2=4, 5e−x/2 (9e−x/2 +1)2.
g′est strictement positive sur [0; +∞[et donc
gest strictement croissante sur [0; +∞[.
4) lim
x→+∞e−x/2 =lim
X→−∞
eX=0et donc lim
x→+∞g(x) = 10
0+1=10.
lim
x→+∞g(x) = 10.
http ://www.maths-france.fr 8 c Jean-Louis Rouget, 2008. Tous droits réservés.

5) Soit xun entier naturel.
g(x)≥5⇔10
9e−x/2 +1≥5
⇔9e−x/2 +1
10 ≤1 5(par décroissance de la fonction x7→1 xsur ]0, +∞[et car 9e−x/2 +1 > 0)
⇔9e−x/2 +1≤2⇔9e−x/2 ≤1⇔e−x/2 ≤1
9
⇔ln(e−x/2)≤ln 1
9(par croissance de la fonction ln sur ]0; +∞[)
⇔−x
2≤−ln 9⇔x≥2ln 9
⇔x≥4, 3 . . . ⇔x≥5(car xest entier).
x=5correspond à l’année 2010 et donc
Le nombre de foyers possédant un téléviseur à fond plat dépassera 5millions à partir de l’année 2010.
http ://www.maths-france.fr 9 c Jean-Louis Rouget, 2008. Tous droits réservés.