corrigés

1
PHYS-F-104
Physique
Interrogation du 3 nov. 2010
I. Théorie (10 points – 40 min.)
1. Montrez qu’il existe deux angles de tir pour atteindre une cible située à une distance
donnée d’un canon (la cible et la bouche du canon sont supposées à la même hauteur).
Quelle est la relation entre ces deux angles ?
(3 points)
Dans le plan vertical, le mouvement est uniformément accéléré
=> vz = a t +v0z => le temps de montée est t = v0 sin / g
Le temps total est le double du temps de montée
Le mouvement horizontal est uniforme => x = vx t
=> la portée est xP = 2 (v0 cos (v0 sin / g) = 2 v02/g sincos
Comme sin(2 - cos et cos (2 - sinl’équation admet deux solutions
complémentaires
2. Une pierre de masse m est accrochée au bout d’une corde qui tourne dans le plan
vertical. Exprimez la tension dans la corde en fonction de l’angle que celle-ci forme avec
l’horizontale, et en fonction éventuellement d’autres variables.
(2 points)
Comme le mouvement de la pierre est circulaire, la résultante des forces agissant sur la pierre
doit avoir une composante centripète.
Les composantes centripètes des forces agissant sur la pierre sont la tension T dans la corde et
la composante du poids dirigée selon la corde.
On prend la direction positive vers le centre de rotation.
La composante du poids dirigée vers le centre de rotation est –mg cos, où g est la norme de
l’accélération gravitationnelle et  est l’angle entre la corde et la verticale (angles à côtés
parallèles), soit encore -mg cos(2 - mg sin
=> Fc = m 2 R = T - mg sin
=> T = m (2 R + g sin
3. Exprimez en une formule la loi des frottements cinétiques solide-solide, en expliquant
la signification de chacun des symboles utilisés et en justifiant la formule par les lois
empiriques du frottement.
(2 points)
La loi est Ff = - c |FN| 1v
Le vecteur Ff représente la force de frottement
Le vecteur FN représente la composante normale de la réaction du support ; la force de
frottement est proportionnelle à son module
Le coefficient de frottement c dépend de la nature des surfaces en contact, et de rien d’autre
Le vecteur 1v est le vecteur unitaire dirigé dans la direction et le sens de la vitesse ; le signe –
indique que la force de frottement est opposée au mouvement

2
4. Enoncez les trois lois de Kepler
(3 points)
1. Les planètes décrivent des orbites elliptiques, le Soleil étant situé en l’un des foyers
2. Le rayon vecteur joignant le Soleil à la planète balaie des aires égales en des temps égaux
3. Le rapport du cube de la longueur du demi-grand axe de l’orbite de la planète (dans le cas
d’orbites circulaires, le rayon de l’orbite) au carré de sa période est le même pour toutes les
planètes
II. Exercices (10 points – 50 min.)
1. Une pièce de monnaie de 20 g est posée sur la platine d’un tourne-disque qui effectue
75 tours par minute. Le coefficient de frottement statique est de 0,50.
A quelle distance du centre de la platine la pièce doit-elle être posée pour qu’elle ne se
mette pas à glisser ?
(4 points)
La pièce décrit un mouvement circulaire, pour lequel la force centripète est fournie par le
frottement statique => m  R < S m g
où  = 75 tours / min = 75 x 2 / 60 rad / s => R < 0,081 m
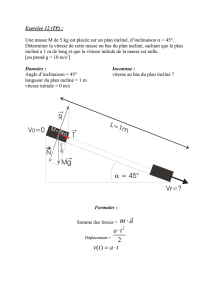
2. Un objet est lancé vers le haut sur un plan incliné parfaitement lisse posé sur le sol,
long de 3,5 m et faisant un angle de 30° avec l’horizontale.
Arrivé au haut du plan incliné, l’objet décrit une trajectoire dans le vide et il retombe
sur le sol après 2,5 s.
Quelle doit être la vitesse de l’objet au pied du plan incliné ?
(Idéalisation du mouvement d’un snow-board, où une figure acrobatique doit être
réalisée en 2,5 s)
(6 points)
Prenons l’axe y dirigé vers le haut, avec y = 0 au niveau du sol.
Le mouvement de l’objet dans l’air est donné selon l’axe vertical par la loi
y = ½ ay t2 + v0y t + y0 où
y = 0 m est la coordonnée à la fin du mouvement
ay = g = - 10 m/s2
y0 = L sin= 1,75 m est la coordonnée du sommet du plan incliné, avec L = 3,5 m la
longueur du plan incliné et  30° son angle avec l’horizontale
On trouve donc pour v0y
v0y = (-½ g t2 - y0) / t = 11,8 m/s
La vitesse que doit avoir l’objet au sommet du plan incliné est v = v0y / sin 
=> v = 23,6 m/s
Sur le plan incliné, l’objet accomplit un mouvement uniformément décéléré, pour lequel
l’accélération est donnée par la composante du poids parallèle au plan incliné
a = g sin - 5 m/s2
On obtient la vitesse v0 au bas du plan incliné à partir de la formule v2 = v02 + 2 a s, valable
pour un mouvement uniformément accéléré, avec ici v = 23,6 m/s, a = -7,21 m/s2 et s = 3,5 m
=> v0 = 24,3 m/s => 24 m/s