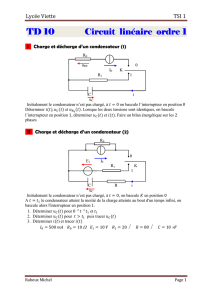
principe fondamental de la dynamique

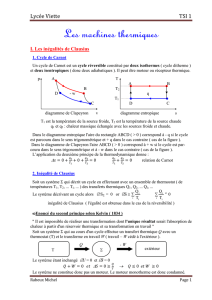
Lycée Viette TSI 1
Rabeux Michel Page 1
Principe fondamental
Principe fondamentalPrincipe fondamental
Principe fondamental
de la dynamique
de la dynamiquede la dynamique
de la dynamique
II . Les quatre interactions fondamentales
1. Les quatre interactions fondamentales
Les interactions entre les systèmes peuvent se présenter sous quatre formes.
 les interactions gravitationnelles : forces s’exerçant à distance entre deux masses
Les interactions entre le Soleil et la Terre, entre un objet et le terre sont des interactions
gravitationnelles. Elles sont à portée infinie
 les interactions électromagnétiques : forces s’exerçant à distance entre deux charges
Les forces de frottement, la tension d’un fil sont des interactions électromagnétiques.
Elles sont à portée infinie
 les interactions fortes : forces d’interactions de courte portée ( qq fm ) entre certaines
particules élémentaires ( par exemple entre protons et neutrons dans un noyau )
Ces interactions sont très intenses.
 les interactions faibles : interactions de courtes portées ( qq   ) et peu intenses
Elles sont responsables de la radioactivité β
2. Notion de forces
Une force caractérise l’action d’un système matériel sur un point matériel . Cette force
peut dépendre à la fois de la nature physique de  et du système, des positions et vitesses de
 et du système. Une force peut modifier un mouvement ou déformer un système.
La mécanique newtonienne postule l'invariance de la force vis à vis de tout changement de
référentiel et l’additivité des forces. L'unité de la force est le newton ( N ).
Il existe deux familles de forces : forces à distances ou forces de contact.
Leurs origines sont soit gravitationnelle, soit électrostatique.
3. Exemples de forces
 Force de gravitation 
et  sont les masses gravitationnelles
 Force de pesanteur ( poids ) ( très peu différente de la force de gravitation ) 
 Force coulombienne 
 Force électromagnétique de Lorentz  ∧
 Réaction du support avec ou sans frottements
Lorsque le point matériel  évolue sur un support solide, ce dernier exerce une force
sur . Cette force s’appelle la réaction du support  . Elle peut être décomposée en
une composante normale  et une composante tangentielle
La réaction normale est la force qui empêche le point  de traverser le support

Lycée Viette TSI 1
Rabeux Michel Page 2
La réaction tangentielle représente la force de frottement exercée par le support sur le
point  Le sens de la réaction tangentielle est toujours opposé au mouvement
potentiel du point  par rapport au support. Lorsque l’on néglige les frottements entre
 et le support, la réaction tangentielle est nulle.
Il existe des relations entre les normes des deux composantes. Ces relations diffèrent
selon que le point  est en mouvement ou immobile par rapport au support : ce sont
les lois de Coulomb.
Si le point  est en mouvement par rapport au support : 
avec 
 le coefficient de frottement ( sans dimension ) qui dépend de
l’état des surfaces en contact.
Si le point  est au repos par rapport au support : 
Remarque : si le point  quitte le support ( liaison unilatérale ) la réaction s’annule.
 Forces de frottement fluide
Lorsqu’un corps solide se déplace dans un fluide ( gaz ou liquide ), il est soumis à une
force de frottements de la part du fluide. Cette force de frottement est à chaque instant
colinéaire et de sens opposé au mouvement du point  
Pour de faibles vitesses du point , la norme de la force est proportionnelle à la norme
de la vitesse du point 
Pour les vitesses plus élevées, en première approximation, la force varie comme le
carré de la vitesse 
 est le maître couple  dépend de la forme de l’objet et du fluide
Remarque : il existe aussi une force perpendiculaire au déplacement appelée la
portance ( qui permet aux avions de voler )

Lycée Viette TSI 1
Rabeux Michel Page 3
 Tension d’un fil : le fil est fixé en une de ses extrémités à un point O et à l’autre
extrémité est accroché le point matériel M. La force exercée par le fil sur le point M
s’appelle la tension du fil.
On supposera le fil « idéal » : c’est-à-dire sans masse, sans raideur et inextensible.
Lorsqu’il est tendu, la force exercée par le fil sur le point matériel est : colinéaire au
fil, dirigée du point M vers le point O, sa norme est a priori inconnue, elle dépend des
autres forces auxquelles est soumis le point matériel.
Lorsqu’il n’est pas tendu, le fil n’exerce aucune force.
Une poulie idéale transmet la tension du fil
 Tension d’un ressort :    est la raideur du ressort  est la longueur du
ressort et  la longueur à vide du ressort. Cette force ( de rappel ) tend à ramener la
longueur du ressort à sa longueur à vide.
 ressort détendu
 ressort allongé
 Forces de pression :  avec  la pression,  la surface élémentaire
sur laquelle s’exerce la force,  la normale à la surface élémentaire dirigée vers
l’extérieur.

Lycée
Viette TSI 1
Rabeux Michel
 L
a poussée d’Archimède ( résultante de forces de pression )
du fluide déplacé par l’objet.
III .
Les trois lois de Newton
1.
La première loi de Newton
Enoncé
Il existe au moins un référentiel
éloigné de tout autre corps (isolé c’est à dire soumis à aucune force de la part
de l’extérieur )
, possède un mouvement rectiligne uniforme (ou un état de
repos).
Un tel référentiel est dit
galiléen
rapport à un référentiel galiléen est aussi galiléen.
Le référentiel
de Copernic
pour origine le centre de masse du système solaire ( assimilable au centre du soleil ), les trois
axes se dirigent vers trois étoiles très éloignées et considérées comme fixes par r
galaxie.
Le
référentiel héliocentrique ou de Kepler
Les trois axes sont identiques aux trois axes du référentiel de Copernic.
Le référentiel géocentrique
aux axes précédemment définis ) est en translation elliptique ( quasi circulaire par rapport à
ℜ
C
).
Il n'est donc pas rigoureusement galiléen, mais il sera considéré comme galiléen pour des
expérien
ces dont la durée est faible devant une année ( période de révolution de la terre autour
du soleil ) et dont les déplacements sont faibles devant la dimension de l'orbite terrestre.
Viette TSI 1
a poussée d’Archimède ( résultante de forces de pression )
: c’est l’opposé du poids
du fluide déplacé par l’objet.
Les trois lois de Newton
La première loi de Newton
: principe de l’inertie
Il existe au moins un référentiel
ℜ
ℜℜ
ℜ
par rapport auquel tout point matériel M,
éloigné de tout autre corps (isolé c’est à dire soumis à aucune force de la part
, possède un mouvement rectiligne uniforme (ou un état de
galiléen
. Tout référentiel en translation rectiligne et uniforme par
rapport à un référentiel galiléen est aussi galiléen.
de Copernic
ℜ
C
réalise un excellent référentiel galiléen. Ce référentiel a
pour origine le centre de masse du système solaire ( assimilable au centre du soleil ), les trois
axes se dirigent vers trois étoiles très éloignées et considérées comme fixes par r
référentiel héliocentrique ou de Kepler
ℜ
K
a pour origine le centre d’inertie du soleil.
Les trois axes sont identiques aux trois axes du référentiel de Copernic.
ℜ
0
( origine
: centre de la terre, les trois axes sont identiques
aux axes précédemment définis ) est en translation elliptique ( quasi circulaire par rapport à
Il n'est donc pas rigoureusement galiléen, mais il sera considéré comme galiléen pour des
ces dont la durée est faible devant une année ( période de révolution de la terre autour
du soleil ) et dont les déplacements sont faibles devant la dimension de l'orbite terrestre.
Viette TSI 1
Page 4
: c’est l’opposé du poids
par rapport auquel tout point matériel M,
éloigné de tout autre corps (isolé c’est à dire soumis à aucune force de la part
, possède un mouvement rectiligne uniforme (ou un état de
. Tout référentiel en translation rectiligne et uniforme par
réalise un excellent référentiel galiléen. Ce référentiel a
pour origine le centre de masse du système solaire ( assimilable au centre du soleil ), les trois
axes se dirigent vers trois étoiles très éloignées et considérées comme fixes par r
apport à notre
a pour origine le centre d’inertie du soleil.
: centre de la terre, les trois axes sont identiques
aux axes précédemment définis ) est en translation elliptique ( quasi circulaire par rapport à
Il n'est donc pas rigoureusement galiléen, mais il sera considéré comme galiléen pour des
ces dont la durée est faible devant une année ( période de révolution de la terre autour
du soleil ) et dont les déplacements sont faibles devant la dimension de l'orbite terrestre.

Lycée Viette TSI 1
Rabeux Michel Page 5
Le référentiel terrestre ( ou référentiel de laboratoire ) ℜ
T
est lié à la terre, il est donc en
rotation autour du référentiel géocentrique. Il sera considéré comme galiléen pour des expé-
riences de faibles durées devant la période de rotation de terre autour d'elle même ( 86164 s )
et pour des déplacements faibles devant le rayon de la terre.
2. La deuxième loi de Newton : principe fondamental de la dynamique
Enoncé Par rapport à tout référentiel galiléen ℜ
ℜℜ
ℜ
g
, l’accélération d’un point matériel 
est proportionnelle à la résultante  des forces qui agissent sur . La
constante de proportionnalité est  la masse d’inertie du point matériel .
La propriété qu'a la masse d'intervenir dans cette relation s'appelle l'inertie.
Elle caractérise la difficulté à modifier la vitesse d’un point matériel soumis à une action
donnée.
L'unité de la masse est le kilogramme (  ). La masse est une grandeur additive et
conservative.
La masse d’inertie est identique à la masse gravitationnelle (postulat de la relativité générale)
Par la suite ces deux masses ( d’inertie et gravitationnelle ) seront nommées masses
En mécanique newtonienne, la masse est invariable par changement de référentiel.