Energétique du point matériel en référentiel galiléen

Energétique+du+point+matériel+
en+référentiel+galiléen+
+
I. Théorème+de+l’énergie+cinétique+
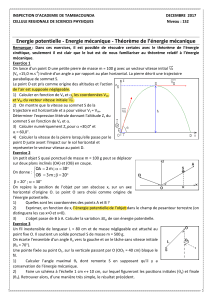
Exercice+1+:+Distance+d’arrêt+
!"# $%&"'# ()'*+&,-# M#.,# ()//,# 𝑚#,/'# -012*# /)"/# 3&',//,# &"&'&)-,# .,$4&/# 4"# $%&"'# 𝐴!#,'# 5-&//,# /)"/#
6+%'',(,"'/#/4+#4"#$-)"#&"1-&"*#74/849:#4"#$%&"'#𝐴!.#
;-#$%4+/4&'#,"/4&',#/)#1%4+/,#/4+#4"#$-)"#2%+&<%"')-#%=#&-#/4>&'#4",#6%+1,#.,#6+%'',(,"'/#𝐹!#.,#"%+(,#?#
𝐹=𝐹!=𝑓𝑚𝑔#
%=#𝑓#,/'#4"#1%,66&1&,"'#.,#6+%'',(,"'/#1%"/')"'#$%/&'&6@#
A&")-,(,"'B#-,#$%&"'#C#/9&((%>&-&/,#)4#$%&"'#𝐴!.#
D,# +*6*+,"'&,-# .4# -)>%+)'%&+,# ℛB# )//%1&*# )4# +,$E+,#.9,/$)1,# 1)+'*/&,"#𝑂,𝑒!,𝑒!,𝑒!B# ,/'# /4$$%/*#
5)-&-*,"@#
F)-14-,+#-)#.&/')"1,#.9)++G'#𝐷=𝐴!𝐴!@#
#
Exercice+2+:+Mouvements+de+glissement+
H"#1%"/&.E+,#4",#>&--,#MB#.,#()//,#𝑚B#/4/1,$'&>-,#.,#5-&//,+#?#
I#/%&'#/)"/#6+%'',(,"'#:#-9&"'*+&,4+#.94",#$%+'&%"#.,#7)"',#1&+14-)&+,#J84)+'#.,#1,+1-,#.,#+)K%"#RL#
I#/%&'#,"#$+*/,"1,#.,#6+%'',(,"'#/%-&.,B#*84&3)-,"'#:#4",#6%+1,#.,#"%+(,#𝑅!=𝑅!=−𝑓𝑅!B#/4+#4"#
$-)"#&"1-&"*#.9)"5-,#𝛼@#
#
M*',+(&",+#.)"/#12)84,#1)/#-)#3&',//,#(&"&()-,#𝑣!#849&-#6)4'#1%((4"&84,+#:#-)#>&--,#,"#𝑀!#$%4+#
849,--,#)'',&5",#-,#$%&"'#𝑀!@#

II. Théorème+de+l’énergie+mécanique+C+Intégrale+première+du+mouvement+
Exercice+3+:+Intégrale+première+du+mouvement+C+Positions+d’équilibre+
!"#$%&"'#()'*+&,-#M#.,#()//,#𝑚#5-&//,#/)"/#6+%'',(,"'#/4+#
4"#)N,#2%+&<%"')-!𝑂𝑥 .#F,#$%&"'#()'*+&,-#,/'#)11+%12*#:#4"#
+,//%+'# .,# 1%"/')"',# .,# +)&.,4+# 𝑘>0#,'#.,# -%"54,4+# :#
3&.,!𝑙!@#D9)4'+,#,N'+*(&'*#.4#+,//%+'#,/'#)'')12*#,"#4"#$%&"'#
H#',-#84,#𝑂𝐻 =ℎ<𝑙!.#
D,# +*6*+,"'&,-# .9*'4.,!ℛ!)//%1&*# )4# +,$E+,# .9,/$)1,#
1)+'*/&,"#,/'#/4$$%/*#5)-&-*,"@#
O#-9&"/')"'#&"&'&)-B#%"#-012,#-,#$%&"'#C#/)"/#3&',//,#:#$)+'&+#
.94"#$%&"'#/&'4*#:#-9)>/1&//,#𝑥!<𝑙!.#
#
PL F)-14-,+#-9*",+5&,#$%',"'&,--,#)//%1&*,#:#-)#+*/4-')"',#.,/#6%+1,/#84&#/9,N,+1,"'#/4+#M@#
QL R"# )$$-&84)"'# -,# '2*%+E(,# .,# -9*",+5&,# (*1)"&84,B# .*',+(&",+# -9&"'*5+)-,# $+,(&E+,# .4#
(%43,(,"'#.,#M@#
SL T,'+%43,+#1,'',#,N$+,//&%"#:#$)+'&+#.4#$+&"1&$,#6%".)(,"')-#.,#-)#.K")(&84,@#
UL R"#4'&-&/)"'#-9,N$+,//&%"#.,#-9*",+5&,#$%',"'&,--,B#.*',+(&",+#-,/#$%/&'&%"/#.9*84&-&>+,# .,#M#,'#
-,4+#/')>&-&'*@#
Exercice+4+:+Bille+dans+une+cuvette+
!",# >&--,#M#.,# ()//,# 𝑚#,/'# )11+%12*,# :# -9,N'+*(&'*# .94"#
*-)/'&84,# MBA#.,# 1%"/')"',# .,# +)&.,4+# 𝑘>0!,'# .,#
-%"54,4+#)4#+,$%/!𝑙!=𝐴𝐵@#
D)# >&--,# +%4-,# .)"/# 4",# 143,'',# )K)"'# -)# 6%+(,# .94"# 84)+'#
.,#/$2E+,#.,#+)K%"#R.&
H"# ",# /9&"'*+,//,+)# 849:# 4"# (%43,(,"'# $-)"# .,&M& ,'# %"#
"*5-&5,+)#'%4'#6+%'',(,"'#,"#M&,'#,"&B@#
D,#+*6*+,"'&,-#.9*'4.,# ℛ!)//%1&*#:#-)#143,'',#/,+)#/4$$%/*#
5)-&-*,"@#
D)#6%+1,#.,#+)$$,-#.,#-9*-)/'&84,#,/'#.,#-)#6%+(,#?#
𝑓=−𝑘𝐵𝑀#
#
#
#
O#-9&"/')"'#&"&'&)-B#%"#-012,#-)#>&--,#/)"/#3&',//,#&"&'&)-,#:#$)+'&+#.,#-)#$%/&'&%"#𝜃=𝜋/2.#
PL F)-14-,+#-9*",+5&,#$%',"'&,--,#)//%1&*,#:#-)#+*/4-')"',#.,/#6%+1,/#84&#/9,N,+1,"'#/4+#M@#
QL R"# )$$-&84)"'# -,# '2*%+E(,# .,# -9*",+5&,# (*1)"&84,B# .*',+(&",+# -9&"'*5+)-,# $+,(&E+,# .4#
(%43,(,"'#.,#M@#
SL T,'+%43,+#1,'',#,N$+,//&%"#:#$)+'&+#.4#$+&"1&$,#6%".)(,"')-#.,#-)#.K")(&84,@#
UL R"#4'&-&/)"'#-9,N$+,//&%"#.,#-9*",+5&,#$%',"'&,--,B#.*',+(&",+#-,/#$%/&'&%"/#.9*84&-&>+,# .,#M#,'#
-,4+#/')>&-&'*@#