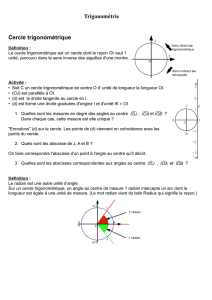
(Partie 1) - Trigonométrie

Séquence 4
ère
1
partie :
Dérivation (1)
e
2
partie :
Trigonométrie
Séquence 4 – MA12
1
© Cned - Académie en ligne
ère
1
partie
Dérivation (1)
Sommaire
1. Pré-requis
2. Nombre dérivé d’une fonction en un point
3. Fonction dérivée, exemples des fonctions de référence
4. Dérivation : opérations sur les fonctions
5. Premières applications de la dérivation
6. Synthèse de la partie 1 de la séquence
7. Exercices d’approfondissement
2
© Cned - Académie en ligne
Séquence 4 – MA12
1 Pré-requis
A
Les droites
Dans les graphiques de cette partie 1 de la Séquence 4, on utilise des droites non
parallèles à l’axe des ordonnées. On utilisera les équations réduites des droites
(c’est-à-dire de la forme y = mx + p ).
Les propriétés concernant le cœfﬁcient directeur m sont très utilisées.
Propriété
Si une droite, non parallèle à l’axe des ordonnées, passe par les points A et B dont les coordonnées
y −y
sont A x A ; y A et B x B ; y B , alors le cœfﬁcient directeur de la droite est : m = B A .
xB − x A
)
(
)
(
Propriété
Si une droite (non parallèle à l’axe des ordonnées) a pour cœfﬁcient directeur m l’un de ses
vecteurs directeurs est le vecteur u de coordonnées : u (1; m .
)
Il est très utile de savoir lire graphiquement un cœfﬁcient directeur, de voir
s’il est positif ou négatif, et de savoir comparer visuellement deux cœfﬁcients
directeurs.
Lecture
graphique
Sur la ﬁgure ci-contre, d’après l’inclinaison des droites (D) et
(D'), le cœfﬁcient m ' est positif, le cœfﬁcient m est négatif.
Et plus précisément m ' = 3 et m = −1.
1
m
(D’)
Quant à la droite (D") son cœfﬁcient directeur m " est
positif et m " < m ' car la droite (D") est « plus horizontale »
que la droite (D').
(D)
j
0
m’
i
Pour trouver le cœfﬁcient directeur m " , on cherche deux
points de la droite (D") ayant des coordonnées entières.
1
(D”)
B
3
A
5
On trouve les points A et B. On en déduit la lecture des
valeurs 5 et 3 comme cela est indiqué sur la ﬁgure, le
3
cœfﬁcient directeur est donc m " = (ce résultat vient de
5
yB − y A
).
l’égalité : m " =
xB − x A
Séquence 4 – MA12
3
© Cned - Académie en ligne
Équation d’une droite connaissant un point et le cœfficient directeur.
Propriété
On considère une droite (D) non parallèle à l’axe des ordonnées, d’équation
réduite y = mx + p.
Soit A( x A ; y A ) un point de cette droite.
On a alors y A = mx A + p , donc p = y A − mx A , et l’équation réduite de la
(
)
droite (D) devient y = mx + y A − mx A , c’est-à-dire y = m x − x A + y A .
Exemple
On considère la droite (D") de la ﬁgure précédente, passant par le point
3
A( −2 ; −6 ) et de cœfﬁcient directeur m " = .
5
3
3
24
Son équation réduite est y = ( x − ( −2)) + ( −6 ), soit y = x − .
5
5
5
B
Utilisation de GeoGebra
Tracé d’une courbe : par exemple, on tape y = x 2 sur la ligne de saisie, et,
quand on valide, la courbe s’afﬁche.
Création d’un point dont on connaît les coordonnées : on crée le point A
d’abscisse 1,5 et d’ordonnée 1, 52 en entrant (1.5,1.52 ) sur la ligne de saisie : il
faut faire attention aux points et à la virgule… !
Agrandissement : pour cela, il sufﬁt d’utiliser la roulette de la souris ou
l’agrandissement qui est une des fonctionnalités du bouton situé en haut à
droite ou encore en faisant un clic droit et en choisissant le pourcentage du
zoom.
Création d’un point mobile sur une courbe : il sufﬁt d’approcher
la souris de la courbe avant de cliquer pour créer un point B
sur la courbe (fonctionnalité du deuxième bouton en haut à
gauche).
Afﬁchage du cœfﬁcient directeur d’une droite : quand on crée
une droite, une équation s’afﬁche à gauche. S’il ne s’agit pas
de la forme réduite celle-ci peut être obtenue en faisant un clic
droit sur l’équation afﬁchée. On peut alors lire le cœfﬁcient
directeur.
y = x2
B
1,52
A
j
0
4
© Cned - Académie en ligne
i a = 1,5
Séquence 4 – MA12
C
Tableau de valeurs
Dans une des activités, un tableau de valeurs est demandé mais on ne peut
pas utiliser de façon habituelle les calculatrices car les valeurs de x ne sont pas
régulièrement espacées, il n’y a pas de « pas ».
Prenons l’exemple simple de la fonction carré et du tableau :
x
0
0,5
1
2
5
10
x2
Avec un tableur
On remplit 6 cellules d’une ligne (ou d’une colonne) par les valeurs de x.
On calcule le carré de 0 (en utilisant le nom de la cellule qui contient 0) dans
la première cellule de la ligne (ou la colonne) suivante, puis on recopie pour
obtenir les autres carrés.
Avec une calculatrice TI
On rentre la fonction carré dans Y1.
Dans TBLSET ( ou def table), on sélectionne Ask (ou Dem ), les calculs de
valeurs sont alors faits « à la demande » c’est-à-dire que l’on peut entrer les
valeurs de x que l’on veut dans la table.
Avec une calculatrice Casio
Ces calculatrices, sauf la Graph25+
Pro et la Graph35+, disposent d’un
tableur qu’on utilise avec le mode
S*SHT.
Pour la Graph25+ Pro et la Graph35+,
on peut utiliser les listes.
On rentre les valeurs de x dans List 1.
Pour calculer les carrés dans la colonne suivante, on se déplace avec le curseur et
on met en surbrillance List 2 en haut de la deuxième colonne. On rentre ensuite
la formule de la fonction dans laquelle on remplace x par List 1 qu’on obtient par
OPTN, List, encore List et 1. En validant, on obtient les valeurs attendues.
Séquence 4 – MA12
5
© Cned - Académie en ligne
2
Nombre dérivé
d’une fonction en un point
A
Activités
1. Activité 1
Avec une calculatrice ou un logiciel, afﬁcher la courbe représentative de la
fonction carré sur l’intervalle  −3 ; 3  .
Faire ensuite plusieurs agrandissements successifs centrés au point A de la
courbe, d’abscisse a = 1, 5.
Pour cela, avec une calculatrice, on peut changer la fenêtre ou utiliser un zoom
(zoom in pour une calculatrice Casio, zoom+ pour une calculatrice TI). Pour le
logiciel GeoGebra, voir les pré-requis.
Qu’observe-t-on ?
Avec un logiciel de géométrie construire la ﬁgure ci-contre.
y = x2
Le point A est sur la courbe et son abscisse est 1,5.
B
1,52
Le point B est un point mobile de la courbe. Comme on utilise
la droite (AB), le point B sera toujours différent de A.
A
Observer l’évolution du cœfﬁcient directeur de la droite (AB)
quand le point B se rapproche du point A (on dit que la droite
(AB) est une sécante en A à la courbe).
j
0
i a = 1,5
Les coordonnées du point A sont (1, 5 ; 1, 52 ). Les coordonnées du point B sont
( x ; x ) avec x ≠ 1,5.
2
Déterminer le cœfﬁcient directeur de la droite (AB) en fonction de x.
Avec un tableur ou une calculatrice, ou même ici en calculant mentalement,
déterminer les valeurs de ce cœfﬁcient pour les différentes valeurs de x du
tableau.
x
Cœfﬁcient directeur
x
Cœfﬁcient directeur
1
1,3
1,4
1,5001 1,5005 1,501
1,45
1,49
1,495
1,499
1,4995
1,4999
1,505
1,51
1,55
1,6
1,7
1,8
Pour mieux indiquer que l’étude faite ici est locale, autour du point A d’abscisse
1,5, on appelle 1, 5 + h l’abscisse du point B avec h ≠ 0, c’est-à-dire qu’on pose
x = 1, 5 + h. Comment exprimer que le point B se rapproche du point A ?
Quelle est l’ordonnée du point B en fonction de h ? Quelle est l’expression du
cœfﬁcient directeur de la droite (AB) en fonction de h ?
6
© Cned - Académie en ligne
Séquence 4 – MA12
Afﬁcher dans le tableau ci-dessous les valeurs de ce cœfﬁcient directeur lorsque
h prend des valeurs de plus en plus proches de 0 (strictement positives et
strictement négatives).
h
Cœfﬁcient directeur
h
Cœfﬁcient directeur
–1
–0,5
–0,1
–0,01
–0,001
–0,0001
0,00001
0,0001
0,001
0,01
0,1
1
Qu’observe-t-on ?
Quel semble être le cœfﬁcient directeur de la droite qui est apparue à la
question ? Pour terminer cette activité, on peut tracer cette droite sur le
graphique (on sait aussi qu’elle passe par le point A).
2. Activité 2
On considère la fonction f déﬁnie sur par f ( x ) =
1
et on choisit a = 1.
x2 +1
Reprendre les questions , , en admettant que le taux d’accroissement en
−1− 0, 5h
fonction de h est égal à
, et ﬁnir par la question .
2 + 2h + h 2
3. Activité 3
Reprendre la question dans le cas suivant :
f est la fonction déﬁnie sur par f ( x ) = x 2 − 1 et a = 1(avec le logiciel
GeoGebra la valeur absolue s’obtient en saisissant abs( x 2 − 1) ).
4. Activité 4
Reprendre les questions , , dans le cas de la fonction racine carrée avec
a = 0. C’est donc l’origine O du repère qui joue le rôle du point A des activités
précédentes. On tiendra compte de l’ensemble de déﬁnition de la fonction racine
carrée, l’abscisse du point B sera donc un nombre h strictement positif.
Quelle est ici la droite « limite » des droites sécantes (OB) ?
B
Cours
1. Introduction
Dans cette séquence on introduit un nouvel outil dans le cours de mathématiques :
la dérivation.
Séquence 4 – MA12
7
© Cned - Académie en ligne
Les coordonnées commencent à être utilisées en mathématiques à partir de
1637 grâce à Descartes (d’où l’adjectif « cartésien ») et à Fermat. Vers 1680,
Newton et Leibniz créent le calcul différentiel (autre nom de ce qui deviendra la
dérivation) qui permet d’étudier les tangentes à une courbe moins simple que
le cercle ou la parabole, de travailler avec la notion de vitesse instantanée et
d’aborder des calculs avec des différences qui deviennent très proches de 0
(h = x − a dans nos exemples ci-dessus).
L’acquisition du concept de dérivée est un point fondamental du programme de
première S.
Les activités précédentes permettent une approche intuitive de cette notion :
une fonction est dérivable en a lorsque sa courbe représentative semble
confondue avec une droite non parallèle à l’axe des ordonnées lorsqu’on agrandit
sufﬁsamment cette courbe autour de son point d’abscisse a.
La mise en forme rigoureuse est très délicate, mais l’essentiel est d’avoir compris
l’idée, en particulier d’avoir une image mentale de la « droite limite » des
sécantes en un point, la tangente en ce point. Donc, dans le cours de Première S,
on se contentera d’un point de vue intuitif en ce qui concerne la déﬁnition de la
dérivabilité et de la limite qui intervient dans cette déﬁnition.
Ce premier chapitre est essentiellement formé des déﬁnitions fondamentales et
d’exemples.
2. Définitions fondamentales
Les activités ont montré dans plusieurs cas l’existence d’une « droite limite » des
sécantes (AB) en un point A à une courbe quand le point B se rapproche du point
A, en restant distinct de A.
Cette droite est déﬁnie par le point A et son cœfﬁcient directeur.
C’est l’existence et la valeur de ce cœfﬁcient directeur qui vont être à la base de
la notion de dérivabilité.
Soit f une fonction déﬁnie sur un intervalle I et soit a un
nombre réel appartenant à l’intervalle I.
B
A
a
8
© Cned - Académie en ligne
y = f(x)
j
a+h
0
Le point A est le point de la courbe d’abscisse a, ses
coordonnées sont (a ; f (a )).
Le point B est le point de la courbe d’abscisse a + h , ses
coordonnées sont (a + h ; f (a + h )).
Le point B est distinct du point A, donc h ≠ 0.
i
Séquence 4 – MA12
Le cœfﬁcient directeur de la droite (AB) est égal au quotient
yB − y A
f (a + h ) − f (a )
, c’est-à-dire
.
xB − x A
h
Définition 1
Soit f une fonction déﬁnie sur un intervalle I, a et a + h (h ≠ 0 ) deux
éléments de l’intervalle I.
f (a + h ) − f (a )
est appelé taux d’accroissement de la fonction
h
f entre a et a + h.
Le quotient
Définition 2
Soit f une fonction déﬁnie sur un intervalle I et soit a un nombre réel
appartenant à l’intervalle I.
f (a + h ) − f (a )
Si le taux d’accroissement
tend vers un nombre réel quand
h
h tend vers 0, on dit que la fonction f est dérivable en a.
Le nombre réel qui est la limite du taux d’accroissement quand h tend vers
0 est appelé le nombre dérivé de la fonction f en a, on le note f '(a ) et on
écrit :
f (a + h ) − f (a )
= f '(a ).
h
h →0
lim
Lecture
Le nombre f '(a ) se lit « f prime de a ».
La quantité lim
h →0
vers 0 ».
Commentaire
f (a + h ) − f (a )
f (a + h ) − f (a )
se lit « limite de
quand h tend
h
h
Il ne faut pas se laisser impressionner par cette déﬁnition qui est nécessaire pour
savoir de quoi on parle.
On l’utilisera pour quelques exemples. Puis les résultats obtenus dans les
chapitres 3 et 4 permettront d’éviter au maximum les calculs utilisant la limite du
taux d’accroissement de la déﬁnition 2.
Exemple 1
Montrer que la fonction carré est dérivable en a = 1, 5 et déterminer le nombre
dérivé correspondant.
Solution
Notons f la fonction carré. On étudie la dérivabilité en a = 1, 5 : on étudie donc le
2
2
f (a + h ) − f (a ) (1, 5 + h − 1, 5
taux d’accroissement
quand h ≠ 0.
=
h
h
Comme on étudie ce qui se passe quand h tend vers 0, c’est-à-dire quand le
dénominateur tend vers 0, le quotient sous cette forme ne nous donne aucun
renseignement. On va donc le transformer en développant puis en simpliﬁant.
)
2
1, 5 + h ) − 1, 52 (1, 5
(
On a :
=
2
h
)
+ 3h + h 2 − 1, 52
h
=
h( 3 + h )
= 3 + h avec h ≠ 0.
h
Séquence 4 – MA12
9
© Cned - Académie en ligne
Comme le taux d’accroissement est égal à 3 + h , il a pour limite 3 quand h tend
vers 0.
La fonction f, c’est-à-dire la fonction carré, est donc dérivable en 1,5 et f '(1, 5) = 3.
On retrouve heureusement le résultat conjecturé d’après les tableaux de valeurs
dans l’activité 1.
Exemple 2
Montrer que la fonction racine carrée est dérivable en a = 1 et déterminer le
nombre dérivé correspondant.
Solution
Notons f la fonction racine carrée. On étudie la dérivabilité en a = 1, on étudie
f (a + h ) − f (a )
1+ h − 1
=
quand la racine
h
h
existe et que h n’est pas nul, c’est-à-dire pour h ≥ −1et h ≠ 0.
donc le taux d’accroissement
Comme on étudie ce qui se passe quand h tend vers 0, c’est-à-dire quand le
dénominateur tend vers 0, le quotient sous cette forme ne nous donne aucun
renseignement. On va donc le transformer en utilisant la quantité conjuguée du
numérateur (voir la Partie 1 de la Séquence 1).
On a :
1+ h − 1
=
h
(
)(
1+ h − 1
h
car on a pu simpliﬁer par h.
(
)=
1+ h + 1
)
1+ h + 1
h
(
(1+ h ) − 1
)
1+ h + 1
=
1
1+ h + 1
Sous cette forme, quand h tend vers 0, on obtient intuitivement que 1+ h a pour
limite 1, que 1+ h a pour limite 1 , c’est-à-dire 1, que le dénominateur a pour
1
limite 2 et que le taux d’accroissement a donc pour limite .
2
On peut donc conclure que la fonction racine carrée est dérivable en 1 et que
1
f '(1) = .
2
Là encore, on retrouve bien le résultat conjecturé d’après les tableaux de valeurs
dans l’activité 4.
Exemple 3
Comme on l’a vu dans l’activité 4 la fonction racine carrée n’est pas dérivable
en 0.
Comme on l’a vu dans l’activité 3, la fonction f déﬁnie sur par f ( x ) = x 2 − 1
n’est pas dérivable en 1, il en est de même pour la fonction valeur absolue en 0.
Remarque
L’exemple de l’exercice I du chapitre 7 (approfondissement) ci-après, permet
de voir à quoi peut ressembler la courbe d’une fonction non dérivable en une
valeur a. Ces exemples sont donnés seulement pour mieux comprendre, par
comparaison, ce qu’est une fonction dérivable en un point.
Toutes les fonctions étudiées dans les exercices seront « régulières », c’est-àdire dérivables en chaque valeur de leur ensemble de déﬁnition, sauf la fonction
racine et la fonction valeur absolue en 0.
10
© Cned - Académie en ligne
Séquence 4 – MA12
Définition 3
Soit a un nombre réel et f une fonction dérivable en a.
La tangente à la courbe représentative de f au point d’abscisse a est la
droite passant par le point de la courbe de coordonnées (a ; f (a )) et ayant
pour cœfﬁcient directeur f '(a ), le nombre dérivé en a.
Commentaire
La déﬁnition 3 permet de lire des nombres dérivés sur des graphiques.
En effet, si la courbe représentative d’une
fonction f est dessinée ainsi que la tangente en
un point A d’abscisse a de la courbe, on peut lire
le nombre dérivé en a puisque c’est le cœfﬁcient
directeur de la tangente en A.
A
4
puisque l’abscisse
3
du point A est égale à 9 et que le cœfﬁcient
4
directeur de la tangente est égal à (voir les
3
pré-requis).
Ci-contre, on lit f '(9 ) =
j
0
i
Remarque
Il se peut que la fonction ne soit pas dérivable en a et qu’il existe néanmoins
une tangente à la courbe représentative au point d’abscisse a. C’est le cas de la
fonction racine en a = 0 et de sa courbe à l’origine O : c’est l’axe des ordonnées
qui est la tangente et cet axe n’a pas de cœfﬁcient directeur.
Propriété 1
Soit a un nombre réel et f une fonction dérivable en a.
La tangente à la courbe représentative de f au point d’abscisse a est la
droite qui a pour équation
y = f '(a )( x − a ) + f (a ).
Démonstration
Remarque
On a simplement appliqué la propriété rappelée dans les pré-requis.
La notion de dérivabilité et la notion tangente sont des notions locales.
Dans les activités, on a zoomé autour d’un point de la courbe en ne voyant plus
le reste de la courbe.
Et, quand on observe les tangentes dessinées à la ﬁn des activités 1 et 2, on
constate bien que, en dehors du voisinage du point de tangence, la tangente n’a
pas de rôle particulier par rapport à la courbe.
Séquence 4 – MA12
11
© Cned - Académie en ligne
Exemple 4
Dans l’activité 1, la tangente à la courbe
représentative de la fonction carré au point
A d’abscisse 1,5 est la droite passant par le
point A et dont le cœfﬁcient directeur est
égal à 3.
A
D’après la propriété 1, cette tangente a
pour équation y = f '(1, 5)( x − 1, 5) + f (1, 5),
soit y = 3( x − 1, 5) + 2, 25
c’est-à-dire y = 3x − 2, 25.
j
0
i
Comme il s’agit d’une notion locale, autour du point A, on a tracé seulement une
partie de la droite au voisinage de point A.
Exemple 5
Dans l’activité 2, la tangente à la courbe représentative de la fonction déﬁnie sur
1
au point A d’abscisse 1 est la droite
par f ( x ) =
x2 +1
passant par le point A et dont le cœfﬁcient directeur est
égal à
A
−0, 5.
Cette tangente a pour équation :
j
0
y = f '(1)( x − 1) + f (1), soit y = −0, 5( x − 1) + 0, 5 c’est-à-dire
i
y = −0, 5x + 1.
Les déﬁnitions de la dérivabilité d’une fonction f en a et de la tangente à la courbe
représentative de f au point A d’abscisse a donnent un moyen pour calculer des
valeurs approchées de f ( x ) lorsque x est proche de la valeur a.
En effet, comme la courbe d’équation y = f ( x ) est presque confondue avec
sa tangente au voisinage du point A, les valeurs f ( x ) seront très proches des
valeurs obtenues à partir de la fonction afﬁne représentée par la droite tangente
d’équation y = f '(a )( x − a ) + f (a ).
Définition 4
Soit f une fonction déﬁnie sur un intervalle I et soit a un nombre réel
appartenant à l’intervalle I.
Si la fonction f est dérivable en a, on dit que la fonction afﬁne
x → f '(a )( x − a ) + f (a ) est l’approximation afﬁne de f en a.
Commentaire
Au voisinage du point A, la courbe et la
tangente en A sont presque confondues,
on peut donc écrire que f '(a )( x − a ) + f (a )
est une valeur approchée de f ( x ) :
f ( x ) ≈ f '(a )( x − a ) + f (a ).
y=f(a)(x–a)+f(a)
f(x)
f ’(a)(x–a)+f(a)
j
0
12
© Cned - Académie en ligne
Séquence 4 – MA12
A
f(a)
i
a x
Remarque
Toute droite passant par A permettrait aussi de donner un moyen d’approcher
les valeurs f ( x ) de façon afﬁne mais moins précise. Etant donnée la position
exceptionnelle de la tangente en A par rapport à la courbe, on utilise seulement
la fonction afﬁne x → f '(a )( x − a ) + f (a ).
Exemple 6
On rappelle que, dans l’exemple 4, on a vu que la tangente à la courbe
représentative de la fonction carré au point A d’abscisse 1,5 est la droite
d’équation y = f '(1, 5)( x − 1, 5) + f (1, 5), soit y = 3x − 2, 25.
x
3x − 2, 25
x2
1,45
1,46
1,47
1,48
1,49
1,5
1,51
1,52
1,53
1,54
1,55
2,1
2,13
2,16
2,19
2,22
2,25
2,28
2,31
2,34
2,37
2,4
2,1025
2,1316
2,1609
2,1904
2,2201
2,25
2,2801
2,3104
2,3409
2,3716
2,4025
On obtient donc f ( x ) ≈ 3x − 2, 25 c’est-à-dire
x 2 ≈ 3x − 2, 25 lorsque x est proche de 1,5.
Ainsi, on trouve 1, 50022 ≈ 3 × 1, 5002 − 2, 25 soit
1, 50022 ≈ 2, 2506, alors que la valeur exacte est
1, 50022 = 2, 25060004.
Dans le tableau de valeurs ci-contre, on a aussi
indiqué les valeurs exactes dans la troisième colonne
pour montrer la précision des approximations.
Remarque
f(a+h)
f(a)+f ’(a) h
f ’(a) h
A
f(a)
h
y=f(x)
j
0
i
a
a+h
Le cœfficient directeur est f’(a)
En posant x = a + h l’approximation f ( x ) ≈ f '(a )( x − a ) + f (a ) devient
f (a + h ) ≈ f '(a ) × h + f (a ) qu’on écrit plutôt sous la forme
f (a + h ) ≈ f (a ) + f '(a ) × h.
Cette nouvelle expression montre mieux comment les valeurs approchées sont
construites à partir de f (a ) comme on l’observe sur la ﬁgure.
Quand la variable augmente de la valeur h, on obtient une valeur approchée de
l’image f (a + h ) en ajoutant le produit f '(a ) × h à l’image f (a ).
Séquence 4 – MA12
13
© Cned - Académie en ligne
Exemple 7
C’est toujours le même exemple mais avec ce nouveau point de vue.
2, 25 + 3h (1, 5 + h )2
h
-0,005
-0,004
-0,003
-0,002
-0,001
0
0,001
0,002
0,003
0,004
0,005
2,235
2,238
2,241
2,244
2,247
2,25
2,253
2,256
2,259
2,262
2,265
C
2,235025
2,238016
2,241009
2,244004
2,247001
2,25
2,253001
2,256004
2,259009
2,262016
2,265025
Il s’agit donc de la fonction carré et
a = 1, 5, f (a ) = 2, 25, f '(a ) = 3.
Dans ce cas, l’approximation f (a + h ) ≈ f '(a ) × h + f (a ) devient
donc (1, 5 + h )2 ≈ 2, 25 + 3h le nombre h étant proche de 0.
Ainsi, en reprenant le calcul de l’exemple 6 :
1, 50022 = (1, 5 + 0, 0002)2 d’où :
(1, 5 + 0, 0002)2 ≈ 2, 25 + 3 × 0, 0002 soit 1, 50022 ≈ 2, 2506.
Pour ce tableau de valeurs, on a choisi de partir de la valeur
a + h = 1, 5 − 0, 005, soit h = −0, 005 et d’utiliser 0,001 pour
le pas.
On a encore indiqué les valeurs exactes pour montrer la
précision des approximations.
Exercices d’apprentissage
Exercice 1
On donne ci-contre la courbe représentative d’une fonction f déﬁnie et dérivable
sur .
Parmi les réponses proposées, cocher celles qui sont correctes.
A
Une valeur approchée de f '( 4 ) est :
5/4 –5/4 9/5 5/9
9/5 4/5 –5/9 –9/5
B
La droite (D) est tangente à courbe :
j
0
oui non
i
La droite (AB) est tangente à la courbe
(D)
au point A : oui non
au point B : oui non
Combien y a-t-il de nombres dérivés nuls :
y=f(x)
01 23
Exercice 2
On donne ci-après la courbe représentative d’une fonction f déﬁnie sur .
Tracer les tangentes aux points A, B, C, D de la courbe représentative de f,
d’abscisses respectives −2, − 1, 0 et 1. Donner des valeurs approchées des
nombres dérivés de la fonction f en −2, − 1, 0 et 1.
14
© Cned - Académie en ligne
Séquence 4 – MA12
j
0
Exercice 3
i
Soit une fonction f déﬁnie sur . En utilisant le tableau suivant, placer six
points de la courbe (Cf ) représentative de f et tracer la tangente à la courbe
(Cf ) en chacun de ces points.
x
–3
–2
0
0,5
2
3
f (x)
1
0,75
1,75
2
–– 2
2
f’ (x)
– 0,5
0
1
0
0
8
On donne aussi le tableau de variation, tracer alors l’allure de la courbe (C ).
f
x
−∞
−2
2
+∞
2
f (x )
0,75
Exercice 4
0,5
–2
Soit f la fonction déﬁnie sur par f ( x ) = 3x 2 − 5x + 8. Démontrer que la
fonction f est dérivable en a = 2 et donner la valeur de f '(2).
On note g la fonction inverse. Démontrer que la fonction inverse est dérivable
en a = 2 et donner la valeur de g '(2).
Exercice 5
Soit f une fonction dérivable en un réel a. Déterminer une équation de la
tangente à la courbe Cf , représentant la fonction f, au point A d’abscisse a
sachant que : a = 2, f '(a ) = −4 et f (a ) = 3.
Même question pour la fonction g avec a = 1, g '(a ) = −3 et la tangente passe
par l’origine du repère.
Même question pour la fonction h avec h '(a ) = 0 et h (a ) = 5.
Exercice 6
On a démontré dans le cours que la fonction racine carrée est dérivable en 1
1
et que son nombre dérivé en 1 est égal à . Donner une valeur approchée de
2
1, 000002 et de 0, 999999999 .
Séquence 4 – MA12
15
© Cned - Académie en ligne
Exercice 7
Représenter la fonction carré, la fonction inverse et la fonction racine carrée
dans un même repère orthonormé.
Soit a un nombre réel strictement supérieur à 1 et m le nombre dérivée en
a d’une de ces fonctions. Le nombre m est donc le cœfﬁcient directeur de la
tangente à l’une des courbes, au point d’abscisse a, a > 1.
En utilisant les représentations graphiques, cocher dans chaque cas la bonne
réponse parmi les 4 :
Valeur de m
C’est impossible
Il s’agit de la fonction
carré
inverse
racine carrée
m=3
m=1
m = 0,4
m=0
m = –0,5
m = –4
Quelles conjectures, exprimées par des inégalités, peut-on faire sur les nombres
dérivés en a, avec a > 1, pour chacune des trois fonctions ?
16
© Cned - Académie en ligne
Séquence 4 – MA12
3
A
Fonction dérivée, exemples
des fonctions de référence
Activités
1. Activité 1
On a étudié la dérivabilité de la fonction carré en a = 1, 5 dans l’exemple 1 dans
le chapitre précédent.
On demande ici d’étudier la dérivabilité en a, a étant un nombre réel ﬁxé.
2. Activité 2
Étudier la dérivabilité de la fonction cube en a = 2.
On utilisera l’identité remarquable : (a + b )3 = a 3 + 3a 2b + 3ab 2 + b 3
(ce qui se démontre en développant
(a + b )3 = (a + b )2 × (a + b ) = (a 2 + 2ab + b 2 )(a + b ) = ...).
Soit a un nombre réel, étudier la dérivabilité de la fonction cube en a.
3. Activité 3
Dans l’exercice 4, on a étudié la dérivabilité de la fonction inverse en a = 2.
On demande ici d’étudier la dérivabilité de la fonction inverse en a, a étant un
nombre réel non nul.
B
Cours
1. Définition
Exemple 8
Notation
Dans l’activité 1, on a montré que la fonction carré est dérivable en a quelque soit
le nombre réel a et que, si on note f la fonction carré, on a f '(a ) = 2a.
On peut donc considérer la nouvelle fonction déﬁnie sur par a → 2a , ou
encore a → f '(a ).
Puisque, dans la ligne précédente, a est une variable, on peut utiliser le nom
habituel d’une variable et on obtient la fonction déﬁnie sur par : x → f '( x )
avec f '( x ) = 2x .
Définition 5
On dit qu’une fonction f est dérivable sur un intervalle I si f est déﬁnie sur I
et dérivable en tout point de l’intervalle I.
La fonction, déﬁnie sur l’intervalle I et à valeurs dans , qui à tout réel x de
l’intervalle I associe le nombre dérivé de f en x est appelée fonction dérivée
de f ; cette fonction dérivée est notée f '.
Séquence 4 – MA12
17
© Cned - Académie en ligne
Exemple 9
Dans l’activité 2, on a montré que la fonction cube est dérivable sur et, en
notant f la fonction cube, la fonction dérivée de la fonction cube est déﬁnie sur
par f '( x ) = 3x 2.
De même, dans l’activité 3, on a montré que la fonction inverse est dérivable sur
 −∞ ; 0  ∪ 0 ; + ∞  et, en notant f la fonction inverse, la fonction dérivée de
−1
la fonction inverse est déﬁnie sur  −∞ ; 0  ∪ 0 ; + ∞ par f '( x ) = .
x2
2. Fonctions dérivées des fonctions de référence
Propriété 2 : Résultats à connaître parfaitement
Fonctions
Fonctions dérivées
Les fonctions constantes
f :→
x →k
Les fonctions constantes sont déﬁnies et f ': → dérivables sur .
x →0
Les fonctions afﬁnes
f :→
x → mx + p
Les fonctions afﬁnes sont déﬁnies et f ': → dérivables sur .
x →m
La fonction carré
La fonction carré est déﬁnie et dérivable f ': → sur .
x → 2x
f :→
x → x2
Les fonctions puissances : Les fonctions puissances sont déﬁnies et f ': → soit n un entier naturel dérivables sur .
x → nx n −1
non nul
f :→
x → xn
La fonction inverse
f : * → x→
1
x
La fonction racine carrée
f : 0 ; + ∞  → x→ x
18
© Cned - Académie en ligne
Séquence 4 – MA12
La fonction inverse est déﬁnie et dérivable
f ': ∗ → sur  −∞ ; 0  ∪ 0 ; + ∞  .
−1
x→
x2
La fonction racine carrée est déﬁnie f ': 0 ; + ∞  → 

sur 0 ; + ∞ et dérivable seulement sur
1
x→
0 ; + ∞  .
2 x
Attention : la fonction racine carrée est
déﬁnie en 0 mais n’est pas dérivable en 0.
Remarque 1
La fonction valeur absolue n’apparaît pas dans ce tableau.
On a vu que la fonction valeur absolue n’est pas dérivable en 0, et d’ailleurs, si on
rencontre une valeur absolue, il est souvent plus commode de travailler sans la
valeur absolue en distinguant les deux cas suivant que la quantité dont on prend
la valeur absolue est positive ou négative.
En Première S, pour la dérivation, on restera dans des situations simples, sans
valeur absolue.
Remarque 2
On a expliqué plus haut le changement de notation du nom de la variable.
Mais ici, dans les démonstrations qui suivent, on utilise la déﬁnition 2 et on
revient à la notation a pour retrouver, dans ces calculs un peu désagréables, les
quantités familières a+h, f(a+h)… dans le taux d’accroissement.
Démonstration
Les fonctions constantes
Voir ci-dessous, car les fonctions constantes sont des cas particuliers des fonctions
afﬁnes, avec m = 0.
Les fonctions afﬁnes
Soit f une fonction afﬁne, elle est déﬁnie sur , et on a f ( x ) = mx + p , où m et
p sont des constantes.
On sait que la courbe Cf représentative de la fonction f est une droite, donc, bien
sûr, cette courbe Cf admet une tangente en tout point d’abscisse a, quelque soit
le nombre réel a : elle est sa propre tangente !
Et comme le cœfﬁcient directeur de la droite Cf d’équation y = mx + p est le
nombre m on peut en déduire que la fonction afﬁne f est dérivable en a, quel que
soit le nombre réel a, et que f '(a ) = m.
Autre point de vue : on peut raisonner en utilisant le taux d’accroissement et la
déﬁnition 2.
Pour la fonction afﬁne f, on a donc pour tout h ≠ 0 :
f (a + h ) − f (a ) m(a + h ) + p − (ma + p ) mh
=
=
= m et donc, bien sûr, puisque ce
h
h
h
quotient est égal au nombre constant m, on a aussi :
f (a + h ) − f (a )
lim
= lim m = m.
h
h →0
h →0
Donc la fonction afﬁne f est dérivable en a pour tout réel a, et f '(a ) = m.
La fonction carré
Le résultat est démontré dans le corrigé de l’activité 1.
Les fonctions puissances
Le résultat a été démontré pour n = 2 et n = 3 dans les activités 1 et 2.
En Première S, on admet le résultat pour les autres valeurs de n.
La fonction inverse
Le résultat est démontré dans le corrigé de l’activité 3.
Séquence 4 – MA12
19
© Cned - Académie en ligne
La fonction racine carrée
Soit g la fonction racine carrée, déﬁnie sur 0 ; + ∞ par g ( x ) = x .
Soit a un nombre réel strictement positif.
On écrit le taux d’accroissement et on le transforme en utilisant la quantité
conjuguée du numérateur (voir dans la partie 1 de la Séquence 1).
Pour tout h ≠ 0 on a :
g (a + h ) − g (a )
a +h − a
=
=
h
h
=
h
(
(a + h ) − a
a +h + a
(
a +h − a
h
)
=
(
)(
a +h + a
a +h + a
1
a +h + a
)
)
.
C’est ici que la condition a ≠ 0 doit être réalisée car elle est indispensable pour
obtenir un nombre réel en prenant la limite quand h tend vers 0.
f (a + h ) − f (a )
1
1
.
= lim
=
h
h →0
h →0 a + h + a 2 a
Donc la fonction racine est dérivable en a quelque soit a réel strictement positif
1
f '(a ) =
.
2 a
Donc : lim
Exemple 10
La
fonction afﬁne f déﬁnie sur par f ( x ) = 3x − 8 est dérivable sur et sa
fonction dérivée f ' est déﬁnie sur par f '( x ) = 3.
La
fonction afﬁne f déﬁnie sur par f ( x ) = −5x + 3 est dérivable sur et sa
fonction dérivée f ' est déﬁnie sur par f '( x ) = −5.
fonction puissance 5, notée f, déﬁnie sur par f ( x ) = x 5 est dérivable sur
et sa fonction dérivée f ' est déﬁnie sur par f '( x ) = 5x 4 .
La
Commentaire
C
Exercice 8
Dans le chapitre suivant, les théorèmes sur les opérations permettront de
déterminer les fonctions dérivées de très nombreuses fonctions fabriquées à
partir des fonctions de référence.
Exercices d’apprentissage
On considère la fonction puissance 7, déﬁnie et dérivable sur .
Quel est son nombre dérivé en 1 ? en 3 ? en 0 ? en −1?
On considère la fonction inverse, déﬁnie et dérivable sur  −∞ ; 0  ∪  0 ; + ∞  .
Quel est son nombre dérivé en 1 ? en 3 ? en −1? en −5 ?
20
© Cned - Académie en ligne
Séquence 4 – MA12
On considère la fonction racine carrée déﬁnie sur  0 ; + ∞ et dérivable sur
0 ; + ∞  .
Quel est son nombre dérivé en 1 ? en 3 ? en 0,25 ? en 0,49 ?
Exercice 9
Démontrer la propriété obtenue avec les représentations graphiques dans la
question de l’exercice 7 du chapitre 2.
Exercice 10
Soit (C) la courbe représentative de la fonction carré dans un repère orthogonal.
Déterminer le(s) point(s) où la tangente (T) à la courbe (C) est parallèle à la
droite (D) d’équation y = 4 x + 5.
Même question avec la droite (∆) d’équation y = − x + 3.
Faire une ﬁgure où l’on placera la courbe (C), les droites (D) et ( ∆ ), et les
tangentes trouvées aux questions précédentes.
Exercice 11
Soit (C) la courbe représentative de la fonction inverse dans un repère orthogonal.
Déterminer le(s) point(s) où la tangente (T) à la courbe (C) est parallèle à la
droite (D) d’équation y = −0, 25x + 3.
Même question en remplaçant (D) par la droite ()) tangente à la parabole
d’équation y = x 2 au point d’abscisse −1.
Faire une ﬁgure où l’on placera la courbe (C), les droites (D) et ()), et les
tangentes trouvées aux questions précédentes.
Séquence 4 – MA12
21
© Cned - Académie en ligne
4
A
Dérivation : opérations
sur les fonctions
Activités
1. Activité 1
On considère les fonction u et v déﬁnies sur par u ( x ) = 5x + 1 et v ( x ) = x 2.
On a vu précédemment que les fonctions u et v sont dérivables sur .
Donner les valeurs de u '( 3) et v '( 3).
On appelle f la fonction, déﬁnie sur , égale à la somme des deux fonctions
u et v : f = u + v .
En utilisant le taux d’accroissement de la fonction f en a et la déﬁnition 2,
démontrer que la fonction f est dérivable en a = 3.
Quelle est la valeur de f '( 3) ? Qu’observe-t-on ?
Généralisation : démontrer, en utilisant la déﬁnition 2, que la propriété
observée à la question est vraie pour toute fonction f telle que f = u + v ,
quelles que soient les fonctions u et v, et quelque soit le nombre réel a où les
deux fonctions u et v sont dérivables.
2. Activité 2
On considère les fonctions u et v déﬁnies sur par u ( x ) = 5x et v ( x ) = 0, 2x .
On a vu précédemment que les fonctions afﬁnes u et v sont dérivables sur .
Donner les valeurs de u '( 3) et v '( 3).
On appelle f la fonction, déﬁnie sur  0 ; + ∞  , égale au produit des deux
fonctions u et v : f = uv .
Quelle est la valeur de f '( 3) ? Qu’observe-t-on ?
B
Cours
1. Opérations
On connaît depuis le chapitre précédent les fonctions dérivées des fonctions de
référence.
À partir des fonctions de référence on peut fabriquer d’autres fonctions par
addition, multiplication, quotient comme on l’a vu dans partie 2 de la Séquence 2.
22
© Cned - Académie en ligne
Séquence 4 – MA12
Dans l’activité 1, on a vu que pour un exemple de fonction déﬁnie par une
addition tout se passe simplement, on a même démontré que cette propriété est
générale.
L’activité 2 a montré que, malheureusement, ce n’est pas aussi simple pour les
produits.
Et, de même, la fonction dérivée de la fonction inverse montre que les inverses, et
donc les quotients, ne se dériveront pas aussi aisément que les sommes.
Nous allons donner ici, puis démontrer, les formules qui permettent d’obtenir les
fonctions dérivées lorsqu’on utilise des opérations.
Propriété 3 : Résultats à connaître parfaitement
Ces résultats sont établis, bien sûr, là où les fonctions u et v sont déﬁnies et
dérivables, et là où le dénominateur ne s’annule pas pour les deux derniers
cas.
Démonstration
Somme
Fonction
Fonction dérivée
u +v
(u + v )' = u '+ v '
ku , k constante réelle
(ku )' = ku '
uv
(uv )' = u 'v + uv '
u2
(u 2 )' = 2u 'u
1
u
 1  −u '
 u  = 2
u
u
v
 u  u 'v − uv '
 v  =
v2
'
'
: voir le corrigé de l’activité1.
Produit
d’une fonction par un réel constant
On considère une fonction u déﬁnie et dérivable sur un intervalle I et soit a un
nombre de l’intervalle I.
Soit k un nombre réel.
On appelle f la fonction, déﬁnie sur I, égale au produit ku : f = ku .
Pour étudier la dérivabilité de la fonction f en a on calcule le taux
f (a + h ) − f (a )
d’accroissement
et on en cherche la limite éventuelle quand
h
h tend vers 0.
Séquence 4 – MA12
23
© Cned - Académie en ligne
On a :
f (a + h ) − f (a ) (ku )(a + h ) − (ku )(a )
=
h
h
k (u (a + h ) − u (a ))
=
h
u (a + h ) − u (a )
=k
.
h
)
)
Attention, l’écriture (ku (a + h n’est
pas l’écriture d’un produit.
C’est l’écriture de l’image du nombre
(a + h par la fonction (ku .
)
)
u (a + h ) − u (a )
f (a + h ) − f (a )
= u '(a ), donc lim
= ku '(a ).
h
h
h →0
h →0
Donc la fonction f = ku est dérivable en a et f '(a ) = ku '(a ).
On sait que lim
Cette propriété est vraie pour tout a de l’intervalle I et f = ku , on obtient donc :
(ku ' = ku '.
)
Produit de deux fonctions
On considère deux fonctions u et v déﬁnies et dérivables sur un intervalle I et soit
a un nombre de l’intervalle I.
On appelle f la fonction, déﬁnie sur I, égale au produit des deux fonctions u et
v : f = uv .
Pour étudier la dérivabilité de la fonction f en a on calcule le taux d’accroissement
f (a + h ) − f (a )
et on en cherche la limite éventuelle quand h tend vers 0.
h
f (a + h ) − f (a ) (uv )(a + h ) − (uv )(a )
=
h
h
u (a + h ) × v (a + h ) − u (a ) × v (a )
=
.
h
u (a + h ) − u (a )
v (a + h ) − v (a )
= u '(a ) et que lim
= v '(a ).
On sait que lim
h
h
h →0
h →0
On a :
f (a + h ) − f (a )
h
on soustrait et on ajoute la quantité u (a ) × v (a + h ) au numérateur, ce qui n’en
change pas la valeur. On obtient :
Pour pouvoir faire intervenir ces deux quotients dans le calcul de
f (a + h ) − f (a ) u (a + h ) × v (a + h ) − u (a ) × v (a + h ) + u (a ) × v (a + h ) − u (a ) × v (a )
=
h
h
u (a + h ) − u (a )
v (a + h ) − v (a )
v (a + h ) + u (a )
=
.
h
h
On connaît la limite de chaque quotient et on a aussi lim v (a + h ) = v (a ), donc
h →0
f (a + h ) − f (a )
lim
= u '(a )v (a ) + u (a )v '(a ).
h
h →0
Donc la fonction f est dérivable en a et f '(a ) = u '(a )v (a ) + u (a )v '(a ).
Cette propriété est vraie pour tout a de l’intervalle I et f = uv , on obtient donc :
(uv )' = u 'v + uv '.
24
© Cned - Académie en ligne
Séquence 4 – MA12
Carré
d’une fonction
On utilise le résultat précédent lorsque les fonctions u et v sont les mêmes, on
2
obtient (u )‘= 2u 'u .
Inverse
On considère une fonction u déﬁnie et dérivable sur un intervalle I et soit a un
nombre de l’intervalle I, on suppose de plus que u (a ) ≠ 0.
1
On appelle f la fonction, déﬁnie en a, égale à l’inverse de u : f = .
u
Pour étudier la dérivabilité de la fonction f en a, on calcule le taux d’accroissement
f (a + h ) − f (a )
et on en cherche la limite éventuelle quand h tend vers 0.
h
1
1
−
On a : f (a + h ) − f (a ) u (a + h ) u (a )
=
h
h
u (a ) − u (a + h )
u (a + h ) × u (a )
=
h
u (a ) − u (a + h ) 1
=
×
u (a + h ) × u (a ) h
u (a ) − u (a + h )
1
=
×
.
h
u (a + h ) × u (a )
u (a + h ) − u (a )
u (a ) − u (a + h )
= u '(a ), on a lim
= −u '(a ) ; et,
h
h
h →0
h →0
2
pour le deuxième quotient, on a lim u (a + h ) × u (a ) = (u (a )) . On obtient donc
Comme
lim
f (a + h ) − f (a ) −u '(a )
lim
.
=
2
h
h →0
(u (a ))
h →0
Donc la fonction f est dérivable en a et f '(a ) =
−u '(a )
(u (a ))
2
.
Cette propriété est vraie pour tout a de l’intervalle I où u est dérivable et à valeurs
‘
 1  −u '
1
non nulles, or f = , on obtient donc :   =
.
u
u
u2
Quotient
On considère deux fonctions u et v déﬁnies et dérivables sur un intervalle I, la
fonction v ne s’annulant pas.
On appelle f la fonction, déﬁnie sur I, égale au quotient des deux fonctions u et
u
v:f = .
v
Pour étudier la fonction dérivée de la fonction f, on utilise les résultats précédents.
1
En effet, la fonction f peut s’écrire sous la forme d’un produit : f = u × .
v
Séquence 4 – MA12
25
© Cned - Académie en ligne
'
1  1
Comme on sait maintenant dériver un produit, on obtient f ' = u '× + u   .
v
v 
1
-v'
On sait aussi dériver une fonction inverse donc : f ' = u '× + u × .
v
v2
u 'v − uv '
.
Et ﬁnalement : f ' =
v2
Exemple 11
Voici six fonctions pour commencer à utiliser ces formules.
Pour chaque fonction suivante, donner l’ensemble de déﬁnition de la fonction
dérivée et son expression.
La fonction f est déﬁnie sur par f ( x ) = −5x 8 .
La fonction g est déﬁnie sur par g ( x ) = −5x 8 + 3x 2 − 2.
La fonction h est déﬁnie sur par h ( x ) =
1
.
x2 + x +1
La fonction k est déﬁnie sur l’intervalle I =  2 ; + ∞  par k ( x ) =
2x + 1
.
3x − 6
La fonction m est déﬁnie sur 0 ; + ∞  par m (x ) = ( 2x + 1) x .
La fonction p est déﬁnie sur par p (x ) = (3x + 1)4 .
Solution
On considère la fonction f déﬁnie sur par f (x ) = −5x 8 . On peut écrire la
fonction f sous la forme f = ku , k étant égal à −5 et u étant la fonction puissance
8, dérivable sur telle que u '(x ) = 8x 7 . La fonction f est donc dérivable sur )
et (ku ' = ku ', donc f '(x ) = − 5 × 8x 7 , f '(x ) = −40x 7 .
Soit g la fonction déﬁnie sur par g ( x ) = −5x 8 + 3x 2 − 2. Cette fonction
g est la somme de trois fonctions dérivables sur : la fonction f, la fonction
déﬁnie par x → 3x 2 qui a pour fonction dérivée x → 3 × 2x et une fonction
constante dont la dérivée est nulle. La fonction g est donc dérivable sur et on
obtient g '( x ) en faisant la somme des dérivées g '( x ) = −40 x 7 + 3 × 2x + 0, soit
g '( x ) = −40 x 7 + 6 x .
Soit h la fonction déﬁnie sur par h ( x ) =
1
(on peut déﬁnir la
x + x +1
fonction h sur car le polynôme x 2 + x + 1 ne s’annule jamais, son discriminant
2
valant −3).
1
On peut écrire la fonction h sous la forme h = , la fonction u étant déﬁnie
u
sur par u ( x ) = x 2 + x + 1. Comme la fonction g précédente, la fonction u est
26
© Cned - Académie en ligne
Séquence 4 – MA12
dérivable sur et u '( x ) = 2x + 1. La fonction h, qui est l’inverse de la fonction
u, est dérivable lorsque la fonction u ne s’annule pas et est dérivable, donc la
−u '( x )
−(2x + 1)
fonction h est dérivable sur et h '( x ) =
, soit h '( x ) =
.
2
2
2
u ( x )
x + x +1
)
(
Soit k la fonction déﬁnie sur l’intervalle I =  2 ; + ∞  par k ( x ) =
2x + 1
.
3x − 6
u
On peut écrire la fonction k sous la forme k = , u et v étant les fonctions afﬁnes
v
déﬁnies sur l’intervalle I par u ( x ) = 2x + 1et v ( x ) = 3x − 6. Ces fonctions u et v
sont dérivables sur leur intervalle de déﬁnition et on a : u '( x ) = 2 et v '( x ) = 3.
La fonction v ne s’annule pas sur I.
u 'v − uv '
,
La fonction k est donc dérivable sur l’intervalle I et k ' =
2
v
u '( x )v ( x ) − u ( x )v '( x )
, c’est-à-dire
donc, pour tout x de I, on a : k '( x ) =
2
v ( x )
k '( x ) =
2( 3x − 6 ) − 3(2x + 1)
2
( 3x − 6 )
, donc k '( x ) =
−15
( 3x − 6 )2
.
Soit m la fonction déﬁnie sur  0 ; + ∞  par m( x ) = ( 2x + 1) x .
On peut écrire la fonction m sous la forme m = uv , où u est la fonction afﬁne
déﬁnie sur 0 ; + ∞ par u ( x ) = 2x + 1et v est la fonction racine carrée.
La fonction u est dérivable partout et u '( x ) = 2, la fonction racine carrée n’est
1
.
dérivable que sur 0 ; + ∞  et sa dérivée est telle que v '( x ) =
2 x
)
Donc la fonction produit m est dérivable sur 0 ; + ∞ et m ' = (uv ' = u 'v + uv '.
Pour tout réel x de 0 ; + ∞  , on a m '( x ) = u '( x )v ( x ) + u ( x )v '( x ),
2x + 1
m '( x ) = 2 x +
.
2 x
soit
Soit p la fonction déﬁnie sur par p ( x ) = ( 3x + 1)4 .
On peut écrire la fonction p sous la forme p = u 2 , où u est la fonction déﬁnie sur
)2
par u ( x ) = ( 3x + 1 .
La fonction u est dérivable sur comme carré d’une fonction et on a
u '( x ) = 2 × 3 × ( 3x + 1 .
)
Donc la fonction p est dérivable sur et p '( x ) = 2 × 6( 3x + 1) × ( 3x + 1)2 , soit
p '( x ) = 12( 3x + 1)3 .
Séquence 4 – MA12
27
© Cned - Académie en ligne
Remarque
On a très peu transformé les expressions qui ont été obtenues par les formules
des dérivées.
En effet, il n’y a pas de raison de transformer une expression lorsqu’on ne sait
pas à quoi elle va servir (ici il s’agit simplement de s’entraîner à appliquer les
formules des opérations sur les dérivées).
2. Polynômes et fonctions rationnelles
Les fonctions polynômes sont construites par additions et multiplications à partir
des fonctions puissances et des constantes.
Les fonctions rationnelles sont les fonctions obtenues en faisant des quotients de
fonctions polynômes.
Tous les résultats résumés dans le tableau précédent prouvent la propriété 4.
Propriété 4
Toute fonction polynôme est dérivable sur .
Toute fonction rationnelle est dérivable sur son ensemble de déﬁnition.
Exemple 13
Les fonctions f , g et p de l’exemple 11 sont des fonctions polynômes, elles sont
dérivables sur .
Les fonctions h et k sont des fonctions rationnelles, elles sont dérivables chacune
sur son ensemble de déﬁnition.
Remarque
C
Remarque 1
Les résultats sur les opérations permettent de calculer les fonctions dérivées de
toutes les fonctions polynômes et de toutes les fonctions rationnelles.
Exercices d’apprentissage
Il s’agit ici d’exercices d’apprentissage des formules de dérivation.
Il est inutile pour l’instant de transformer l’expression obtenue pour une fonction
dérivée.
Des transformations seront souvent nécessaires quand on utilisera la fonction
dérivée et ces transformations dépendront du but recherché (pour l’étude d’un
signe par exemple, factoriser est souvent plus efﬁcace que développer).
Remarque 2
28
© Cned - Académie en ligne
Des calculatrices et des logiciels peuvent calculer des nombres dérivés et
certain(e)s donnent même l’expression des fonctions dérivées. Il est cependant
indispensable de savoir faire ces calculs en utilisant les fonctions de référence et
les théorèmes sur les opérations.
Séquence 4 – MA12
Exercice 12
Dans chaque cas, on donne une fonction f déﬁnie sur un intervalle I.
Dans chaque cas, dire si la fonction f est dérivable sur I et donner l’expression
de f '( x ).
f (x ) =

 7
2
, I =  − ; + ∞ 
3x + 7

 3
f ( x ) = −3x 5 + 4 x 4 − 7x 2 + 3, I = .
f ( x ) = x 3 + 3x 2 −
4
, I = 0 ; + ∞  .
x
f ( x ) = 3 x + 2x , I =  0 ; + ∞  .
f ( x ) = x x + 2x , I =  0 ; + ∞  .
f (x ) =
f (x ) =
Exercice 13
x3 −1
x2 +1
, I = .
x 5
− , I = 0 ; + ∞  .
5 x
Mêmes questions qu’à l’exercice 12.
f (x ) =

1
−3
, I =  ; + ∞  .
2x − 1

2
f (x ) =
1
+ x − 2, I = 0 ; + ∞  .
x
f (x ) =
1
− 3 , I = 0 ; + ∞  .
2x
f (x ) =
2x − 1
, I =  −3 ; + ∞  .
x +3
f ( x ) = ( 3x − 1)2 , I = .
2
 1
f ( x ) =  1+  , I =  0 ; + ∞  .
 x
Exercice 14
Dans chaque cas, on donne l’expression d’une fonction f et son ensemble de
déﬁnition.
Déterminer une équation de la tangente ∆ à la courbe Cf , représentant la
fonction f, au point d’abscisse a.
f ( x ) = x 2 − 2x sur , a = 1.
Séquence 4 – MA12
29
© Cned - Académie en ligne
f (x ) =
1
sur  −1; + ∞  , a = 0.
x +1
f ( x ) = x 3 sur , a = 5.
f (x ) =
x sur 0 ; +∞  , a = 3.
f ( x ) = ( 3x − 1)2 sur , a = 0.
f (x ) =
30
© Cned - Académie en ligne
Séquence 4 – MA12
x2 + x +1
sur  2 ; + ∞  , a = 4.
x −2
5
Premières applications
de la dérivation
Dans ces premières applications, il va s’agir d’un exemple d’utilisation des
approximations afﬁnes, et d’un exemple d’application en physique.
A
Activités
1. Activité 1
Dans cette activité, on va utiliser une méthode qui permet de trouver des valeurs
approchées pour une fonction f dont on ne connaît pas l’expression, mais pour
laquelle on a seulement une valeur et des informations sur sa fonction dérivée.
Avec un tableur, on va déterminer des valeurs approchées de f ( x ) de proche en
proche en utilisant systématiquement l’approximation f (a + h ) ≈ f (a ) + f '(a ) × h.
On admet l’existence d’une fonction f déﬁnie sur [1 ; 4] telle que f (1) = 0 et
f '( x ) = x .
Entrer la lettre x dans la cellule A1 puis 1, la première valeur de x, dans la
cellule A2.
Faire apparaître, dans les cellules de la colonne A, les valeurs 1 à 4 avec le pas h
tel que h = 0, 5.
Entrer « valeur approchée de f (x) » dans la cellule B1, puis 0, c’est-à-dire f (1)
dans la cellule B2.
La formule d’approximation afﬁne donne ici : f (1+ 0, 5) ≈ f (1) + f '(1) × 0, 5 ou
f (1+ 0, 5) ≈ f (1) + 0, 5 × 1.
Dans la cellule B3, où on veut obtenir une valeur approchée de f (1,5), on rentre
donc B2+0,5*RACINE(A2).
Compléter la colonne B en recopiant la formule de la cellule B3 pour avoir les
autres valeurs approchées.
Le diagramme suivant a été fait avec le tableur OpenOfﬁce.
Pour cela, après avoir sélectionné la plage des huit cellules qui apparaissent ici,
on a choisi Diagramme, puis successivement : Le type de diagramme : Ligne,
puis le deuxième choix qui s’appelle Points et Lignes, puis après « suivant » on
a coché : Première colonne comme étiquette et enﬁn on a cliqué sur Terminer.
On obtient ainsi des points ayant pour abscisses (étiquette) les nombres de la
première colonne, la colonne A, et pour ordonnées les valeurs correspondantes
de la colonne B. Le choix Points et Lignes permet de voir les points obtenus et les
segments de droites qui les joignent.
Séquence 4 – MA12
31
© Cned - Académie en ligne
Faire le diagramme complet en sélectionnant la plage des cellules à
partir de A2 jusqu’à la dernière cellule remplie de la colonne B et faire
un diagramme analogue au diagramme ci-contre, en choisissant
Lignes au lieu de Points et Lignes
pour une meilleure lisibilité.
On admet que la fonction f est la fonction déﬁnie sur [0 ; 4] par
2
f ( x ) = ( x x − 1) (on peut vériﬁer la valeur de f (1) et l’expression de f '( x )).
3
2
Sur la feuille de calcul, écrire « valeur de ( x x − 1) » dans la cellule C1, dans
3
C2 calculer la valeur donnée par cette formule pour x = 1(1 est dans la cellule
A2), puis compléter la colonne C en recopiant.
Faire un diagramme analogue au précédent en sélectionnant toutes les
cellules remplies des colonnes A, B et C. Deux courbes doivent s’afﬁcher : la
courbe obtenue en joignant les points correspondants aux valeurs approchées et
2
la courbe obtenue avec les valeurs données par la formule f ( x ) = ( x x − 1).
3
Qu’observe-ton ?
2. Activité 2
Cette activité montre comment la dérivation peut intervenir en sciences physiques.
Une pie (oiseau réputé pour être voleur) est perchée sur un pont et laisse tomber
bêtement un objet qu’elle vient de dérober.
La chute de l’objet est verticale. La courbe (C) ci-dessous représente, en fonction
du temps t (en secondes) écoulé depuis le début de la chute, la distance d (t ) (en
mètres) parcourue par l’objet.
L’objet est lâché à l’instant t = 0 et la courbe correspond au déroulement de la
chute jusqu’au moment où l’objet atteint la rivière.
d(t)
100 m
20 m
O
32
© Cned - Académie en ligne
0,5 s
Séquence 4 – MA12
1s
2s
3s
4s
5 s (t)
Quelle est la durée de la chute ?
De quelle hauteur par rapport à la rivière l’oiseau a-t-il lâché l’objet ?
À quelle vitesse moyenne l’objet tombe-t-il ?
La courbe (C) est en fait la représentation graphique de la fonction d déﬁnie
par d (t ) = 4 , 9t 2 sur [0 ; 5].
Quelle est la vitesse moyenne de l’objet entre les instants t = 2 et t = 2,1 ? entre
t = 2 et t = 2, 01 ? entre t = 2 et t = 2, 001 ?
Comment peut-on déﬁnir la vitesse instantanée de l’objet à l’instant t = 2 ?
Quelle est la vitesse instantanée de l’objet quand il atteint la rivière ?
B
Cours
1. Approximations affines : méthode d’Euler
La méthode qui a été utilisée dans l’activité 1, s’appelle la méthode d’Euler
(mathématicien suisse 1707-1783).
On applique cette méthode pour déterminer des valeurs approchées d’une
fonction f pour laquelle on connaît seulement l’image d’un nombre et l’expression
de la fonction dérivée en fonction de la variable.
Graphiquement, cela correspond à remplacer la courbe représentative de la
fonction f par des segments de droites (tangentes ou parallèles à des tangentes)
et pour les calculs à utiliser l’approximation f (a + h ) ≈ f (a ) + f '(a ) × h.
On a repris l’exemple de l’activité 1 pour illustrer cette méthode, le repère n’est
pas orthonormé pour mieux voir et comprendre les approximations.
Première étape
On calcule l’ordonnée du point de la tangente en A qui a pour abscisse a + h.
f(1)=0
O
y= f(x)
B
f(1,5)
y1= f(1)+f’(1) 0,5
M1
On appelle ce point M1, son ordonnée
y 1 est donc une valeur approchée
de f (a + h ). Le point M1 est un point
approché du point B de la courbe,
d’abscisse a + h.
A
a=1
a+h=1,5
2
tangente en A
Séquence 4 – MA12
33
© Cned - Académie en ligne
Deuxième étape
À partir du point M1 on trace une
droite parallèle à la tangente en B
(B est le vrai point de la courbe, on
ne le connaît pas mais on connaît le
cœfﬁcient directeur de la tangente
en B, c’est f '(1, 5), soit f '(a + h )) .
Pour notre exemple, cette droite
passe par le point M1 (d’abscisse 1,5) et son cœfﬁcient directeur est f '(1, 5), donc le point M2
d’abscisse 2 a pour ordonnée y 2
avec y 2 = y 1 + f '(1, 5) × (2 − 1, 5),
d’où y 2 = y 1 + f '(1, 5) × 0, 5.
y= f(x)
C
f(2)
y2= y1+f’(1,5)x0,5
M2
1
Droite (M1M2)
cœfficient directeur égal à celui
de la tangente en B : f’(1,5)
f’(1,5)x0,5
B
f(1,5)
y1= f(1)+f’(1)x0,5
M1
f’(1)x0,5
f(1)=0
O
A
a=1
a+h=1,5
a+2h=2
tangente en A
cœfficient directeur : f’(1)
Le nombre y 2 est une valeur approchée de f (2), soit f (a + 2h ).
On continue de la même façon (c’est pourquoi on a utilisé la fonctionnalité de
recopie dans le tableur).
La ligne polygonale AM1M2M3… est une courbe approchée de la courbe
représentative de f.
La ﬁgure suivante est la même que la précédente, mais les légendes concernent
uniquement le cas général.
y= f(x)
C
f(a+2h)
y2= y1+f’(a+h)xh
M2
1
Droite (M1M2)
cœfficient directeur égal à celui
de la tangente en B : f’(a+h)
f’(a+h)xh
B
f(a+h)
y1= f(a)+f’(a)xh
h
M1
f ’(a)xh
f(1)=0
O
A
a
a+h
a+2h
tangente en A
cœfficient directeur : f’(a)
Commentaire
34
© Cned - Académie en ligne
Cette méthode sera revue plus loin dans le cours, une autre notion en permettant
alors une présentation plus complète. Vous pourrez donc l’assimiler petit à petit.
Séquence 4 – MA12
2. Vitesse instantanée
Si d (t ) est la distance parcourue par un mobile de l’instant 0 à l’instant t,
alors la vitesse moyenne de celui-ci, entre les instants t et t + h , est égale à :
vmoyenne =
distance parcourue d (t + h ) − d (t )
=
.
durée du parcours
h
On a retrouvé le taux d’accroissement de la fonction d entre t et t + h , ce qui
permet de passer à la déﬁnition suivante.
Définition 6
Si d (t ) est la distance parcourue par un mobile de l’instant 0 à l’instant t,
alors la vitesse instantanée de celui-ci à l’instant t est le nombre v (t )
d (t + h ) − d (t )
, soit v (t ) = d '(t ).
h
h →0
déﬁni par : v (t ) = lim
Généralisation
Tout phénomène physique où une grandeur varie en fonction du temps peut
amener à considérer des vitesses moyennes, des vitesses instantanées et donc à
introduire des fonctions dérivées.
On peut généraliser encore à des phénomènes physiques où une grandeur dépend
d’une autre (qui n’est plus le temps). Là encore on peut étudier les variations
moyennes d’une grandeur en fonction des variations de l’autre, et on aboutit à
des « variations instantanées » qui sont des dérivées.
C
Exercice 15
Exercices d’apprentissage
On admet qu’il existe une fonction f déﬁnie et dérivable sur 0 ; + ∞ telle que
1
f (1) = 0 et f '( x ) = pour tout réel x strictement positif.
x
Sur un tableur, appliquer la méthode d’Euler en utilisant le pas h tel que
h = 0,1 et donner une valeur approchée de f (2).
Modiﬁer la feuille de calcul pour pouvoir choisir la valeur de h.
Donner de nouveau une valeur approchée de f ( 2), en utilisant h = 0, 01 puis
h = 0, 001.
Exercice 16
Une voiture se déplace sur une route. Elle démarre à l’instant t = 0 et la distance
d (t ) (en km) parcourue par le véhicule à l’instant t (en heure) est telle que
d (t ) = −120t 3 + 180t 2 avec t ∈0 ; 1 .
Séquence 4 – MA12
35
© Cned - Académie en ligne
Déterminer la distance parcourue au bout d’une heure, d’une demi-heure, de
10 minutes.
Exprimer, en fonction de t, la vitesse instantanée v (t ) du véhicule à l’instant t.
Déterminer la vitesse instantanée du véhicule à l’instant du départ, au bout de
1 heure, 30 minutes, 10 minutes ?
Quelle est la vitesse maximum atteinte par le véhicule ?
36
© Cned - Académie en ligne
Séquence 4 – MA12
6
Synthèse de la partie 1
de la séquence
Définitions et propriétés
fondamentales
A
Définition 1
Soit f une fonction déﬁnie sur un intervalle I, a et a + h (h ≠ 0 ) deux éléments de l’intervalle I.
Le quotient
f (a + h ) − f (a )
est appelé taux d’accroissement de la fonction f entre a et a + h.
h
Définition 2
Soit f une fonction déﬁnie sur un intervalle I et soit a un nombre réel appartenant à l’intervalle I.
f (a + h ) − f (a )
tend vers un nombre réel quand h tend vers 0 on dit
h
que la fonction f est dérivable en a.
Si le taux d’accroissement
Le nombre réel qui est la limite du taux d’accroissement quand h tend vers 0 est appelé le
f (a + h ) − f (a )
nombre dérivé de la fonction f en a, on le note f '(a ) : lim
= f '(a ).
h
h →0
Définition 3
Soit f une fonction déﬁnie sur un intervalle I et dérivable en a, a étant un nombre réel appartenant
à l’intervalle I.
La tangente à la courbe représentative de f au point d’abscisse a est la droite passant par le
point de la courbe de coordonnées (a ; f (a )) et ayant pour cœfﬁcient directeur f '(a ), le nombre
dérivé en a.
Propriété 1
A
j
0
i
a
Soit f une fonction déﬁnie sur un intervalle I et dérivable en a, a
étant un nombre réel appartenant à l’intervalle I.
La tangente à la courbe représentative de f au point d’abscisse a
est la droite qui a pour équation y = f '(a )( x − a ) + f (a ).
Séquence 4 – MA12
37
© Cned - Académie en ligne
Définition 4
Soit f une fonction déﬁnie sur un intervalle I et soit a un nombre réel
appartenant à l’intervalle I.
Si la fonction f est dérivable en a, on dit que la fonction afﬁne
x → f '(a )( x − a ) + f (a ) est l’approximation afﬁne de f en a.
Remarque
B
On a ainsi un moyen pour calculer des valeurs approchées de certaines images :
f ( x ) ≈ f '(a )( x − a ) + f (a ) ou, en posant x = a + h , f (a + h ) f (a ) + f '(a ) × h.
Fonction dérivée, exemples
des fonctions de référence
Définition 5
On dit qu’une fonction f est dérivable sur un intervalle I si f est déﬁnie sur I
et dérivable en tout point de l’intervalle I.
La fonction, déﬁnie sur l’intervalle I et à valeurs dans , qui à tout réel
x de l’intervalle I associe le nombre dérivé de f en x est appelée fonction
dérivée de f ; cette fonction dérivée est notée f '.
Propriété 2 : Résultats à connaître parfaitement
Fonctions
Les fonctions constantes
f :→
x →k
Les fonctions constantes sont déﬁnies et f ': → dérivables sur .
x →0
Les fonctions afﬁnes
f :→
x → mx + p
Les fonctions afﬁnes sont déﬁnies et f ': → dérivables sur .
x →m
La fonction carré
La fonction carré est déﬁnie et dérivable f ': → sur .
x → 2x
f :→
x → x2
38
© Cned - Académie en ligne
Fonctions dérivées
Séquence 4 – MA12
Propriété 2 : Résultats à connaître parfaitement (suite)
Fonctions
Fonctions dérivées
Les fonctions puissances : Les fonctions puissances sont déﬁnies et f ': → soit n un entier naturel dérivables sur .
x → nx n −1
non nul
f :→
x → xn
La fonction inverse est déﬁnie et dérivable
f ': ∗ → sur  −∞ ; 0  ∪ 0 ; + ∞  .
−1
x→
x2
La fonction inverse
f : * → x→
1
x
La fonction racine carrée
f : 0 ; + ∞  → x→ x
C
La fonction racine carrée est déﬁnie sur f ': 0 ; + ∞  → 

0 ; + ∞ et dérivable seulement sur
1
x→
0 ; + ∞  .
2 x
Attention : la fonction racine carrée est
déﬁnie en 0 mais n’est pas dérivable en 0.
Dérivation : opérations sur les
fonctions
Propriété 3 : Résultats à connaître parfaitement
Ces résultats sont établis, bien sûr, là où les fonctions u et v sont déﬁnies et dérivables, et là où
le dénominateur ne s’annule pas pour les deux derniers cas.
Fonction
Fonction dérivée
u +v
(u + v )' = u '+ v '
ku , k constante réelle
(ku )' = ku '
uv
(uv )' = u 'v + uv '
u2
(u 2 )' = 2u 'u
1
u
 1  −u '
 u  = 2
u
u
v
 u  u 'v − uv '
 v  =
v2
'
'
Séquence 4 – MA12
39
© Cned - Académie en ligne
Propriété 4
Toute fonction polynôme est dérivable sur .
Toute fonction rationnelle est dérivable sur son ensemble de déﬁnition.
D
Premières applications
de la dérivation
Approximations
affines : méthode d’Euler
On applique cette méthode pour déterminer des valeurs approchées d’une fonction
f pour laquelle on connaît seulement l’image d’un nombre et l’expression de la
fonction dérivée en fonction de la variable.
Graphiquement, cela correspond à remplacer la courbe représentative de la
fonction f par des segments de droites (parallèles à des tangentes) et pour les
calculs à utiliser l’approximation f (a + h ) ≈ f (a ) + f '(a ) × h.
Vitesse
instantanée
Définition 6
Si d (t ) est la distance parcourue par un mobile à l’instant t, alors la
vitesse instantanée de celui-ci à l’instant t est le nombre v (t ) déﬁni par :
d (t + h ) − d (t )
v (t ) = lim
, soit v (t ) = d '(t ).
h
h →0
40
© Cned - Académie en ligne
Séquence 4 – MA12
7
Exercice I
Première étape
Exercices
d’approfondissement
On considère la fonction f, déﬁnie sur l’intervalle  −16 ; 16  de la façon suivante :
f (0 ) = 0 et sa représentation graphique, symétrique par rapport à l’axe (Oy), est
expliquée ci-dessous.
Voici la représentation graphique sur l’intervalle [8 ; 16].
y
y=x
j
0
Deuxième étape
8
i
12
16
x
On a construit de façon semblable la courbe représentative sur l’intervalle [4 ; 8]
(dont l’amplitude est égale à la moitié de l’amplitude de l’intervalle [8 ; 16]) et on
a complété par symétrie par rapport à (Oy).
y
y=–x
y=x
j
-6
-4
0
i
4
6
8
12
16
x
Séquence 4 – MA12
41
© Cned - Académie en ligne
Construire, de façon semblable, la courbe sur les intervalles [2 ; 4] et [–4 ; –2].
On continue ainsi et la fonction est déﬁnie sur  −16 ; 16  . Que se passe-t-il
pour la courbe si on fait des zooms-agrandissements centrés à l’origine ? Que
peut-on alors conjecturer ?
Exercice II
Dans cet exercice, il s’agit de faire des pliages !
Sur une feuille de papier, dessiner un segment d’une droite
(D) et placer un point F, comme dans la ﬁgure ci-contre.
Choisir un point H sur la droite (D).
F
(D)
H
Plier la feuille en superposant le point F et le point H et bien
marquer la droite du pliage.
Recommencer avec d’autres points H sur la droite (D).
Qu’observe-t-on ?
Si vous faites cette activité avec un logiciel de géométrie dynamique, que se
passe-t-il quand on éloigne le point F de la droite (D) ?
Exercice III
Soit f la fonction déﬁnie sur  −1; 1 par f ( x ) = 1− x 2 , et soit Cf sa courbe
représentative dans un repère orthonormé.
En utilisant la déﬁnition, montrer que la fonction f est dérivable en a = 0, 5.
Quelle est la valeur de f '(0, 5) ?
Soit A le point de la courbe C d’abscisse 0,5. Ecrire l’équation de la tangente
f
(T) à la courbe Cf au point M.
Cette question est un peu différente des autres dans sa forme. On dit qu’elle
est « avec prise d’initiative », c’est-à-dire que la démarche de résolution ne
vous est pas donnée et que vous devez avoir l’initiative des différentes étapes.
Montrer que la courbe Cf est un demi-cercle. Or, pour un cercle, on a déjà employé
le mot tangente dans les classes de collège.
Montrer que la droite (T) est tangente au demi-cercle au point M, le mot
« tangente » étant utilisé ici avec la signiﬁcation qu’il a en collège.
Exercice IV
On cherche à construire un toboggan.
Son « proﬁl » en coupe doit être une courbe déﬁnie sur un intervalle a ; b  ,
la tangente au point d’abscisse a et la tangente au point d’abscisse b étant
horizontales.
On va former le toboggan en « collant » des parties de deux courbes.
On modélise cette situation de la façon suivante.
On considère une fonction f déﬁnie sur 0 ; 10  par f ( x ) = kx 3 , k étant un
nombre réel constant.
On considère aussi une fonction g du second degré, déﬁnie sur 0 ; 10  et dont
le sommet est le point de coordonnées (10 ; 8).
42
© Cned - Académie en ligne
Séquence 4 – MA12
Écrire l’expression de g ( x ) dans laquelle un des cœfﬁcients reste indéterminé
pour l’instant (on choisira la forme la plus adapté : voir la partie 1 de la séquence
3).
On pourra « recoller » les courbes si elles ont un point commun et la même
tangente en ce point.
On souhaite que ce point commun ait pour abscisse 5.
Écrire le système de deux équations à deux inconnues traduisant ces conditions
(les inconnues sont k et le cœfﬁcient encore indéterminé de la fonction g).
Résoudre le système.
Faire une ﬁgure en traçant seulement la courbe de la fonction f sur  0 ; 5  et
la courbe de g sur 5 ; 10  .
Séquence 4 – MA12
43
© Cned - Académie en ligne
e
2
partie
Trigonométrie
Sommaire
1. Pré-requis
2. Trigonométrie
3. Synthèse de la partie 2 de la séquence
4. Exercices d’approfondissement
44
© Cned - Académie en ligne
Séquence 4 – MA12
1
2 Pré-requis
A
Trigonométrie dans un triangle
rectangle
1. Sinus et cosinus d’un angle dans un
triangle rectangle
C
On considère un triangle ABC rectangle en A et on s’intéresse
à l’un des angles en B ou en C.
et ACB
Remarquons tout d’abord que ces deux angles ABC
sont nécessairement aigus (et non nuls).
Vous avez vu en collège les déﬁnitions suivantes.
B
A
Définition
est aigu et, on déﬁnit le
Dans le triangle ABC rectangle en A, l’angle ABC
= AC , et le cosinus de cet angle par :
sinus de cet angle par : sin ABC
BC
AB
cos ABC = .
BC
( )
( )
Remarques
( )
C’
B
( )
et cos ABC
ne dépendent que de l’angle ABC
a) Ces deux nombres, sin ABC
et non pas du triangle dans lequel on observe cet angle.
C
et A'BC'
qui sont
Dans la ﬁgure ci-contre, les angles ABC
A’
égaux ont même sinus et même cosinus (conséquence du
théorème de Thalès).
et cos ABC
b) Chacun de ces deux nombres, sin ABC
caractérise l’angle ABC.
A
Autrement dit si l’on connaît
connaît l’angle ABC.
( ) ( )
ou cos ABC
sin( ABC
) ( ) on
Vous avez déjà utilisé cette caractéristique en collège ou en seconde lorsque vous
avez cherché, à la calculatrice, une valeur approchée d’un angle dont vous aviez
calculé le sinus ou le cosinus.
Séquence 4 – MA12
45
© Cned - Académie en ligne
왘
Exemple
( )
= 0, 9. A la calculatrice, vous allez calculer une
Vous avez calculé que cos ABC
en utilisant la fonction « réciproque » de la fonction
valeur approchée de ABC
cosinus, notée cos−1 sur les TI et Acs sur les Casio, en ayant pris soin de vériﬁer
que la calculatrice est bien réglée en degrés.
)
vaut environ 25,842°.
On obtient : cos−1( 0, 9 ≈ 25, 842. Donc l’angle ABC
( )
( )
2
2
on a toujours : sin ABC
 + cos ABC
 = 1.
c) Quel que soit l’angle ABC

 

En effet, le triangle ABC étant rectangle en A on a : AB2 + AC2 = BC2 (théorème
de Pythagore).
2
2
 AB   AC 
AB2 AC2
+
= 1, que l’on peut écrire   +   = 1.
Ce qui nous donne :
 BC   BC 
BC2 BC2
2
2
 + sin ABC
 = 1.
On retrouve bien : cos ABC

 

( )
( )
2. Tangente d’un angle dans un triangle rectangle
Dans les mêmes conditions que ci-dessus, on a aussi.
Définition
est aigu et, on déﬁnit la
Dans le triangle ABC rectangle en A, l’angle ABC
= AC .
tangente de cet angle par : tan ABC
AB
( )
Remarques
B
( )
que les remarques a)
a) et b) On a les mêmes remarques à propos de tan ABC
et cos ABC
.
et b) à propos de sin ABC
( ) ( )
sin( ABC
)
=
.
c) On a : tan( ABC
) cos( ABC
)
Cercle trigonométrique
1. Cercle trigonométrique
Ꮿ
Définition
Le plan est rapporté à un repère orthonormé
(O, I, J .
)
On appelle cercle trigonométrique le cercle Ꮿ de
centre O et de rayon 1, orienté dans le sens inverse
des aiguilles d’une montre.
46
© Cned - Académie en ligne
Séquence 4 – MA12
I’
J
0
J’
+
I
Remarques
a) Le sens inverse des aiguilles d’une montre est appelé sens positif, l’autre,
sens négatif (on dit aussi sens direct et sens indirect).
b) Le cercle trigonométrique étant de rayon 1, il passe par les points I et J.
c) Sur le cercle trigonométrique, le trajet le plus court pour aller de I à J est d’y
aller dans le sens positif. C’est pour cela que l’on dit que le repère (O, I, J est
orthonormé direct.
)
2. Enroulement de la droite numérique sur
le cercle trigonométrique
Etant donné le cercle trigonométrique Ꮿ de centre O, dans
le repère orthonormé direct (O, I, J , on considère la droite
(IK tangente à Ꮿ passant par I, K étant le point de
coordonnées K (1; 1 .
2
Ꮿ
I’
J
+K
)
x
1
)
–1
Voir graphique ci-contre.
)
Ensuite, on « enroule » cette droite réelle (IK sur le cercle
trigonométrique (voir graphiques ci-dessous).
–2
2
J
x
M
Ꮿ
I’
)
La droite (IK représente donc l’ensemble R des nombres
réels.
y
J’
)
Sur cette droite, on considère le repère (I, K , ce qui permet
d’établir une graduation. A chaque point de cette droite
correspond un nombre réel, et à chaque nombre réel
correspond un point de la droite (0 correspond au point I,
1 au point K).
0
I
0
)
0
K
1 +
2
M
Ꮿ
0
I
I’
–1
K
1 +
0
N
y
J’
x
J
0
I
y
–1
J’
–2
Chaque graduation positive de la droite (par exemple x sur les graphiques ci
dessus) correspond à un point M du cercle tel que la longueur de l’arc IM,
parcouru dans le sens positif, soit égale à x.
Séquence 4 – MA12
47
© Cned - Académie en ligne
De même, chaque graduation négative (par exemple y sur les graphiques cidessus) correspond à un point N du cercle tel que la longueur de l’arc IN,
parcouru dans le sens négatif, soit égale à y (valeur absolue).
Bien entendu, lorsque l’on continue à
« enrouler » la droite réelle (IK sur le
cercle trigonométrique, plusieurs
graduations, aussi bien positives que
négatives, correspondent au même
point.
)
N
–2
)
0
I
y
0
I’
Par exemple, sur le graphique cicontre, le point P correspondant à la
graduation 2 correspond aussi à la
graduation ( 2 − 2π .
K
1 +
M
2–2π
Ꮿ
x
J
2 P
–1
J’
En effet, le cercle trigonométrique étant de rayon
1, son périmètre mesure 2π.
Puisque P correspond à la graduation 2, l’arc IP, parcouru dans le sens positif,
a pour longueur 2.
Donc, l’arc IP, parcouru dans le sens négatif, a pour longueur ( 2π − 2 . Le point
P correspond donc à la graduation négative ( 2 − 2π , dont ( 2π − 2 est la valeur
absolue.
)
)
)
Propriété
)
Lorsque l’on « enroule » la droite réelle (IK sur le cercle trigonométrique,
chaque nombre réel correspond à un seul point du cercle.
Par contre chaque point du cercle correspond à une inﬁnité de nombres
réels.
Remarque
Puisqu’il faut faire un tour de cercle complet (dans le sens positif ou dans le sens
négatif) pour retomber sur le même point, et puisque le périmètre du cercle est
2π, un point du cercle (par exemple M sur le graphique ci-dessus) correspondra
à des réels dont la différence est un nombre entier de fois 2π.
Ainsi, si l’on parcourt le cercle dans le sens positif, le point M correspond aux
réels x, ( x + 2π , ( x + 4π , ( x + 6π , … etc.
)
)
)
Si l’on parcourt le cercle dans le sens négatif, le point M correspond aussi aux
réels ( x − 2π , ( x − 4π , ( x − 6π , … etc.
)
)
)
)
)
De la même façon, le point P correspond aux réels 2, ( 2 + 2π , ( 2 + 4 π ,
(2 + 6π , … etc. et (2 − 2π , (2 − 4 π , (2 − 6π , … etc.
)
48
© Cned - Académie en ligne
Séquence 4 – MA12
)
)
)
C
Cosinus et sinus d’un nombre réel
1. Cosinus et sinus d’un nombre réel
Après avoir « enroulé » la droite réelle sur le cercle trigonométrique, on sait que
chaque nombre réel x correspond à un point M du cercle (voir graphique cidessous).
Définition
2
)
On appelle cosinus du nombre x, et on note cos ( x ,
l’abscisse du point M dans le repère (O, I, J .
)
sin(x)
Ꮿ
De même, on appelle sinus du nombre x, et on note
sin( x , l’ordonnée du point M dans le repère (O, I, J .
)
K
Mx +
J
I’
)
0
cos(x)
(Voir graphique ci-contre).
0
I
–1
J’
Remarques
a) Puisqu’une inﬁnité de nombres réels correspondent au même point M, tous
ces nombres ont le même cosinus et le même sinus. On a par exemple :
)
)
)
)
)
sin( x ) = sin( x + 2π ) = sin( x + 18 π ) = sin( x − 2π ) = sin( x − 6 π ).
cos ( x = cos ( x + 2π = cos ( x + 18 π = cos ( x − 2π = cos ( x − 6 π .
2P
sin(2)
Ꮿ
I’
K
J
x +
0
I
cos(2) 0
–1
5π
—
6
π R
I’
2
)
)
)
Et bien sûr, cos ( 2 + 2π < 0, cos ( 2 + 18 π < 0,
)
cos ( 2 − 2π < 0.
)
)
Et bien sûr, sin( 2 + 2π > 0, sin( 2 + 18 π > 0,
)
π
— π
J 2 —
3 π
—
T
Q 4π
—
6
S
0
0
I
J’
)
sin( 2 − 2π > 0.
J’
Ꮿ
b) Comme certains points du cercle ont des abscisses négatives,
ou des ordonnées négatives, certains nombres réels ont des
cosinus ou des sinus négatifs.
Sur le graphique ci-contre, on voit que cos ( 2 < 0
et sin( 2 > 0.
2. Angles particuliers
et réels particuliers
Le cercle trigonométrique étant de rayon 1, son périmètre
mesure 2π. Donc le demi-périmètre, c’est-à-dire la longueur
de l’arc II', mesure π.
Par conséquent le nombre π correspond au point I’ et l’angle
vaut 180° (voir ci-contre).
IOI'
De même, la longueur de l’arc I J (obtenu en se déplaçant
dans le sens positif), le quart du périmètre du cercle, mesure
–1
π
π
. Par conséquent le nombre correspond au point J et
2
2
vaut 90°.
l’angle IOJ
π π
π
On peut faire de même avec les nombres , ou
en divisant le demi3 4
6
Séquence 4 – MA12
49
© Cned - Académie en ligne
périmètre par 3, par 4 ou par 6.
π
vaut 60°.
Le nombre correspond au point T et l’angle IOT
3
π
vaut 45°.
Le nombre correspond au point Q et l’angle IOQ
4
π
vaut 30°.
Le nombre correspond au point S et l’angle IOS
6
En étendant cette idée on peut aussi associer des angles particuliers aux nombres
2π 3π
5π
,
ou
(point R sur le graphique).
3 4
6
Remarque
π
6
Nombre réel x
0
(en degré)
Angle IOM
0°
π
4
30° 45°
π
3
π
2
2π
3
3π
4
5π
6
π
60° 90° 120° 135° 150° 180°
Plus généralement, si M est un point du cercle trigonométrique, la longueur de
est proportionnelle à l’angle IOM.
l’arc IM
Comme π correspond à un angle de 180°, un nombre positif x compris entre 0
°
 180 
et π correspondra à l’angle 
x .
 π 
Réciproquement, un angle de a° compris entre 0° et 180° correspondra au
π
a.
nombre réel
180
3. Cosinus et sinus des nombres compris
entre 0 et π
2
2
J
Mx
sin(x)
Ꮿ
a°
I’
0
H
cos(x)
0
I
–1
J’
© Cned - Académie en ligne
)
)
)
Appelons H le projeté orthogonal de M sur la droite (OI
(voir graphique ci-contre), et notons a la valeur en degré de
l’angle IOM.
Dans le triangle HOM, rectangle en H, on a :
= sin(a ) = HM .
= cos(a ) = OH et sin HOM
cos HOM
OM
OM
Or OM = 1 puisque c’est le rayon du cercle trigonométrique et OH = cos ( x
puisque c’est l’abscisse du point M (abscisse qui est positive). On obtient donc :
= cos(a ) = cos ( x = cos x .
cos HOM
(
1
( )
( )
( )
50
π
Pour un nombre réel x compris entre 0 et
, donc
2
correspondant à un point M situé sur l’arc I J précisé page
précédente, regardons à quoi correspondent cos ( x et
sin( x .
Séquence 4 – MA12
)
)
)
)
De même HM = sin( x puisque c’est l’ordonnée du point M (ordonnée qui est
positive). On obtient donc :
= sin(a ) = sin( x = sin x .
sin HOM
(
1
)
( )
)
Propriété
π
Les cosinus et sinus d’un nombre x compris entre 0 et , sont les
2
correspondant.
cosinus et sinus de l’angle IOM
On a, entre autres, les valeurs suivantes :
Nombre réel x
0
π
6
π
4
π
3
π
2
(en degré)
Angle IOM
0°
30°
45°
60°
90°
cos ( x = cos IOM
)
( )
1
3
2
2
2
1
2
0
)
( )
0
1
2
2
2
3
2
1
sin( x = sin IOM
De plus, pour tout réel x, on a :
cos2(x ) + sin2(x ) = 1
Séquence 4 – MA12
51
© Cned - Académie en ligne
1
2 Trigonométrie
A
Activités
1. De quel côté ?
= BDA
= 30°.
� Construire un triangle équilatéral ABC, et un point D tel que BAD
� Que peut-on dire du triangle ACD ?
2. Bissectrice ?
= 45° et un point D tel que BAD
= 45°.
� Construire un triangle ABC tel que BAC
( )
� Que peut-on dire de la droite AB ? Des points A, C et D ?
B
Cours
1. Cercle trigonométrique et angles orientés.
Radian
On a vu dans l’activité 1 que, pour éviter certaines ambiguïtés dans les repérages
angulaires, il était intéressant, voire indispensable d’orienter les angles.
Pour cela, il est nécessaire, lorsque l’on déﬁnit un angle, de préciser quel est le
premier côté de l’angle, quel est le second côté.
Pour ce faire, à l’aide du cercle trigonométrique,
nous allons déﬁnir des angles
orientés dont le premier côté sera le vecteur OI et le second le vecteur OM, M
étant un point du cercle.
Par exemple, pour les points P et S tels
= IOS
= 30° on déﬁnit les
que IOP
angles orientés OI, OP et OI, OS
(voir graphique ci-contre).
) (
(
52
© Cned - Académie en ligne
Séquence 4 – MA12
)
P
)
Si l’on va, sur le cercle trigonométrique,
de I à P par le plus court chemin,
on voit que l’on tourne dans le sens
direct, en décrivant un angle
de 30° :
on mesurera l’angle OI, OP avec une
valeur positive (30°).
(
J
0
I’
I
S
330°
J’
30°
690°
–30°
Si l’on va, sur le cercle trigonométrique, de I à S par le plus court chemin, on
voit que l’on tourne
dans
le sens indirect, en décrivant un angle de 30° : on
mesurera l’angle OI, OS avec une valeur négative (–30°), ce qui le distingue
du précédent.
)
(
Mais on peut aussi aller de I à S en tournant dansle sens
direct, en décrivant alors
un angle de 330° : on mesurera alors l’angle OI, OS avec une valeur positive
(330°).
(
)
On peut même aller de I à S en tournant dans le sens direct et en décrivant
plus d’un tour complet ; on décrit alors un angle de 690° : on mesurera l’angle
OI, OS avec une valeur positive (690°).
(
)
Et ainsi de suite …
On
va
pouvoir, tout en faisant la distinction entre les angles orientés
voit
que l’on
OI, OP et OI, OS , mesurer chacun d’entre eux avec plusieurs valeurs, positives
et négatives.
(
) (
)
En fait on peut même énoncer la propriété suivante.
Propriété 1
Chaque angle orienté OI, OM a une inﬁnité de mesures positives
(quand on va du premier côté au second en tournant dans le sens direct, et
en faisant un certain nombre de tours complets avant de s’arrêter), et une
inﬁnité de mesures négatives (de la même façon en tournant dans le
sens indirect).
)
(
On retrouve, pour les angles orientés OI, OM , une situation analogue à celle
que l’on a vue pour le point M lorsque l’on « enroule » la droite réelle sur le
cercle trigonométrique : M correspond à une inﬁnité de nombre réels.
)
(
Cette analogie fait que l’on peut considérer que les nombres réels sur le
cercle trigonométrique mesurent directement les angles orientés de la forme
OI, OM : π mesure l’angle plat, OI, OI' , que l’on peut aussi mesurer par 180°,
π
π
mesure l’angle droit direct, OI, OJ , de 90°, − mesure l’angle OI, OS , de
6
2
–30°, etc.
(
)
(
(
)
)
(
)
On a ainsi déﬁni une nouvelle unité de mesure des angles orientés que l’on
appelle le radian.
Définition 1
Le radian est l’unité de mesure des angles orientés telle qu’un angle plat
direct mesure π radians. On le note rad.
π
Par exemple on notera : OI, OJ = 90° = rad.
2
(
)
Séquence 4 – MA12
53
© Cned - Académie en ligne
La proportionnalité entre la mesure en degrés et la mesure en radians, due à
l’enroulement de la droite réelle sur le cercle trigonométrique, fait que l’on a la
propriété suivante.
Propriété 2
π
Comme π rad = 180 , on a l’égalité 1 =
rad, et donc :
180
π
a =
a rad.
180
°
°
 180 
 180 
x .
Réciproquement, 1 rad = 
, et donc : x rad = 
 π 
 π 
J
Comme on l’a vu en déﬁnissant la
façon de mesurer les angles orientés,
chaque angle orienté OI, OM a une
(
M
α
)
inﬁnité de mesures positives, et une
0
I’
inﬁnité de mesures négatives. Cela
reste vrai lorsque l’on mesure les
angles en radians.
I
α+2π
α–2π
J’
Si l’une des mesures en radians de l’angle orienté OI, OM est α, on a une
)
(
inﬁnité d’autres valeurs possibles pour le mesurer : α + 2π , α + 4 π , α + 6 π , …
etc. α − 2π , α − 4 π , α − 6 π , … etc.
Lorsque l’on veut donner la mesure en radians d’un angle orienté, en règle
générale, on donne la mesure (il n’y en a qu’une) appartenant à l’intervalle
 − π ; π  . On dit que c’est la mesure principale de l’angle.
Propriété 3
Un angle orienté de la forme OI, OM a une inﬁnité de mesures en
radians.
Si l’une des mesures en radians de l’angle orienté OI, OM est α, les
autres mesures sont tous les nombres de la forme α + k 2π avec k ∈.
(
Remarques
)
(
)
� Lorsqu’on écrit la mesure en radians d’un angle orienté, on omet souvent
de préciser « k ∈ » ; il est sous entendu, car « évident », que k est un entier
relatif.
� De même, on écrit α + 2k π plutôt que α + k 2π , car cela se prononce plus
facilement : « deux k pi » au lieu de « k fois deux pi ».
� Nous conserverons, la plupart du temps ces notations, mais on trouve aussi
d’autres façons d’écrire.
54
© Cned - Académie en ligne
Séquence 4 – MA12
Au lieu d’écrire
OI, OM = α + 2k π avec k ∈, on écrit souvent
OI, OM = α (2π ) ou OI, OM = α (mod 2π ), que l’on lit « OI, OM = α à un
multiple de 2π près », ou « OI, OM = α à 2π près », ou « OI, OM = α modulo
2π ».
Toutes ces écritures veulent dire la même chose : il y a une inﬁnité de mesures
d’un angle orienté, et elles diffèrent toutes d’un nombre entier de tours.
Ce qui est important c’est de bien se souvenir qu’un angle orienté a une inﬁnité
de mesures en radians.
Il arrive aussi que l’on omette d’écrire +2k π ou (2π) ou (mod 2π). C’est alors
toujours sous-entendu.
(
(
)
(
(
)
)
)
(
Définition 2
(
)
)
Parmi toutes les mesures en radians de l’angle orienté OI, OM , on appelle
)
(
mesure principale de l’angle celle qui appartient à l’intervalle  − π ; π  .
2. Angle orienté de vecteurs non nuls.
Mesure principale
Regardons maintenant comment l’on va étendre cette notion d’angle orienté à
deux vecteurs non nuls quelconques du plan.
Siles deux
vecteurs sont construits à partir du même point, prenons les vecteurs
AB et AC, il est assez simple de voir comment l’on va mesurer l’angle qu’ils font.
On va « superposer » un cercle trigonométrique sur les deux vecteurs, en faisant
coïnciderle centre du cercle et le point commun A, et en faisant en sorte que le
vecteur OI du cercle trigonométrique soit colinéaire et de même sens que le
premier vecteur de l’angle.
Ceci implique,
bien
entendu,
que
l’on
ait
décidé
si
c’est
l’angle
AB, AC ou
l’angle AC, AB que l’on veut étudier. C’est d’ailleurs l’intérêt de la notion
d’angle orienté.
Ensuite
on
détermine le point M du cercle trigonométrique tel que les vecteurs
AC et OM soient colinéaires et de
même
sens (voir ﬁgure
ci-dessous).
On déﬁnit alors l’angle orienté AB, AC par l’égalité AB, AC = OI, OM .
C’est la même procédure que ce que vous avez déjà fait avec un rapporteur, mais
en tenant compte de l’orientation.
)
(
)
(
(
)
C
C
) (
(
M
)
J
α
B
I
B
A0
A
I’
J’
Séquence 4 – MA12
55
© Cned - Académie en ligne
Si les deux
vecteurs
ne sont pas construits à partir du même point, par exemple
vecteurs EF
et GH, ou s’ils sont déﬁnis sans référence à des points, par exemple
vecteurs u et v , on construit d’abord, à partir de la même origine, deux vecteurs
égaux aux précédents, et on procède comme dans le premier cas (voir le graphique
ci-dessous pour mesurer l’angle u , v où AB = u et AC = v ).
( )
C
C
u
M
J
α
v
B
I
B
A0
A
I’
J’
Bien entendu, comme on l’a vu dans le paragraphe précédent, une fois déterminée
une valeur α de l’angle, on a une inﬁnité d’autres valeurs possibles pour le
mesurer : α + 2π , α + 4 π , α + 6 π , … etc. α − 2π , α − 4 π , α − 6 π , … etc.
Définition 3
La donnée de deux
vecteurs
non
nuls
u
et v , dans cet ordre, détermine un
angle orienté u , v .
On déﬁnit les mesures en radians de l’angle orienté u , v en référence au
cercle trigonométrique.
( )
( )
Propriété 4
Un angle orienté u , v a une inﬁnité de mesures en radians.
Si l’une des mesures en radians de l’angle orienté u , v est α, les autres
( )
( )
mesures sont tous les nombres de la forme α + 2k π avec k ∈.
Parmi toutes les mesures en radians de l’angle orienté u , v on appelle
mesure principale de l’angle celle qui appartient à l’intervalle  − π ; π  .
( )
Remarques
� Bien souvent, il arrive que l’on confonde une mesure d’un angle orienté et
l’angle orienté lui-même. Ce n’est en général pas trop gênant.
� Pour mesurer l’angle AB, AC , on admettra que, au lieu de faire pivoter
le cercle trigonométrique
de
façon
que
le
vecteur
OI
soit colinéaire et de
même sens que AB, on peut garder lecercle
trigonométrique dans sa position
« standard », mesurer l’angle orienté OI, AC , mesurer l’angle orienté OI, AB
et le retrancher de l’angle précédent.
(
)
(
56
© Cned - Académie en ligne
Séquence 4 – MA12
)
(
)
C
M
I’
Sur le graphique ci-contre, on a OI, AC = β, OI, AB = γ ,
et AB, AC = β − γ = α.
Ceci« marche » quelle que soit la position des vecteurs AB
et AC. C’est une conséquence directe de l’orientation des
angles, et l’une des raisons pour lesquelles on a introduit
cette notion.
J
α
β
A 0
)
(
B γ I
(
) (
)
Nous admettrons les propriétés suivantes sur les angles
orientés, propriétés faciles à vériﬁer sur des exemples.
J’
Propriété 5
Quels que soient les vecteurs non nuls u , v et w on a :
a. u , u = 0 + 2k π et u , − u = π + 2k π ;
( )
( )
b. (v , u ) = − (u , v ) + 2k π ;
c. (u , v ) + (v , w ) = (u , w ) + 2k π ; c’est ce que l’on appelle la relation de
Chasles pour les angles orientés ;
d. u , − v = −u , v = u , v + π + 2k π.
(
Démonstration
) (
) ( )
a. C’est évident.
b. C’est une conséquence immédiate de la notion d’orientation.
c. On admettra cette propriété (relation de Chasles) très utile pour les calculs
angulaires.
d. Cette propriété se démontre facilement avec les précédentes. En effet on a :
u , − v = u , v + v , − v d’après la relation de Chasles, et donc
u , − v = u , v + π d’après la première propriété.
(
(
) ( )(
) ( )
)
Vous démontrerez vous-même la deuxième égalité.
3. Angle orienté de vecteurs et configurations
de base
Quelques conﬁgurations élémentaires s’expriment facilement à l’aide des angles
orientés de vecteurs.
Séquence 4 – MA12
57
© Cned - Académie en ligne
a. Alignement, parallélisme
Propriété 6
Trois points distincts A, B et C sont alignés si et seulement si :
CA , CB = 0 + 2k π ou CA , CB = π + 2k π.
)
(
C
Remarque
)
(
A
B
On a même une propriété plus précise.
A
C
Les points A et B étant distincts, on a :
C ∈ AB  ⇔ CA, CB = π + 2k π.
(
B
π
)
Propriété 7
Quatre points distincts A, B, C et D étant donnés, les droites (AB) et (CD)
sont parallèles si et seulement si :
AB, CD = 0 + 2k π ou AB, CD = π + 2k π.
)
(
)
(
A
B
D
C
b. Orthogonalité
Propriété 8
Quatre points distincts A,
B, C et D étant donnés, les
droites (AB) et (CD) sont
orthogonales si et seulement si :
π
AB, CD = + 2k π
2 π
ou AB, CD = − + 2k π.
2
(
58
© Cned - Académie en ligne
Séquence 4 – MA12
(
)
)
C
D
A
B
c. Bissectrice
Propriété 9
)
Étant donnés trois points distincts A, B et C, la droite ( AK est bissectrice de
si et seulement si : AB, AK = AK , AC + 2k π.
BAC
) (
(
)
C
K
C
A
K
A
B
B
d. Somme des angles d’un triangle
Propriété 10
Etant donnés trois points distincts A, B et C, on a :
AB, AC + BC, BA + CA , CB = π + 2k π.
)(
(
Démonstrations
)(
)
� Construisons les points D et E tels que BC = AD et BA = AE.
D
On a : BC, BA = AD, AE + 2k π
et CA , CB = CA , DA + 2k π.
C
(
(
) ( )
) ( )
Or, d’après les propriétés vues au
paragraphe précédent, on a :
−u , − v = −u , v + π + 2k π.
E
(
A
) (
)
B
Donc −u , − v = u , v + π + π = u , v + 2k π.
On obtient donc : CA , CB = CA , DA = −CA , − DA = AC , AD + 2k π.
( )
) ( )
( ) ( ) (
(
) (
)
Et par conséquent :
AB, AC + BC, BA + CA , CB = AB , AC + AD, AE + AC, AD + 2k π..
(
)(
)(
) (
)(
)(
)
La relation de Chasles, appliquée deux fois, nous permet de simpliﬁer cette
somme :
AB, AC + BC, BA + CA , CB = AB , AD + AD, AE = AB, AE + 2k π..
(
)(
)(
) (
)(
) (
)
Séquence 4 – MA12
59
© Cned - Académie en ligne
Comme les vecteurs AB et AE sont opposés, on obtient ﬁnalement :
AB, AC + BC, BA + CA , CB = AB , AE = π + 2k π.
)(
(
)(
) (
)
� Proposons une autre démonstration où l’on voit l’efﬁcacité des propriétés de
calcul avec les angles orientés et en particulier de la relation de Chasles.
On a : AB, AC = AB, CA + π + 2k π puisque CA = − AC
et BC, BA = CB, BA + π + 2k π puisque CB = −BC.
(
(
) (
) (
)
)
Donc on a :
AB, AC + BC, BA + CA , CB =  AB , CA + π  +  CB, BA + π 

 

+ CA , CB + 2k π.
)(
(
)(
) (
)
)
)
(
(
Soit :
AB, AC + BC, BA + CA , CB =  AB , CA + CA , CB + CB, BA 


+2π + 2k π.
)(
(
)(
) (
)(
)(
)
En appliquant la relation de Chasles on obtient :
AB, AC + BC, BA + CA , CB = AB , BA + 2π + 2k π.
Soit : AB, AC + BC, BA + CA , CB = 3π + 2k π.
Et donc : AB, AC + BC, BA + CA , CB = π + 2k π. Normalement, on devrait
noter « = π + 2k ' π » car ce n’est pas le même coefﬁcient multiplicateur qu’à la
ligne précédente (on sait même que k ' = k + 1).
(
)(
(
(
)(
)(
)(
)(
) (
)(
)
)
)
En fait, on fait souvent cet « abus de notation », car la signiﬁcation de l’écriture
+2k π est que k prend toutes les valeurs de , or dans ce cas, k’ prend aussi
toutes les valeurs de .
Remarques
1. Pour cette propriété, il est très important de prendre les trois angles du triangle
avec des mesures principales de même signe (toutes les trois positives sur le
dessin de gauche ci-dessous, toutes les trois négatives sur le dessin de droite).
C
C
A
A
B
B
2. Lorsque l’on passe successivement de A à B puis à C en tournant dans le sens
direct sur le cercle circonscrit au triangle, on dit que le triangle ABC est
direct.
60
© Cned - Académie en ligne
Séquence 4 – MA12
e. Angle inscrit, angle au centre
Propriété 11
M
Soit deux points distincts A et B
d’un cercle de centre O.
Pour tout point M du cercle, distinct
de A et B, on a :
OA , OB = 2 × MA , MB + 2k π.
)
(
0
)
(
B
A
Démonstration
Cette démonstration sera faite dans l’exercice 11.
4. Cosinus et sinus d’un angle orienté quelconque
On peut maintenant revenir surlatrigonométrie, et déﬁnir les cosinus et sinus de
n’importe quel angle orienté u , v , en le mesurant en radians.
( )
Définition 4
Le cosinus et le sinus d’un angle orienté u , v dont une mesure en
( )
radians est x, sont le cosinus et le sinus du nombre x, c’est-à-dire l’abscisse
et l’ordonnée du point M du cercle trigonométrique correspondant à x.
La connaissance des cosinus et sinus des angles particuliers compris entre 0
π
radian et
radian (c’est-à-dire entre 0° et 90°), et les symétries présentes dans
2
le cercle trigonométrique, font que l’on connaît les cosinus et sinus d’une inﬁnité
d’angles particuliers.
On a par exemple les valeurs suivantes :
x (mesure en radians
de l’angle)
−
Point du cercle
6
=−
 π
 6 
=
( )
sin 
2π
1
2
3
3
2
 π
 3 
− cos 
 π
 3 
− sin 
π
2π
17 π
4
3
6
F
G
R
−
E
 π
 6 
− cos 
sin x
−
R
( )
cos x
7π
=−
=−
1
2
3
2
 π
 4 
=
 π
 4 
=−
cos 
− sin 
 π
 3 
2
− cos 
2
2
2
 π
 3 
sin 
=
=−
1
2
3
2
 π
− cos  
 6
 π
 6 
sin 
=−
=
3
2
1
2
Séquence 4 – MA12
61
© Cned - Académie en ligne
En effet, on peut voir sur le graphique ci-dessous que :
2π
—
3
G
17π
—& —
– 7π
6 6
π R
I’
—E
– 2π
3
π
—
J 2
0
π
—
π
T3 —
Q4
π
S—
6
0
I
π
—
–
F 4
J’
)
tMFQPJOU3FTUMFTZNÏUSJRVFEF4QBSrapport à la droite (OJ ; ils ont donc des
abscisses opposées et des ordonnées égales ;
tMF QPJOU & FTU MF TZNÏUSJRVF EF5 QBS SBQQPSU BV QPJOU 0 JMT POU EPOD EFT
abscisses opposées et des ordonnées opposées ;
)
tMFQPJOU'FTUMFTZNÏUSJRVFEF2QBSSBQQPSUËMBESPJUF (OI ; ils ont donc des
abscisses égales et des ordonnées opposées ;
)
tMFQPJOU(FTUMFTZNÏUSJRVFEF5QBSSBQQPSUËMBESPJUF (OJ ; ils ont donc des
abscisses opposées et des ordonnées égales.
De façon plus générale on a les résultats suivants.
Propriété 12
Pour tout réel quelconque x :
Mesure en radians
de l’angle
−x
π−x
cos ( − x = cos ( x
)
)
sin( − x ) = − sin( x )
cos ( π − x = − cos ( x
Mesure en radians
de l’angle
x +π
π
−x
2
Cosinus
cos ( x + π = − cos ( x
Sinus
sin( x + π = − sin( x
Cosinus
Sinus
62
© Cned - Académie en ligne
Séquence 4 – MA12
)
)
sin( π − x ) = sin( x )
)
)
π

cos  − x  = sin( x
2

)
)
)
π

sin  − x  = cos ( x
2

)
J
Q
π
I’
R
S
En effet, on peut voir sur le graphique cicontre que :
d
π
2 x
π–x
tMFQPJOU1FTUMFTZNÏUSJRVFEF.QBSSBQQPSU
à la droite (OI ; ils ont donc des abscisses
égales et des ordonnées opposées ;
)
M
x 0
–x I
P
π–x
0
tMFQPJOU2FTUMFTZNÏUSJRVFEF.QBSSBQQPSU
à la droite (OJ ; ils ont donc des abscisses
opposées et des ordonnées égales ;
)
tMF QPJOU 3 FTU MF TZNÏUSJRVF EF . QBS BV
point O ; ils ont donc des abscisses opposées
et des ordonnées opposées ;
J’
tRVBOUBVQPJOU4DFTUMFTZNÏUSJRVFEF.QBSSBQQPSUËMBESPJUF d (que l’on
appelle première bissectrice du repère), dont l’équation est y = x ; l’abscisse
de S est égale à l’ordonnée de M et l’ordonnée de S est égale à l’abscisse de M.
Conséquence
왘
Exemple 1
Cette connaissance des liens entre les sinus et les cosinus de différents angles va
nous permettre de résoudre certaines équations dans lesquelles l’inconnue ﬁgure
dans un sinus ou un cosinus.
Résoudre les équations suivantes :
)
a. cos ( x = 0, 5.
)
c. cos ( x =
Solution
5
.
2
)
b. sin( x = −1.
2
d. sin( x = − .
3
)
π
.
3
Mais on sait que ce n’est pas la seule, puisqu’un point du cercle trigonométrique
correspond à une inﬁnité de réels.
π
Tous ces réels qui correspondent au même point que conviennent, à savoir :
3
π
π
π
π
π
π
+ 2π ,
+ 4 π , + 6 π , … etc. − 2π , − 4 π , − 6 π , … etc.
3
3
3
3
3
3
Mais il y a encore d’autres solutions !
a. Une solution de cette équation, que l’on doit connaitre par cœur, est x =
En effet on a vu précédemment que x et − x ont le même cosinus.
π π
π
π
π
π
π
Donc − , − + 2π , − + 4 π , − + 6 π , … etc. − − 2π , − − 4 π , − − 6 π ,
3 3
3
3
3
3
3
… etc, sont aussi des solutions.
On peut maintenant constater que l’on a toutes les solutions, car il n’y a que deux
points du cercle trigonométrique qui ont la même abscisse.
On résume ces résultats en disant que les solutions sont tous les nombres réels
de la forme :
π
π
+ k 2π ou − + k 2π avec k ∈.
3
3
Séquence 4 – MA12
63
© Cned - Académie en ligne
π
b. Une solution de cette équation, que l’on doit connaître par cœur, est x = − .
2
Mais on sait que ce n’est pas la seule, puisqu’un point du cercle trigonométrique
correspond à une inﬁnité de réels.
π
Tous ces réels qui correspondent au même point que − conviennent, à savoir :
2
π
π
π
π
π
π
− + 2π , − + 4 π , − + 6 π , … etc. − − 2π , − − 4 π , − − 6 π , … etc.
2
2
2
2
2
2
On peut maintenant constater que l’on a toutes les solutions, car il n’y a qu’un
point du cercle trigonométrique dont l’ordonnée soit égale à −1.
On résume ces résultats en disant que les solutions sont tous les nombres réels
de la forme :
π
− + k 2π avec k ∈.
2
5
ne fait pas partie des valeurs « remarquables » des sinus ou
2
cosinus, que l’on doit connaître.
c. La valeur
Pour chercher une solution de cette équation, il faut tout d’abord que l’on ait une
5
, pour savoir si ce nombre est l’abscisse d’un
idée d’une valeur approchée de
2
point du cercle trigonométrique. Si ce n’est pas le cas il n’y aura pas des solution.
5
≈ 1,12.
2
On constate que ce nombre est strictement supérieur à 1. Ça ne peut donc pas
être l’abscisse d’un point du cercle trigonométrique.
On a :
)
Donc l’équation cos ( x =
5
n’a pas de solution.
2
2
d. La valeur − ≈ −0, 67 ne fait pas partie des valeurs « remarquables » des
3
sinus ou cosinus, que l’on doit connaître.
J
π
I’ π−α
N
0
α
2
–—
3
J’
0
I
2
Comme −1 < − < 1 on sait que l’on va trouver deux
3
2
points du cercle trigonométrique dont l’ordonnée est − .
3
Appelons M et N ces points, et F une valeur en radian de
l’angle OI, OM (voir graphique ci-contre).
(
)
2
Cette valeur F est une solution de l’équation sin( x = − .
3
M
On peut, à l’aide de la calculatrice par exemple, trouver une
 2
valeur approchée de cette solution : α = sin−1  −  ≈ −0, 73.
 3
Mais on sait que ce n’est pas la seule solution, puisqu’un point du cercle
trigonométrique correspond à une inﬁnité de réels. Tous ces réels qui
correspondent au même point que F conviennent, à savoir :
α + 2π , α + 4 π , α + 6 π , … etc. α − 2π , α − 4 π , α − 6 π , … etc.
64
© Cned - Académie en ligne
Séquence 4 – MA12
)
Mais il y a encore d’autres solutions.
En effet on a vu précédemment que x et π − x ont le même sinus.
Donc π − α , π − α + 2π , π − α + 4 π , π − α + 6 π , … etc, π − α − 2π ,
π − α − 4 π , π − α − 6 π , … etc, sont aussi des solutions.
On peut maintenant constater que l’on a toutes les solutions, car il n’y a que deux
points du cercle trigonométrique qui ont même ordonnée.
On résume ces résultats en disant que les solutions sont tous les nombres réels
de la forme :
α + k 2π ou π − α + k 2π avec k ∈.
En généralisant les résultats de l’exemple ci-dessus, on peut énoncer la propriété
suivante.
Propriété 13
)
)
Pour résoudre dans une équation de la forme cos ( x = a ou sin( x = a
il faut d’abord vériﬁer si −1 ≤ a ≤ 1.
Si ce n’est pas le cas, l’équation n’a pas de solution.
Si c’est le cas, il y a des solutions.
Pour les trouver toutes, on cherche d’abord une solution particulière α.
)
)
)
)
L’équation peut alors s’écrire : cos ( x = cos ( α ou sin( x = sin( α et l’on a :
)
) ⇔ x = α + 2k π ou x = −α + 2k π ;
sin( x ) = sin( α ) ⇔ x = α + 2k π ou x = π − α + 2k π.
cos ( x = cos ( α
C
Exercice 1
Exercices d’apprentissage
Déterminer si les afﬁrmations suivantes sont vraies ou fausses ; justiﬁer votre
réponse.
 2π 
 π
 5π 
 5π 
� sin   = 2sin  
 3
 3
� cos   = sin  
 4
 4
 5π 
3
� sin   =
2
 3
 7π 
 π
� sin   = − sin  − 
 6
 6
V
F
V
F
V
F
V
F
Séquence 4 – MA12
65
© Cned - Académie en ligne
(
) ( )
� Pour tout réel x, sin( 5π − x ) = sin( x )
� Pour tout réel x, cos x + 5π = cos x
( )
( )
� Pour tout réel x, cos ( 2π − x ) = − cos ( x )
� Pour tout réel x, sin x − π = − sin x
V
F
V
F
V
F
V
F
Pour les deux afﬁrmations suivantes, A, B et C sont trois points distincts.
� BA, CA = − AB, AC + 2k π
V
F
쐅 AB, CA = AB, AC + π + 2k π
V
F
Pour les deux afﬁrmations suivantes, u et v sont deux vecteurs non nuls.
쐈 u , − v = −u , v + 2k π
V
F
쐉 π − u , v = −v , u + 2k π
V
F
(
(
) (
) (
(
) ( )
( ) ( )
)
)
Exercice 2
Soit x un réel. Écrire chacune des expressions suivantes uniquement en fonction
de cos ( x ou sin( x .
Exercice 3
� Conversion degrés-radians ; compléter le tableau suivant :
)
)
� cos ( π − x ) + cos ( x + 3π ).
� sin( − x ) − sin( 3π + x ).
� cos ( − π − x ) − sin( x − 3π ) + sin( 4 π − x ).
9π
2
Mesures en radians
Mesures en degrés
−
13 π
6
−47 π
8
225
−144
50
100
� Donner la mesure principale des angles orientés suivants :
21π 19 π 37 π
−
6
2
4
Mesures
−
29 π
5
100 π
3
−47 π
8
Mesures principales
Exercice 4
π 
3
et que α ∈  , π  . Calculer cos ( α .
5
2 
1
� On sait que cos (β = − et que β ∈  − π , 0  . Calculer sin(β .
3
( )
� On sait que sin α =
)
66
© Cned - Académie en ligne
Séquence 4 – MA12
)
)
50
Exercice 5
Résoudre les équations suivantes et représenter les solutions sur un cercle
trigonométrique.
( )
2
� 2sin2 ( x ) = − sin( x ). Remarque : la notation sin2 ( x ) signiﬁe ( sin( x )) .
� 2 cos ( 2x ) = −1.
� 2cos x + 3 = 0.
Exercice 6
3π
3π
+ 2k π.
On donne u , v = − + 2k π et u , w =
5
4
Déterminer les mesures principales des angles suivants.
( )
( )
(
� v,w .
Exercice 7
( )
)
(
� −u , v .
)
� u,−w .
On considère une ﬁgure où ABC est un triangle rectangle isocèle en A, ACE un
triangle rectangle isocèle en E et BCD un triangle équilatéral.
Les triangles ABC, ACE et BDC sont directs.
� Faire une ﬁgure correspondant à l’énoncé.
� Donner les mesures principales des angles orientés suivants :
a. BC, BA
d. CD, CE
(
(
Exercice 8
)
)
b. AC, AB
e. CA, DC
c. AB, AE
f. AB, CE
)
)
(
(
(
(
)
)
5π
+ 2k π.
ABCD est un parallélogramme tel que AB, AD =
8
� Faire une ﬁgure correspondant à l’énoncé et donner une mesure des angles
orientés suivants :
b. BC, BA
a. BC, DC
)
(
(
)
(
)
On suppose en plus que ABCD est un losange.
� Faire une nouvelle ﬁgure correspondant à l’énoncé et donner une mesure des
angles orientés suivants :
a. CA, CD
(
Exercice 9
)
b. DC, BD
(
c. CA, AD
)
(
)
3π
+ 2k π
A, B et C sont trois points du plan tels que BC, BA =
7
2π
et CA, CB =
+ 2k π.
9
(
(
)
)
� Faire une ﬁgure correspondant à l’énoncé et donner les mesures principales
des angles orientés suivants :
b. CA, BC
a. AB, AC
(
)
(
)
c. BC, AB
(
)
Séquence 4 – MA12
67
© Cned - Académie en ligne
Exercice 10
ABCD et AMCN sont deux parallélogrammes.
Faire une ﬁgure correspondant à l’énoncé et comparer les angles orientés
MA, MB et NC, ND .
(
Exercice 11
) (
)
Démonstration de la propriété 11 du cours : angle inscrit, angle au centre.
Soit deux points distincts A et B d’un cercle de centre O.
Soit M un point du cercle, distinct de A et B, et N le point diamétralement
opposé à M sur ce cercle.
� Quelle est la nature du triangle AOM ?
En déduire que : 2 × MA, MO = π − OM, OA + 2k π.
Puis que : 2 × MA, MO = OA, ON + 2k π.
� De façon analogue, montrer que : 2 × MB, MO = OB, ON + 2k π.
� En déduire que : 2 × MA, MB = OA, OB + 2k π , ce qui démontre la propriété
du cours.
(
(
) (
)
)
) (
(
)
(
(
) (
)
� Question complémentaire, pour aller un peu plus loin.
)
1 Peut-on en déduire que : MA, MB = OA, OB + 2k π ?
2
Quelle propriété peut-on en déduire pour tous les points de l’un des arcs de cercle
?
AB
(
68
© Cned - Académie en ligne
Séquence 4 – MA12
) (
)
3
2
A
Synthèse de la partie 2
de la séquence
Cercle trigonométrique et angles
orientés. Radian
Définition 1
Le radian est l’unité de mesure des angles orientés telle qu’un angle plat
direct mesure π radians.
On le note rad.
Propriété 2
π
Comme π rad = 180 , on a l’égalité 1 =
rad, et donc :
180
π
a =
a rad.
180
°
°
 180 
 180 
x .
Réciproquement, 1 rad = 
, et donc : x rad = 
 π 
 π 
B
Angle orienté de vecteurs non
nuls. Mesure principale
Définition 3
La donnée de deux
vecteurs
non
nuls
u
v
et
, dans cet ordre, détermine un
angle orienté u , v .
On déﬁnit les mesures en radians de l’angle orienté u , v en référence au
cercle trigonométrique.
( )
( )
Propriété 4
Un angle orienté u , v a une inﬁnité de mesures en
radians.
Si l’une des mesures en radians de l’angle orienté u , v est α, les autres
( )
( )
mesures sont tous les nombres de la forme α + 2k π avec k ∈.
Parmi toutes les mesures en radians de l’angle orienté u , v on appelle
mesure principale de l’angle celle qui appartient à l’intervalle  − π ; π  .
( )
Séquence 4 – MA12
69
© Cned - Académie en ligne
Propriétés 5
Quels que soient les vecteurs non nuls u , v et w on a :
a. u , u = 0 + 2k π et u , − u = π + 2k π ;
( )
( )
b. (v , u ) = − (u , v ) + 2k π ;
c. (u , v ) + (v , w ) = (u , w ) + 2k π ; c’est ce que l’on appelle la relation de
Chasles pour les angles orientés ;
d. u , − v = −u , v = u , v + π + 2k π.
) (
(
C
) ( )
Angle orienté de vecteurs
et configurations de base
Propriété 6
Trois points distincts A, B et C sont alignés si et seulement si :
CA , CB = 0 + 2k π ou CA , CB = π + 2k π.
(
)
)
(
Propriété 7
Quatre points distincts A, B, C et D étant donnés, les droites (AB) et (CD)
sont parallèles si et seulement si :
AB, CD = 0 + 2k π ou AB, CD = π + 2k π.
(
)
)
(
Propriété 8
Quatre points distincts A, B, C et D étant donnés, les droites (AB) et
π
(CD) sont orthogonales si et seulement si : AB, CD = + 2k π ou
2
π
AB, CD = − + 2k π.
2
(
)
(
)
Propriété 9
)
Etant donnés trois points distincts A, B et C, la droite ( AK est bissectrice de
si et seulement si : AB, AK = AK , AC + 2k π.
BAC
(
70
© Cned - Académie en ligne
Séquence 4 – MA12
) (
)
Propriété 10
Etant donnés trois points distincts A, B et C, on a :
AB, AC + BC, BA + CA , CB = π + 2k π.
(
)(
)(
)
Propriété 11
Soit deux points distincts A et B d’un cercle de centre O.
Pour
distincts de A et B, on a :
tout
point Mdu
cercle,
OA , OB = 2 × MA , MB + 2k π.
(
D
)
(
)
Cosinus et sinus d’un angle
orienté quelconque
Définition 4
Le cosinus et le sinus d’un angle orienté u , v dont une mesure en
radians est x, sont le cosinus et le sinus du nombre x, c’est-à-dire l’abscisse
et l’ordonnée du point M du cercle trigonométrique correspondant à x.
( )
Propriété 12
Pour tout réel quelconque x :
Mesure en radians
de l’angle
−x
π−x
cos ( − x = cos ( x
)
)
sin( − x ) = − sin( x )
cos ( π − x = − cos ( x
Mesure en radians
de l’angle
x +π
Cosinus
cos ( x + π = − cos ( x
)
Sinus
sin( x + π = − sin( x
)
Cosinus
Sinus
)
)
sin( π − x ) = sin( x )
)
)
π
−x
2
π

cos  − x  = sin( x
2

)
)
π

sin  − x  = cos ( x
2

Séquence 4 – MA12
71
© Cned - Académie en ligne
Propriété 13
)
)
Pour résoudre dans une équation de la forme cos ( x = a ou sin( x = a
il faut d’abord vériﬁer si −1 ≤ a ≤ 1.
Si ce n’est pas le cas, l’équation n’a pas de solution.
Si c’est le cas, il y a des solutions.
Pour les trouver toutes, on cherche d’abord une solution particulière α.
L’équation peut alors s’écrire : cos ( x = cos ( α ou sin( x = sin( α et l’on a :
)
)
)
) ⇔ x = α + 2k π ou x = −α + 2k π ;
sin( x ) = sin( α ) ⇔ x = α + 2k π ou x = π − α + 2k π.
cos ( x = cos ( α
72
© Cned - Académie en ligne
Séquence 4 – MA12
)
)
4
Exercices
d’approfondissement
Exercice I
Sans utiliser la calculatrice, calculer les nombres suivants.
 π
 3π
 5π
 7π
A = cos   + cos   + cos   + cos   .
 8
 8 
 8 
 8 
 9π
 11π 
 π
 2π 
 3π
B = cos   + sin   + cos   + sin   + cos 
 100 
 10 
 10 
 5
 5 
 7π
 8π
 19 π 
+ sin   + cos   + sin 
.
 5
 5 
 10 
 2π 
 4π
 6π
 8π
C = sin   + sin   + sin   + sin   .
 5
 5 
 5 
 5 
 π
 3π
 5π
 7π
D = cos2   + cos2   + cos2   + cos2   . On rappelle que cos2 ( x
 8
 8 
 8 
 8 
(
signiﬁe cos ( x
Exercice II
))2 .
Résoudre les équations suivantes et représenter les solutions sur un cercle
trigonométrique.
�
( )
)
2 sin( x − 1 = 0.
( )
� 2cos2 x + 3cos x + 1 = 0.
( )
( )
( )
� 2sin2 x + cos x = 2.
� cos 3x = 0.
Exercice III
)
 π
6+ 2
.
On admet que cos   =
4
 12 
� Calculer :
 π
a. cos  − 
 12
 11 π 
b. cos 
 12 
 π
� Montrer que : sin   =
 12 
� Calculer :
 π
a. sin  − 
 12
 13 π 
c. cos 
 12 
 35 π 
d. cos 
 12 
6− 2
.
4
 11 π 
b. sin 
 12 
 13 π 
c. sin 
 12 
 35 π 
d. sin 
 12 
Séquence 4 – MA12
73
© Cned - Académie en ligne
Exercice IV
π
On considère un carré ABCD direct, c’est-à-dire tel que AB, AD = + 2k π. On
2
construit les triangles ABE et BFC équilatéraux et directs.
)
(
� Faire une ﬁgure correspondant à l’énoncé et donner les mesures principales
des angles orientés suivants :
a. AE, AD
b. BC, BE
)
(
(
c. CD, CF
)
(
)
� En déduire les mesures principales des angles orientés des triangles ADE, BCE
et CDF.
(
)
� a. Déterminer la mesure principale de l’angle orienté EC, ED .
b. En déduire la mesure principale de l’angle orienté DE, DC .
� a. Comparer cette mesure avec celle de l’angle orienté DF, DC trouvée au �.
b. Qu’en déduit-on pour les points D, E et F ?
(
Exercice V
(
)
)
Propriété établie en ﬁn de l’exercice 11 : soit deux points distincts A et B d’un
cercle de centre O. Pour
tout
point M de l’un des arcs de cercle AB, distinct de A
et B, l’angle orienté MA, MB est constant.
)
(
Dans cet exercice, nous allons établir la propriété réciproque, à savoir : deux
points distincts A et B du plan, et un réel non nul α tel que α ∈  − π ; π  étant
donnés, l’ensemble des points M du plan tels que MA, MB = α est un arc de
cercle AB.
(
)
On considère donc deux points distincts A et B du plan, et un réel non nul α tel
que α ∈  − π ; π  .
On considère un point M du plan tel que MA, MB = α.
)
(
� a. Construire le centre K du cercle circonscrit au triangle ABM.
b. En déduire que ce centre est indépendant du choix du point M.
� En déduire que tout point N tel que NA, NB = α est nécessairement sur le
cercle de centre K passant par A.
� Montrer que sur ce cercle seuls les points d’un des deux arcs de cercle AB
(
)
conviennent.
Exercice VI
Au cours d’une méharée dans le désert, un aventurier égaré et dont le GPS est
en panne ne dispose que d’un instrument lui permettant de mesurer les angles
suivant lesquels il voit deux points.
Il reconnaît autour de lui deux pics rocheux, notés P et R sur sa carte, et un arbre
mythique noté M.
� Déterminer le point A où se trouve l’aventurier, sachant qu’il a mesuré que :
π
π
AR, AP = + 2k π et AM, AR = + 2k π.
3
4
� Construire ce point A sur la ﬁgure ci-après représentant la carte de notre
aventurier.
(
74
© Cned - Académie en ligne
Séquence 4 – MA12
)
(
)
P
M
R
■
Séquence 4 – MA12
75
© Cned - Académie en ligne