Sujet du TP

TP modélisation récupération énergie
M.D. 2015
1
3A EMS
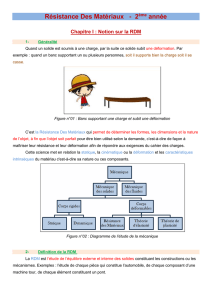
RECUPERATION D’ENERGIE DE VIBRATION
Modélisation et simulation
Objectifs :
 Utiliser l’environnement Scilab/Xcos pour la modélisation et la simulation haut niveau d’un système
complet de récupération d’énergie de type piézoélectrique
 Dimensionner le système pour l’adapter à une fréquence de vibration donnée
1. Présentation du sujet
1.1 Présentation de la structure étudiée
Le système étudié est un système de récupération d’énergie de vibration de type piézoélectrique.
Il se présente sous forme d’une poutre encastrée à
l’une de ses extrémités et surmontée d’une masse à
son autre extrémité.
Vue de coté du système de récupération d’énergie
La poutre est constituée d’un matériau support (cale) et de deux couches
de matériau piézorésistif.
Vue section de la poutre
1.2 Théorie et fonctionnement des (micro-)systèmes de récupération d’énergie de vibration
Les systèmes de récupération d’énergie de vibration reposent sur la
conversion de l’énergie mécanique d’une masse mobile en énergie
électrique. Le système mécanique peut être modélisé en première
approche par un système mécanique du second ordre de type masse-
ressort amorti illustré ci-contre.
Avec m la masse de la masse mobile, k la constante de raideur du
ressort, be et bm les amortissements.
On distingue bm, l’amortissement mécanique -lié au frottement
visqueux lors du déplacement, aux pertes dans les couches de
matériaux et à leurs interfaces- de be, l’amortissement électrique dû à
la conversion d’énergie mécanique en énergie électrique.
Système mécanique du second ordre
amorti.
1.2.1 Rappel système mécanique du second ordre

TP modélisation récupération énergie
M.D. 2015
2
Le système mécanique est alors représenté par l’équation du mouvement :
extme ymkyy)bb(ym  
ext
y
représente l’accélération des vibrations extérieures agissant sur le système masse-ressort.
La transformée de Laplace (voir annexe) permet d’écrire :
kp)bb(mp
)p(Ymp
)p(Y me
2ext
2
Expression de la puissance électrique convertie :
La force électrique due à l’amortissement est :
y.bF ee 
La puissance électrique moyenne convertie lors du déplacement de la masse s’écrit :
2
ey.F
2
1
P
(
2
e
v
0
evb
2
1
dvvbP  
)
On adopte les notations :
nee m2b 
;
nmm m2b 
;
m/k
2
n
et
met 
pour exprimer la
puissance convertie en fonction de l’accélération des vibrations. Les termes
e
et
m
sont
respectivement les rapports d’amortissement équivalents électrique et mécanique.
)(Y
12
m
)(P 2
2
2
n
2
n
t
3
n
6
e
Dans le cas d’un système résonant et d’une fréquence de vibration correspondant à cette résonance, la
puissance convertie devient :
)(Y
4
m
)(P n
2
2
t
3
ne
n
Soit finalement :
)(A
4
m
)(P n
2
n
2
t
e
n
La puissance convertie est maximum pour
me 
et vaut :
)(A
16
m
)(P n
2
nm
max
n
Analyse de cette formule :
P ~ masse
P ~ a2
P ~ 1/f
1.2.2 Paramètres du modèle masse-ressort en fonction de la géométrie et des matériaux
Ce paragraphe concerne le lien entre la géométrie et les matériaux du système poutre-masse et le
modèle masse-ressort.

TP modélisation récupération énergie
M.D. 2015
3
En première approximation la masse de la poutre est négligée par rapport
à la masse utile en bout de poutre qui est elle considérée ponctuelle. On
modélise alors le système par une poutre soumisse à une force à son
extrémité (voir Annexe).
La raideur k du ressort du modèle du 2nd ordre masse-ressort est alors :
3
L
YI3
k
avec L la longueur de la poutre, Y le module d’Young du matériau constituant la poutre et I le moment
d’inertie quadratique de la poutre (cf Annexe) valant ab3/12.
1.2.3 Conversion de l’énergie mécanique de type piézoélectrique
Trois principes de conversion peuvent être mis en œuvre : électromagnétique, piézoélectrique et
électrostatique.
Ce paragraphe et ce sujet se focalisent sur la conversion de type piézoélectrique.
Le principe repose sur l’effet piézoélectrique direct correspondant à la polarisation électrique sous
l’action d’une contrainte.
Les équations de la piézoélectricité sont :
dED
dE
Y
avec :
δ : déformation mécanique (strain) [m]
σ : contrainte mécanique (stress) [N/m2]
ε : constante diélectrique [C.V-1.m-1]
d : coefficient piézoélectrique de déformation [m/V]
Y : module d’Young [N/m2]
E : champ électrique [V/m]
D : déplacement électrique [C/m2]
Le système mécanique piézoélectrique est
connecté à une circuit électronique en
aval représenté par une résistance de
charge RL
La présence de 2 couches de matériau piézoélectrique
permet de doubler la réponse électrique à la déformation
mécanique.
Dans l’exemple de la figure, la couche supérieure
de matériau piézoélectrique subit une contrainte
en extension, la couche inférieure une contrainte
en compression
La charge à la surface des matériaux piézoélectrique s’exprime par :
L.a.D2q 
Le facteur 2 traduit le doublement de la réponse électrique par l’association en parallèle des couches
piézoélectriques.
La tension entre les surfaces des couches piézoélectrique est :
p
t.EV 
avec tp l’épaisseur de la couche piézoélectrique.
Alors :
.L.a.Y.d.2q
t
dYV
p
Géométrie de la poutre :
 longueur L,
 largeur a,
 épaisseur b

TP modélisation récupération énergie
M.D. 2015
4
La variation de charge, donc le courant, et la tension au niveau des surfaces des couches
piézoélectriques sont ainsi exprimées en fonction de la déformation et de la contrainte.
On peut finalement, voir annexe, la puissance transférée à une charge RL :
2
in
2
mnpL
2
piézom
2
npL
4
piézo
2
m
2
*
piézopiézo
2
pL
2
n
nA
4CRk4CRk4
a
bdtY2
CR
1
P
avec
piézo
2
2
piézo Yd
k
le coefficient de couplage piézoélectrique.
En dérivant l’expression de la puissance transférée à la charge en fonction de RL, on peut obtenir la
valeur de résistance de la charge optimale.
42
m
m
p
Lk42
2
C
1
Ropt 
La puissance optimale transférée dans le cas de la charge Ropt est alors :
2
in
4
piézo
2
m
2
piézom
2
*
piézopiézo
P
3
n
nA
k4k4
a
bdtY2
C
1
P
avec :
la permittivité du matériau piézoélectrique,
Ypiézo le module d’Young du matériau piézoélectrique,
d le coefficient piézoélectrique de déformation,
piézo
2
2
piézo Yd
k
le coefficient de couplage piézoélectrique,
piézo
piézopiézo
Pt
lw2
C
la capacité des deux couches piézoélectrique associées en parallèle,
tpiézo l’épaisseur des couches de matériau piézoélectrique,
m
le rapport d’amortissement équivalent mécanique,
mb
emb
2
b
b
*
l
2
3
l2
lll2
l
b3
b
le coefficient reliant la déformation moyenne des fibres du matériau
piézoélectrique au déplacement vertical de la poutre
schéma de définition des longueurs de la poutre lb, de la masse lm et des électrodes
le (inférieure ou égale à lb)
schéma de définition des dimensions de
la section de la poutre
Remarque : le rapport d’amortissement équivalent électrique
e
s’écrit lui :
2
pL
2
2
cp
e
CR
1
2
k

TP modélisation récupération énergie
M.D. 2015
5
2. Environnement Scilab/Xcos
La simulation numérique est incontournable lors de la conception de systèmes. Simuler les
phénomènes éventuellement multi-physiques (électronique, mécanique, thermique,…) permet d’en
étudier le comportement et d’obtenir des résultats sans avoir à réaliser des prototypes et des
expérimentations. Les logiciels de simulation sont largement utilisés dans l’industrie et la recherche
pour l’étude, la modélisation et le dimensionnement de systèmes.
Pour ce TP, vous utiliserez le logiciel Scilab
1
, équivalent gratuit et français de Matlab® et de Xcos
l’outil de Scilab dédié à la modélisation et à la simulation des systèmes. Vous disposerez de fichiers
préexistants décrits dans ce paragraphe. Les données numériques utilisées sont arbitraires pour illustrer
les comportements du système.
2.1. Modèle du 2nd sous Scilab/Xcos
Rappel : forme canonique du 2nd ordre :
2
n
2
n
p
p
2
1
K
)p(H
avec p la variable de Laplace, K le gain statique,
n
la pulsation naturelle du système et le
coefficient d’amortissement.
2.2. Description des fichiers Scilab et Xcos existants
Le répertoire de travail comporte un fichier pour Xcos Modele2ndOrdre.zcos et un fichier script
Modele2ndOrdre.sce.
 Modele2ndOrdre.zcos contient la modélisation graphique d’un système du 2nd ordre par sa fonction
de transfert canonique en notation de Laplace. Ce fichier permet à partir des paramètres du système
mécanique d’observer le signal temporel de sortie du système soumis à un signal d’entrée.
 parametreSimulationXcos.sce contient les paramètres de la modélisation graphique
Modele2ndOrdre.zcos.
ci-dessus : contenu du fichier
Modele2ndOrdre.zcos. ci-contre le fichier script
des paramètres utilisés dans
Modele2ndOrdre.zcos
 Modele2ndordre.sce contient la modélisation
d’un système du 2nd ordre par sa fonction de
transfert canonique en notation de Laplace. Ce
fichier permet à partir des paramètres du
système mécanique d’évaluer les conditions et
fréquence de résonance.
Références bibliographiques
S. Roundy, et al., Energy scavenging for wireless sensor
networks, Kluwer Academic Publisher, (2004)
Scilab pour les vrais debutants
Xcos pour les vrais debutants
1
https://www.scilab.org/
Contenu du fichier Modele2ndOrdre.sce pour la simulation
fréquentielle du modèle du 2nd ordre.