Nombres complexes I L`ensemble C des nombres complexes
 6
6
 7
7
 8
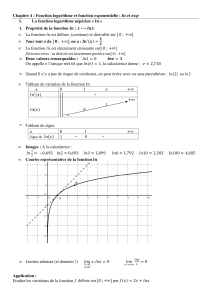
8
 9
9
 10
10
 11
11
1
/
11
100%