Chapitre 3 : Dérivation.

Chapitre 3 : Dérivation.
I - Nombre dérivé, tangente.
Définition : Soit f une fonction et a un réel appartenant à l’ensemble de
définition de f .
 Le taux d’accroissement de f entre a et a + h est le rapport
t(h) = 
(a +h) ∈ Df
 La fonction f est dérivable en a lorsque le taux d’accroissement t(h)
admet comme limite un nombre réel quand h tend vers 0.
Ce nombre, noté f ’(a) ,est appelé nombre dérivé de f en a.
f ‘(a) = 
.
Exemple 1 :
Montrer que la fonction carrée f est dérivable en 2 et que f ’(2) = 4.
∀ h ∈ ℝ*
=  = = 4+h
D’où 
  et donc la fonction carrée f est dérivable en 2 et
f ‘(2) = 4
Définition rigoureuse: Si f est dérivable en a, on appelle tangente à Cf au
point A(a ;f(a)) la droite passant par A et de coefficient directeur f ‘(a).
L’équation réduite de la tangente à Cf en A est :
y =    
Approche historique : ( la tangente est "presque" Cf au voisinage…)
f ‘(a) est le coefficient directeur de la tangente à Cf au point A(a ;f(a))

Exemple 1(suite) : Reprenons la fonction carrée f
(∀ h ∈ ℝ* )
Le réel 
 est le coefficient directeur de la sécante passant par
A(2 ;f(2)) et par M(2+h ;f(2+h))
Sa limite, quand h tend vers 0 est le coefficient directeur de la tangente à
Cf en A.
f'‘(2) est le coefficient directeur de la tangente à Cf en A (2 ;f(2).
II - Fonction dérivée.
A ) Un exemple.
Exemple 1 : Soit f la fonction définie sur ℝ par f(x) = x2
On a vu que f ‘(2) = 4.
Essayons de compléter le tableau de valeurs
x
-2
-1
0
1
2
3
4
f ’(x)
4
Avec des considérations graphiques, compléter quelques valeurs.
(geogebra fonction carrée)
Rappelons que :
f ‘(a) est le coefficient directeur de la tangente à Cf au point A(a ;f(a))
c’est-à-dire au point d’abscisse a.
La courbe de la fonction carrée admet une tangente horizontale au point
d’abscisse 0 donc f ‘(0) = 0.
On peut calculer une à une les valeurs mais on peut aussi essayer de savoir
si il y a une formule.
On avait vu :
∀ h ∈ ℝ*
=  = = 4+h
D’où 
  et donc la fonction carrée f est dérivable en 2 et
f ‘(2) = 4

Soit x0 un réel, calculer f’(x0)
∀ h ∈ ℝ*
=  = =2+h
D’où 
Et donc f ’()= 
On a donc montrer que :
∀ x0 ∈ ℝ , f ‘(x0) = 2x0
Ou encore : ∀ x ∈ ℝ , f ‘(x) = 2x.
On peut donc compléter le tableau de valeurs.
x
-2
-1
0
1
2
3
4
f ’(x)
-4
-2
0
2
4
6
8
On voit que l’on vient de définir une nouvelle fonction appelé fonction
dérivée de f et notée f ‘.
Ici la fonction f ‘ est définie sur ℝ par f ’(x) = 2x.
Remarque : la fonction dérivée f ‘ dépend de la fonction f.
Questionnement et remarques.
Que peut-on dire de la fonction dérivée pour la valeur de x pour laquelle la
fonction f admet un extrémum (mini ou maxi) ?
Peut-on dire des choses en plus ?
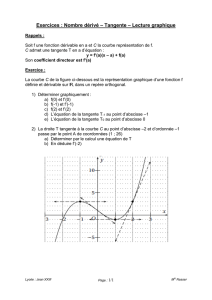
Exercice : Soit f la fonction définie sur ℝ par f(x) = x2 – 5x + 7
La f° dérivée de f est la fonction f ’ définie sur ℝ par f ‘(x) = 2x -5
1) Placer le point de Cf d’abscisse 1 puis la tangente
à Cf en ce point.
Solution : 1°) Le point d’abscisse 1 de Cf a pour ordonnée f(1) =..=2
On place donc le point de coordonnées (1 ;1)
La tangente à Cf au point d’abscisse 1 a pour coefficient
directeur f ‘(1) = 2×1 – 5 = -3.
On trace donc la droite passant par le point de coordonnées (1 ;1) avec un
coefficient directeur 2.
(Localement au voisinage du point en bleu plus des pointillés jusqu’au
2ème point de la tangente)
2) De même pour les points
d’abscisse -1 ;0 ;2 ;3 ;4
3) Tracer la courbe de f.
4) Vrai/ faux. Le minimum
de f est 1 atteint
pour x = 2 et x = 3
On peut voir sur cet exemple que la dérivée de la fonction f nous permet
de deviner que 1 n’est pas le minimum de la fonction f.
J’utilise la rédaction « ou encore »
quand je redis d’une autre façon la
même chose.
Ici, utiliser x0 ou x n’a aucune
importance.

B ) Intérêt.
Exemple d’introduction : Soit f la fonction dont la courbe est donnée ci-
contre.
1) Signe de f
2) Variation de f
Y a-t-il un lien
entre ces deux
tableaux ?
3) Résoudre f ‘(x) = 0
On cherche les valeurs de x tel que f ‘(x) = 0 i.e. tel que le coefficient
directeur de la tangente à Cf au point d’abscisse x soit nul ( tangente
horizontale)
4) Dresser le tableau de signe de f ‘
Y a-t-il un lien avec un tableau précédent ?
Théorème (admis): Soit f une fonction dérivable sur un intervalle I.
 Si pour tout x de I, f ’(x) > 0, alors f est strictement croissante sur I.
 Si pour tout x de I, f ’(x) < 0, alors f est strictement décroissante sur
I.
 Si pour tout x de I, f ’(x) = 0, alors f est constante sur I.
Ex 1: Donner les variations de la fonction f
Tableau de variation de f :
x
-3 -1 2 5 6
f ’(x)
+ 0 - 0 + 0 -
f(x)
Remarque : Ce théorème reste vrai si f ‘ s’annule pour un nombre fini de
valeurs de x.
Ex. 2: Tableau de variation de f :
x
-3 -2 0 1 2 5 6
f ’(x)
+ 0 + 0 + 0 - 0 - 0 +
f(x)
On pourra construire une courbe possible de f
C ) Définition d’une fonction dérivée ; calcul d’une fonction dérivée.
Définition : On dit que la fonction f est dérivable sur un intervalle I
lorsqu’elle est dérivable pour tout réel a de I.
La fonction qui, à tout réel x de I, associe le nombre dérivé de f en x, est
appelée fonction dérivée de f et est notée f ‘.
Fichier Tableau des dérivées :♥ (à connaître par cœur)
Exemples de fonctions dérivées :
Dans chacun des cas suivants, donner l’expression de la dérivée de f sur I
quand f est définie sur I par.
a) f(x) = 3x +5 I = ℝ
Méthode: ♥ Si la fonction est une fonction de référence, on utilise le
premier tableau.
La fonction f est une fonction affine donc est dérivable sur ℝ(Intervalle de
validité) et : pour x réel, f ‘(x) = 3 Règle 2

b) f(x) = x2 I = ℝ
La fonction f est dérivable sur ℝ et : pour x réel, f ’(x) = 2x (3)
c) f(x) = x3 d) f(x) = x5 e) f(x) = x
f) f(x) =
2
1
x
g) f(x) =
x
1
h) f(x) = 5x4
i) f(x) = x4 + 3x I = ℝ
Méthode: Lorsque la fonction n’est pas une fonction de référence, on
décompose la fonction en utilisant le deuxième tableau.
Au brouillon, on reconnaît la forme de f
f(x) = u(x) + v(x) avec
3 (x)v' et xxv
4x (x)u' et x u(x) 34
3)(
La fonction f est dérivable sur ℝ comme
somme de fonctions dérivables sur ℝ
et pour x réel : f ’(x) = 4x3 +3
j) f(x) = x2 +
x
1
I = ℝ *
k) f(x) = 6x5 + 4x3 + 2x2 + 3x +1 I = ℝ
Remarquons que la dérivée d’un somme est la somme des dérivées :
La fonction f est un polynôme (somme de monôme axn) dérivable sur ℝ
et : pour x réel,
f ’(x) = 6 ×5x5-1 + 4×3x3-1 + 2×2x2-1 + 3
f ‘(x) = 30 x4 + 12x2 + 4x + 3
l) f(x) = 2x5 + 6 x3 + 7x2 + 5 m) f(x) = 3x4 – 6x2
n) f(x) = (5x2 + 4) (8x3 + 2) o) f(x) =
5
1x
p) f(x) =
x
1
sur ℝ
+* f’(x) =
xx2
1
q) f(x) =
xx x38 4
2
définie sur ]0 ; + [
r) f(x) =
x
2
sur ℝ *
Démonstration de : (uv)’ = u’v + uv’
p 63.
u + v u’ + v’
x4 + 3x 4x3 +3
On dérive
chaque
monôme