Les triangles congrus - Blogues CSAffluents.qc.ca

Chapitre 3 – La Géométrie Euclidienne École secondaire Félix-Leclerc
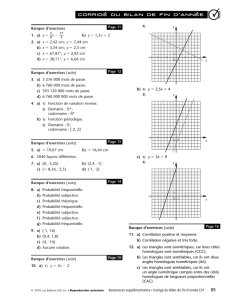
35
Cours 2
Les triangles congrus
En général, des figures congrues (ou isométriques) sont des figures qui ont :
 Tous leurs _____________ homologues _____________
 Tous leurs _____________ homologues _____________
Pour prouver que deux triangles sont isométriques, il n’est pas nécessaire de
démontrer que tous les côtés homologues sont congrus deux à deux, et que tous les
angles homologues sont congrus deux à deux.
On peut utiliser l’un des trois cas de congruence des triangles suivants :
1er cas de congruence :
C – C - C
Si les triangles ont 3 paires de ____________ homologues ______________ ,
alors on peut affirmer que les deux triangles sont isométriques.
Exemples :
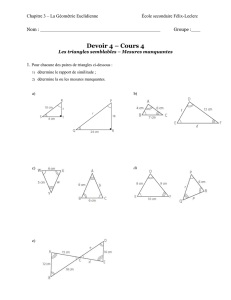
Est-ce que les triangles suivants sont isométriques par le cas de congruence C-C-C?
a)
Réponse : ________
b) ABCD est un parallélogramme.
Réponse : ________
AC
B
6 cm
E
D
F
6 cm
10 cm
8 cm
8 cm
A
C
B
D

Chapitre 3 – La Géométrie Euclidienne École secondaire Félix-Leclerc
36
2e cas de congruence :
C – A - C
Si les triangles ont 1 paire d’ ____________ homologues ______________ ,
compris entre 2 __________ homologues _____________ , alors on peut
affirmer que les deux triangles sont isométriques.
Exemples :
Est-ce que les triangles suivants sont isométriques par le cas de congruence C-A-C?
a)
4 cm
E
F
4,2 cm
A
C
B
D
46°
4 cm 4,2 cm 46°
Réponse : _________
b)
Réponse : _________
c)
Réponse : _________
3 cm
3 cm
35°
35°
8 cm
E
F
8,3 cm
D51°
A
C
B
8 cm 8,3 cm
51°

Chapitre 3 – La Géométrie Euclidienne École secondaire Félix-Leclerc
37
3e cas de congruence :
A – C - A
Si les triangles ont 1 paire de ____________ homologues ______________ ,
compris entre 2 __________ homologues _____________ , alors on peut
affirmer que les deux triangles sont isométriques.
Exemples :
Est-ce que les triangles suivants sont isométriques par le cas de congruence A-C-A?
a)
8 cm
8 cm
Réponse : _________
b) ABCD est un rectangle.
D
A
C
B
Réponse : _________
c)
Réponse : _________
8 cm
8,3 cm
51° 8 cm 8,3 cm
51°
46°
46°