i. nombre derive

DERIVATION 1
I. NOMBRE DERIVE
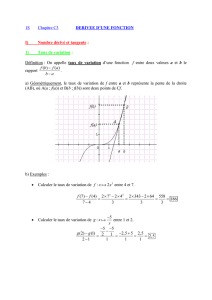
A. Taux d’accroissement :
définition :
exemples :
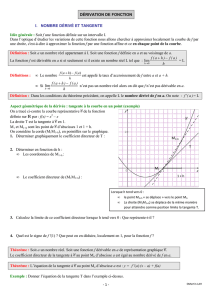
Graphiquement : On considère une fonction f et deux points de la courbe d’abscisses respectives
x1 et x2 :
Le taux d’accroissement est égal au
B. Nombre dérivé :
Définition :
On dit alors que la fonction est :
Remarque : Nous avons vu que le taux d’accroissement d’une fonction affine f(x)=mx+p est
constant et égal à m.

2
C. Tangente :
cas particulier : Pour la fonction carré, le taux d’accroissement f(a+h)−f(a)
h est le coefficient
directeur de la droite ( AM) où A et M sont les points de la parabole d’abscisses respectives a et
a+h .Avec géogébra, nous avons pu observer que la droite ( AM) a une position limite lorsque h se
rapproche de 0. Cette droite est appelée tangente à la parabole au point A, elle a pour
coefficient directeur la limite du taux d’accroissement quand h tend vers 0, c’est-à-dire le
nombre dérivé de f en a.
cas général :
Définition :
Construction : On va savoir tracer rapidement la tangente à une courbe en quelques points ., cela
va permettre de préciser l’allure de la courbe. Il suffit de savoir construire une droite
connaissant un point et son coefficient directeur.
Livre : exercice 9 page 103.
Remarque : Si le nombre dérivé est nul alors :
On peut noter qu’il n’est pas nécessaire de connaître l’équation de la tangente complètement pour
tracer cette droite.
Equation : Parfois, il peut être utile de déterminer l’équation de la tangente, par exemple, pour
étudier la position de la courbe par rapport à cette tangente.
On sait déjà que le coefficient de cette tangente au point d’abscisse a est f ’(a).
Donc l’équation est de la forme : y = f ’(a)x + p.
or cette tangente passe par le point A ( a , f(a) ) donc :
Conséquence :
L’équation de la tangente à la courbe au point d’abscisse a est :
________________________________________________________________________

3
II. FONCTION DERIVEE
A. Définition :
Cas particulier : nous avons vu que la fonction f(x)= x² est dérivable en tout nombre
réel a et que son nombre dérivé en a est 2a.
On peut donc définir une nouvelle fonction :g(a)=2a ou g(x)=2x .
Comme 2a est le nombre dérivé de f en a , on appelle cette fonction : fonction
dérivée de f et on la note : f ’ . Ainsi pour tout nombre réel x, on a f ’(x)=2x.
B. Dérivée des fonctions usuelles :
Exemples :
Fonction affine : f(x)=mx +p :
Fonction constante : f(x) =k :
Tableau des dérivées des fonctions usuelles :
f(x)
f ’(x)
Ensemble de définition
f(x)=k
f(x)=x
f(x)=x²
f(x)=x 3
f(x)=x n
f(x)=1
x
C. Opérations sur les fonctions dérivables : Dans ce paragraphe, u et v sont deux
fonctions définies et dérivables sur un même intervalle I.
Somme :
Théorème : u + v est dérivable et ( u + v )’ = __________________________ .
Exemple : déterminer la fonction dérivée de f(x)=x² + 1
x définie sur [1 ; 10].
Produit par une constante k :
Théorème : ku est dérivable et ( ku )’ = _____________________________ .
Exemple : déterminer la fonction dérivée de f(x)=5
2(x + 1 x ) définie sur ]0 ; +∞[.

4
Conséquence : Dérivée d’une fonction polynôme :
Déterminer la dérivée de f(x)=2x 4 +5x 3 – 7x² +3x +19 définie sur ℝ .
Produit de deux fonctions :
Nous admettrons le résultat suivant :
Théorème : uv est dérivable et
Exemple : déterminer la fonction dérivée de f(x)=( 2x + 3 )(1–3x) définie sur ℝ .
Dérivée de u² :
Théorème : u ² est dérivable et
Déterminer la dérivée de f(x)=(2x – 5 )² définie sur ℝ .
Inverse :
Nous admettrons le résultat suivant :
Théorème : Si pour tout x de I on a v(x)≠ 0 , alors 1
v est dérivable et
Déterminer la fonction dérivée de f(x)= 1
2x +7 définie sur [0 ; 10].
Quotient :
Nous admettrons le résultat suivant :
Théorème : Si pour tout x de I on a v(x)≠ 0 , alors u
v est dérivable et
Déterminer la fonction dérivée de f(x)=2x – 3
3x +1 définie sur [0 ; 10].

5
III. Lien entre signe de la dérivée et sens de variation.
A. Fonction constante sur un intervalle :
Théorème : Si f est dérivable sur un intervalle I et si la dérivée f ’est nulle sur I ,
alors la fonction est constante sur I.
B. Fonction dérivable et monotone sur I :
L’observation du coefficient directeur de la tangente à partir d’exemples, nous a
permis de déduire les résultats suivants :
Théorème 1 : Si f est dérivable sur un intervalle I et si la dérivée f ’est
sur I , alors la fonction est sur I.
Théorème 2 : Si f est dérivable sur un intervalle I et si la dérivée f ’est
sur I , alors la fonction est sur I.
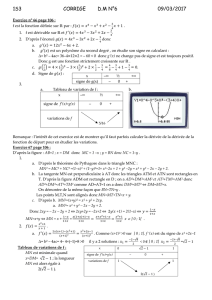
Exemple : On se propose d’étudier le sens de la fonction f définie sur [ –3 ; 2 ] par :
f(x)=x 3 –3x + 2 .
Les variations de f sont présentées dans son tableau de variation :
x
– 3 –1 1 2
Signe de f ’(x)
Variation de f
Ce tableau permet de déterminer un éventuel maximum ou minimum de cette fonction
et éventuellement son signe.
Tous ces résultats sont extrêmement importants et vont être l’objet de
nombreux problèmes au cours de l’année.