une probabilite etonnante sur la taille de la plus longue suite

1
L’ ETONNANTE PROBABILITE DU PLUS PROBABLE NOMBRE MAXIMUM DE RESULTATS
CONSECUTIFS IDENTIQUES LORS D’UNE SUITE DE LANCERS D’UNE PIECE BIEN EQUILIBREE
J F Kentzel - Lycée Pardailhan à Auch (32) - [e-mail]
Remerciements à Anne Bauval (Université de Toulouse).
Sans elle, la preuve des résultats qui suivent serait restée trop longue et quasiment illisible.
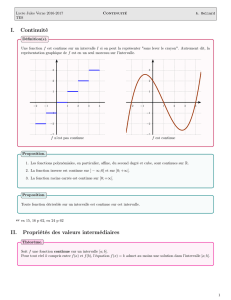
1 ) INTRODUCTION
Faire un quelconque pari sur la valeur prise par une variable aléatoire dépendant de la suite des résultats obtenus en lançant une
pièce de monnaie, supposée bien équilibrée, peut sembler a priori ne pas être raisonnable, par exemple si on lance
mn 2
fois
une pièce (on a un résultat proche si
n
est impair) et si on appelle
n
F
la variable aléatoire « nombre de « face » obtenus », on
sait que la valeur la plus probable de
n
F
est
m
, c'est-à-dire que le maximum des
kFP n
est obtenu pour
mk 
et
vaut
n
n
n
2
1
.
2
=
m
m
m
2
21
.
2
. Jouer en pariant que
3
6F
, par exemple, est possible puisque
3125.0)3( 6FP
mais
la formule de Stirling, si
n
est grand,
n
e
n
nn  2!
, montre que :
2/nFP n
vaut environ
2//1 n
pour
n
assez grand.
Les plus grandes probabilités « s’évanouissent » quand
n
grandit.
Il existe cependant un pari donnant une chance non négligeable de gagner pour toute valeur de
n
: il suffit
de parier sur la valeur de la variable aléatoire, qu’on désignera par
n
L
: la longueur de «la» plus longue
suite de résultats consécutifs identiques obtenue à l’issue du
n
-ième lancer d’une pièce équilibrée.
Notations : dans ce qui suit
)(xEnt
est la partie entière d’un réel
x
et
xLn
le logarithme népérien de
x
.
On désigne par
C
le nombre
))15/(2(.2 Ln
qui vaut environ 0,962.
Poser
C
c1
)04,1( c
serait pratique pour les deux lignes qui suivent mais ne le serait pas du tout ensuite.
En prenant le risque de chagriner les lecteurs pointilleux, on s’autorise dans ce qui suit l’écriture incorrecte
kFP n
au
lieu de
kFP nn 
(écriture qui rappelle que pour chaque valeur de
n
on a un univers et une loi de probabilité différents
mais n’apporte rien au fond).
On va voir qu'on a environ une chance sur quatre
1
de gagner en pariant sur le nombre
)2/)/(( LnCnLnEnt
. On obtient des chiffres tout aussi étonnants lorsqu’on parie sur la valeur
de
n
L
dans un intervalle contenant deux, trois quatre…valeurs entières, voir le commentaire 4.
Si on trouve ce résultat trop compliqué, on peut remplacer par le nombre
)2/)((' LnnLnEnt
. On a alors des
résultats presque aussi bons
2
. On va garder le nombre dans ce qui suit car il va apparaître naturellement.
2 ) GENERALITES SUR LA LOI DE Ln
Notons d’abord qu’on peut, en théorie, calculer la loi de
n
L
pour toute valeur de
n
:
Soit
k
un entier fixé,
nk 1
. En désignant par
)(k
n
E
l’événement :
1
Plus précisément : on gagne avec au moins la probabilité
236,025 
.
2
Par rapport au résultat précis qu’on peut énoncer avec , on perd environ la probabilité 0,0053. Par ailleurs et
'
sont
« souvent » égaux car
2/2/)(2/)/( LnCLnLnnLnLnCnLn 
qui vaut environ 0,056. Anecdotiquement ,
'
est, à une unité près, le nombre de chiffres de
n
en base 2 mais je n'ai aucune interprétation de cette coïncidence. Je n’ai pas
non plus d’interprétation autre que simpliste du fait que multiplier
n
par 2, c’est ajouter 1 à
'
.

2
{il existe (au moins) une suite de
k
résultats consécutifs égaux à l’issue du
n
ième lancer} et en notant
)(k
n
p
pour
)( )(k
n
EP
, on prouve facilement que la suite
)(k
p
=
1
)( )( n k
n
p
est définie par :
Si
1 kn
,
0
)(  k
n
p
;
1
)( 21
k
k
k
p
;
Si
1 kn
,
)()( 1 )( 1
2
1kkn
k
k
n
k
nppp  
.
(principe de la preuve
3
: soit on avait déjà une suite de
k
résultats consécutifs identiques à l’issue du
)1( n
ième lancer, soit une telle suite apparaît au
n
ième lancer)
)1()( 
 k
n
k
nn EEPkLP
=
)(k
n
p
)1( 
k
n
p
car la suite
k
k
n
E)( )(
est décroissante pour l’inclusion.
On a représenté ci-contre chacune des suites
501
)( )(  n k
n
p
pour
k
entre 2 et 10. Bien sûr, ces suites
n
k
n
p1
)( )(
sont
(strictement) croissantes et convergent vers 1.
On peut ensuite, par soustraction de colonnes si on a un
tableur, obtenir les suites
nn kLP )( 
.
C’est fait ci-dessous pour
2001 n
avec encore
k
entre
2 et 10.
On peut noter que tous les calculs effectués sont exacts (divisions par 2).
3 ) LA VALEUR LA PLUS PROBABLE DE Ln
n
L
prend toutes les valeurs
k
entre 1 et
n
et on s’intéresse à
n
u
: Maximum sur
k
des
kLP n
, c’est
à dire : la probabilité de la plus longue suite la plus probable en effectuant
n
lancers. Cette suite
)( n u
est
représentée ci-dessous sur deux intervalles différents.
3
Cette preuve, compréhensible, en théorie, comme tout le reste de ce texte, hormis l'évocation de la formule de Stirling dans
l’introduction, par un bachelier (scientifique), comporte un passage un peu délicat, voir [1] ou [2], qui sera évoqué à la fin de ce
texte (commentaire 6) : si on la fait en terminale, par exemple pour
6k
, il faut soigneusement décomposer l’événement
« une telle suite apparaît au
n
ième lancer » en
)6(n
n
E
…0111111 et en
)6(n
n
E
…1000000 pour pouvoir utiliser
l’indépendance des six derniers lancers et de ceux qui précèdent.
0
0 ,1
0 ,2
0 ,3
0 ,4
0 ,5
0 ,6
116 31 46 61 76 91 106 121 136 151 166 181 196
N o m b r e d e l a n c e rs = n < 2 0 0
P ( L _ n = k )
k = 2
k = 3
k = 4
k = 5
k = 6
k = 7
k = 8
k = 9
k = 1 0

3
43030  n
: les quatre « arches » visibles
correspondent à
k
valant 5, 6 , 7 et 8.
Maximum sur k des P ( { L_n = k } )
0,23
0,24
0,25
0,26
0,27
Nombre de lancers = n : 30 < n < 3501
350030  n
: les quatre « arches » les plus à droite
correspondent à
k
valant 8, 9, 10 et 11.
On observe avec un tableur que l’ « arche » correspondant à « la plus longue suite la plus probable est de
longueur
k
» est obtenue, approximativement
4
, pour
n
dans l’intervalle
1
2;2 kk
.
On va montrer que contrairement à ce à ce qui se passe pour la loi binomiale évoquée dans l’introduction
et à ce que semblent indiquer les figures ci-dessus, les « arches » ne s’aplatissent pas vers 0 quand
n
grandit.
On verra plus loin que la hauteur maximum de l’arche correspondant à la valeur
k
est proche de 0,25 et
est obtenue pour
1
2.)2(  k Lnn
.
Cette étonnamment grande valeur
4
1
peut être visualisée, très informellement, sur le dessin qui suit.
k
étant un entier fixé, on désigne par N = N (
k
) le plus petit entier
n
vérifiant
2
1
)(  k
n
p
.
(cette valeur N sera précisée plus loin, c’est approximativement
k
Ln 2.)2(
).
L’arc OA représente
)(k
n
p
sur [ 0 ; N ]
)1( k
n
p
, représentée par l’arc OE, augmente deux fois moins vite, si on confond
les « décalages » de
k
pour
)(k
n
p
et
1k
pour
)1( k
n
p
, confusion d'autant
moins grave que
k
est grand, donc
)1( k
n
p
atteint
2
1
en 2.N.
L’arc AD représente
)(k
n
p
sur [ N ; 2N ]. Sur cet intervalle de longueur N,
)(k
n
p
augmente deux fois moins vite que sur l’intervalle [ 0 ; N ] car ses premiers
écarts sont
)
2
1
1(
2
1
k
environ au lieu de
)01(
2
1
k
.
)(k
n
p
monte donc de
4
1
sur cet intervalle et atteint donc
4
3
en 2.N.
On a donc bien
4
1
2
1
4
3
)1(
2
)(
2 k N
k
Npp
.
Si on saute le paragraphe suivant, dont le titre est repoussant, la preuve du paragraphe 5 est tout à
fait compréhensible mais on se demande d’où elle sort et on perd de la compréhension.
4 ) UNE METHODE MALADROITE
On va en fait prouver le résultat suivant :
4
Sur le plus grand dessin, on voit intervenir les valeurs 15, 31, 61…On va voir que « la » formule donnant les abscisses des
pieds des arches n’est pas
k
x2
mais est plutôt
)2.( k CEntx 
avec
96,0C
. Les feuilles de tableur sont sur le site
[1].

4
Pour tout
strictement positif, il existe un entier
M
tel que pour tout entier
n
vérifiant
Mn 
et pour l’entier
k
égal à
)2/)/(( LnCnLnEnt
, on a :
 kLP n
 25
.
Remarques : 1 ) On peut prouver (voir le commentaire 4) que de plus
25 
est le seul nombre vérifiant cette propriété.
2 ) On peut donner une valeur de
M
en fonction de car on montrera que est majoré par
k
k
2
.10
, par
exemple pour
3
10
, la minoration est prouvée pour
18)2/)/((  LnCnLnEntk
, c'est-à-dire si
18
2.Cn 
et on
peut prendre
1)2.( 18  CEntM
. Dans le cas contraire,
18
2n
et la vérification de la minoration peut être faite avec un
ordinateur (voir les feuilles de tableur du site [1] ).
En d’autres termes, ce résultat ne dépend d’aucun théorème asymptotique du calcul des probabilités.
La preuve du paragraphe 5 est assez simple. Les trois étapes qui suivent indiquent seulement
comment j’ai obtenu le résultat final.
Etape 1 : COMPTAGES APPROXIMATIFS DE TERMES DE
)(k
n
p
Il existe une formule exacte et explicite de la loi de
n
L
, provenant des formules de récurrence définissant les suites (
)(k
n
p
) mais
elle n’est que théorique et semble a priori inutilisable
5
à cause de la difficulté de la résolution de l’équation caractéristique
0
2
1
1 
k
kk xx
dès que
k
dépasse 5 (
2/1x
est toujours une solution) . On se contente donc de calculs approchés.
Notation :
k
étant un entier fixé valant au moins 2, pour tout
a
vérifiant
10  a
, on désigne par
)(agk
le plus petit entier
n
vérifiant
ap k
n
)(
.
Si
ap k
n
)(
,
)(agk
est le nombre de termes de (
)(k
n
p
) situés dans
a;0
.
Si
ap k
n
)(
,
)(agk
est ce nombre de termes augmenté de 1.
J’ai eu du mal à obtenir le résultat suivant :
k
étant un entier fixé valant au moins 2, pour tous entiers
A
et
s
vérifiant
k
As k
2
0
, on a
l’encadrement :
1
1
1
ln.21
2
2
ln.2 
s
sAA A
s
gs
sAAk
k
k
. (1)
Le problème était : trouver un pas trop mauvais découpage de
1;0
.
Cet encadrement est imprécis mais dans les cas qui nous intéressent il concerne des grands nombres et il va suffire ! En d’autres
termes cet encadrement de
)( A
s
gk
n’est pas excellent, surtout si
k
et
A
, donc
s
, sont grands, mais ce n’est pas gênant car il
s’agit d’un nombre situé sur l’axe des abscisses, cependant que l’ordre de grandeur des écarts sur l’axe des ordonnées est
k
2
1
.
Etape 2 : UNE FORMULE D’APPROXIMATION DE
)(k
n
p
En prenant la demi-somme des bornes de (1) et en la simplifiant un peu, on obtient une valeur approchée
de
A
s
gk
:
sA
A
A
s
gk
kln.2
. On peut en déduire une expression approchée de
n
p
:
5
Elle est évoquée au commentaire 5.

5
pour
A
s
sAA
nkk
1
1
ln.2ln.2
, alors
A
s
pk
n
)(
, c’est à dire que
)
2
(exp
11)( kk
n
n
p
,
soit :
k
n
k
nep 2
)( 1
. (2)
On peut tester informatiquement cette approximation pour les petites valeurs de
k
( voir les dessins ci-dessous pour
k
valant
3,4,5 puis 11 ,12 et 13), elle semble très convenable (et on peut vérifier, informellement, que la suite
n
n
k
e)1( 2
vérifie
approximativement la relation de récurrence définissant
n
k
n
p)( )(
).
Ainsi, en considérant
k
c
définie par
k
x
kexc 2
1: 
,
)(nck
est une bonne approximation de
)(k
n
p
.
De même, avec
)()(: 1xcxcxd kkk 
,
)(ndk
=
kk nn ee 22 1 
est une (bonne) approximation de
)(k
n
p
)1( 
k
n
p
=
.kLP n
Ce sont ces fonctions
k
c
et
k
d
qui sont utilisées dans tous les dessins qui suivent.
Etape 3 : CONSEQUENCES DE CETTE FORMULE D’APPROXIMATION
On peut résoudre, pour tout
k
, l’équation, d’inconnue
x
,
)()( 1xdxd kk 
, c'est-à-dire avoir une valeur
approchée des abscisses des « pieds des arches ».
En posant
1
2
k
n
eX
, on obtient l’équation
01
2 XX
puis :
 1 2.
215 k
kLnxx
kkk CLn 2.962,02.2.
15
21
.