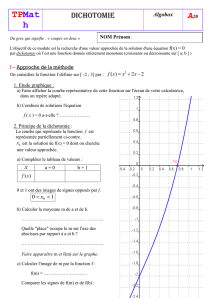
2nde TP05 : Nombre d`or et dichotomie Algobox

2nde
TP05 : N et dichotomie
Algobox
On rappelle une définition travaux de Vitruve ,
architecte romain au 1er siècle avant notre ère.
Sur un segment , est placé un point C délimitant deux segments  et
. déterminé par une proportion :
« Il y a de la petite partie à la grande, le même rapport que de la grande au tout 
I. 
Dans le DM 10 nous avons prouver que le nombre d'or est la solution positive de l'équation
      . De plus à l'aide de la calculatrice nous avons réussi à trouver que ce nombre était
compris entre 1 et 2. Nous allons essayer d'affiner cet encadrement.
1. Principe de dichotomie
intervalle  en partant des valeurs 1 et 2.
On crée les 2 variables a et b de type nombre
et on utilise une fonction numérique pour
    .
Pour commencer l'algorithme :
On sélectionne la ligne puis
Pour affecter une valeur à une variable :
puis
Créer la boucle "Tant que"
puis
Créer une condition "Si"
Ne pas oublier de cocher
Pour afficher les variables
Remarque : pour écrire une puissance, exemple :
pow(10,-4) donne 
II. Détermination de la valeur exacte de de façon algébrique
2. Montrer que   
     .
3. En déduire une factorisation de      et donc que   
.
L     , noté   
 .
On repère (en général graphiquement) un intervalle  qui contient , assez petit pour ne pas
, puis recommencer avec le
enir un encadrement de  avec la précision voulue.
Variables : a, b, deux nombres réels.
Début
Définir F1
a prend la valeur 1.
b prend la valeur 2.
Tant que     
Si  
Alors 
.
Sinon 
.
Fin Si
Fin Tant que
Afficher a, b.
Fin