integrales

Formulaire
Intégrales
4eEco
1) Définition
fétant une fonction continue sur un intervalle I.
On appelle intégrale de fentre aet b, le réel noté ( )
b
af x dx
défini par : ( ) [ ( )] ( ) ( )
bb
a
af x dx F x F b F a  
2) Propriétés
( ) 0
a
af x dx
( ) ( )
b a
a b
f x dx f x dx 
( ) ( ) ( )
c b c
a a b
f x dx f x dx f x dx 
   (Relation de Chasles)
[ ( ) ( )] ( ) ( )
c b c
a a b
f x g x dx f x dx g x dx
   (Linéarité de l’intégrale)
3) Intégration par parties
u et v étant deux fonctions dérivables sur un intervalle I, et a, b deux éléments de I
on a : ( ). '( ) [ ( ) ( )] '( ). ( )
b b
b
a
a a
u x v x dx u x v x u x v x dx 
4) Positivité
Si a<bet si f(x) ≥ 0 pour tout x[a,b] alors ( )
b
af x dx
 ≥ 0.
Si a<bet si f(x) ≥g(x) pour tout x[a,b] alors ( ) ( )
b b
a a
f x dx g x dx
5) Valeur moyenne
f étant une fonction définie et continue sur un intervalle I, a et b deux réels distincts de I, on
appelle valeur moyenne de f sur [a,b] et on notre fle réel :
1 ( ) ( )
( )
b
a
F b F a
f f t dt
b a b a
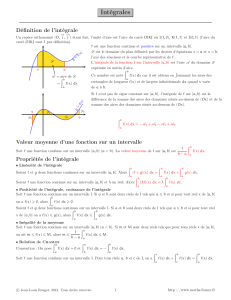
6)Calculd’aires
Théorème
fétant une fonction continue sur un intervalle
[a,b] (a< b) , et le plan étant rapporté à un repère
orthonormé alors l’aire de la partie du plan limitée par
les droites d’équations x=aet y=b, l’axe des
abscisses et la courbe représentative de fa pour mesure A=( )
b
af x dx
En particulier
Si fest positive sur [a,b] (a < b), alors A=( )
b
af x dx
Si fest négative sur [a,b] (a < b), alors A=( )
b
af x dx
Théorème
Si f ≤ g , alors A=( ) ( )
b
ag x f x dx
(f > 0)
( f < 0)
f g
<