I. Continuité II. Propriétés des valeurs intermédiaires

Lycée Jules Verne 2016-2017
TES
Continuité A. Heliard
I. Continuité
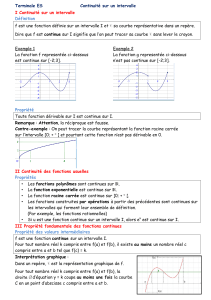
Une fonction fest continue sur un intervalle Isi on peut la représenter "sans lever le crayon". Autrement dit, la
représentation graphique de fest en un seul morceau sur l’intervalle.
1
2
3
−1
−2
−3
1 2 3 4−1−2
fn’est pas continue
1
2
3
−1
−2
−3
1234−1−2
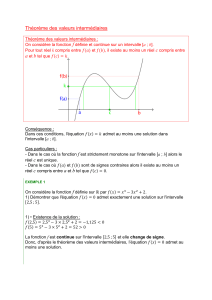
fest continue
Définition(s).
1. Les fonctions polynômiales, en particulier, affine, du second degré et cube, sont continues sur R.
2. La fonction inverse est continue sur ]− ∞; 0[ et sur ]0; +∞[.
3. La fonction racine carrée est continue sur [0; +∞[.
Proposition.
Toute fonction dérivable sur un intervalle est continue sur cet intervalle.
Proposition.
☞ex 15, 16 p 62, ex 24 p 62
II. Propriétés des valeurs intermédiaires
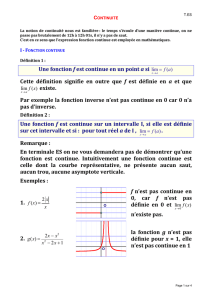
Soit fune fonction continue sur un intervalle [a;b].
Pour tout réel kcompris entre f(a)et f(b), l’équation f(x) = kadmet au moins une solution dans l’intervalle [a;b].
Théorème.
1

Lycée Jules Verne 2016-2017
TES
Continuité A. Heliard
•Si fest continue et strictement monotone sur un intervalle [a;b], alors pour tout réel kcompris entre f(a)et
f(b), l’équation f(x) = kadmet une unique solution dans l’intervalle [a;b].
•En particulier, si fest continue, strictement monotone sur un intervalle [a;b]et si f(a)et f(b)sont de signes
contraires, alors l’équation f(x) = 0 admet une unique solution dans l’intervalle [a;b].
Corollaire.
Soit fla fonction définie sur [−1; 3] par f(x) = x3−9
2x2+ 6x−5 4.
1. Dresser le tableau de variations de f.
2. Déterminer le nombre de solutions de l’équation f(x) = 1.
3. Déterminer le nombre de solutions de l’équation f(x) = 0.
4. En déduire le tableau de signes de f.
Exercice (Exercice - type ❤).
☞ex p 58 (oral)
☞ex 32 p 63, ex 41, 42 à 45, 47 p 65
☞ex 49, (50) p66, ex 63 p 71
2