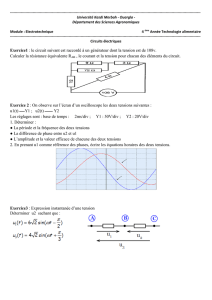
Annexe A Formules

Z+∞
−∞
exp −X2dX =√π
I=R+∞
−∞ e−x2dx
I2=Z+∞
−∞
e−x2dxZ+∞
−∞
e−y2dy=Z+∞
−∞ Z+∞ −∞
e−(x2+y2)dxdy
=Z∞
0
drr Z2π
0
dθe−r2= 2πZ∞
0
re−r2dr = 2π−1
2e−r2∞
0=π
I=√π
Q(x) = Ax2+Bx +C
A, B, C ∈C<(A)>0.
Z+∞
−∞
exp (−Q(x)) dx =rπ
Aexp −C+B2 4A

n≥0
Z+∞
−∞
x2ne−x2dx =√π(2n−1)!!
2n
(2n−1)!! := (2n−1) (2n−3) . . . 5.3.1 == (2n)!
2n(n!)
R+∞
−∞ x2n+1e−αx2dx =
0
R+∞
−∞ e−αx2dx α α = 1
Iα:= Z+∞
−∞
e−αx2dx =rπ
α
dnIα
dαn=Z+∞
−∞ −x2ne−αx2dx =√π−1
2−3 2. . . −2n−1 2
Z+∞
−∞
x2ne−αx2dx =√π(2n−1)!!
2n
R3
hx|1
−∆ + k2|yi=eik|x−y| 4π|x−y|
k=iκ ∈iR
~= 1
hx|1
−∆ + k2|yi=Zd3~phx|pihp|yi1 (p2+κ2)
=1
(2π)3Zd3~pei~p.(x−y)1
(p2+κ2)
hx|1
−∆ + k2|yi=e−κ|x−y| 4π|x−y|=eik|x−y| 4π|x−y|

2×2
A=a b
c d 
∆ = (a−d)2+ 4bc.
∆6= 0 A
A=P DP −1, P =a−d+√∆a−d−√∆
2c2c, D = a+d+√∆
20
0a+d−√∆
2!,
P
A=0b
b0, P =|b| −|b| b b , D =|b|0
0−|b|
[ˆq, ˆp] = i~
[ˆq, F (ˆp)] = i~dF (ˆp)
dˆp
[F(ˆq),ˆp] = i~dF (ˆp)
dˆq

A, B
[A, [A, B]] = [B, [A, B]] = 0
exp (A) exp (B) = exp ([A, B]/2) exp (A+B)
C=i[A, B] (A, B, C)
ˆq, ˆp, i~
C= [A, B],[A, C] = [B, C]=0
a=
0 1 0
0 0 0
0 0 0 
, b =
000
001
000
, c =
001
000
000
3×3eaeb=ec/2ea+b
~σ. ~
A~σ. ~ B=~ A. ~ B+i~σ. ~ A∧~ B
~
A, ~ B
~u
exp (iϕ~σ.~u) = cos ϕ+isin ϕ ~σ.~u
A
eA=e(A)
2×2
A=a b
c d (A) = ad −bc 6= 0
A−1=1
(A)d−b
−c a 

R3
A, B, C
[AB, C] = A[B, C]+[A, C]B
[AB, C] = ABC −CAB =A([B, C] + CB)−CAB
=A[B, C]+[A, C]B
R3
f(~x)~ V(~x)
◦V(x, y, z)~ W=−−→V
Wx=∂V
∂x , Wy=∂V ∂y , Wz=∂V ∂z −−→V=~
∇V
◦~ E= (Ex, Ey, Ez)~ E(~x)
~
W=−→~ E
Wx=∂Ez
∂y −∂Ey ∂z
Wy=∂Ex
∂z −∂Ez ∂x
Wz=∂Ey
∂x −∂Ex ∂y
−→~
E=~ ∇ ∧ ~ E~ ∇=
∂
∂x ,∂ ∂y ,∂ ∂z 
◦~
E=∂Ex
∂x +∂Ey ∂y +∂Ez ∂z 
~
E=~ ∇.~ E
◦∆V
∆V=∂2V
∂x2+∂2V ∂y2+∂2V ∂z2