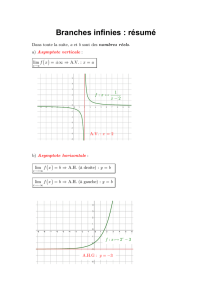
Branches infinies

Branches infinies : résumé
Dans toute la suite, a et b sont des nombres réels.
a) Asymptote verticale :
lim A.V. :
xa
fx x a
b) Asymptote horizontale :
lim A.H. (à droite) :
x
fx b y b
lim A.H. (à gauche) :
xfx b y b

Lorsque
lim
xfx
, il y a 4 possibilités (en pratique …)
c1) Asymptote oblique :
lim et l0im A.O. :
xx
fx f x ax b y aaxb
x
c2) Branche parabolique de direction asymptotique
()Ox
lim et lim B.P. de directio )
0n (
xx
fx
f x Ox
x
(Lorsque
x 
,
()fx 
, mais
()
fx
est négligeable, c.-à-d. petit par
rapport à x.)

c3) Branche parabolique de direction asymptotique
()
Oy
lim et
lim B.P. de direction ( )
x
x
fx
fx Oy
x
(Lorsque
x 
,
()fx 
, et
()
fx
est grand par rapport à x.)
c4) Branche parabolique de direction asymptotique
y ax
0 li
lim et
lim et B.P. de Dm () .A.
x
x
xa f x ax
fx
fx y ax
x
(Lorsque
x 
, le rapport ()fx a
x
, mais la différence
()f x ax
,
c.-à-d. le graphe de f s’éloigne de plus en plus de la droite
y ax
.)

Exercices
Etudier l’existence et la nature des branches infines des graphes des fonctions
suivantes :
1)
3
:fx x
2)
:2 3
f x xx
3)
32
:1
xx
fx x
4)
: 12 1fx x x 
5)
2
1
:1
x xx
fx x