Approximation affine associé à une fonction

Approximation affine associé à une fonction
1) Propriété-définition :
f est une fonction définie sur un intervalle I et a est un réel de I. Si f est dérivable en a, alors il existe une fonction  telle
que pour tout réel h, avec a + h dans I : f(a + h) = f(a) + h f’(a) + h (h) et (h) = 0.
On dit que f(a) + h f’(a) est l’approximation affine de f(a + h) pour h proche de 0, associée à f.
Démonstration :
Pour h  0, on pose (h) = – f’(a). Or f est dérivable en a donc lorsque h tend vers 0, (h) tend vers
f’(a) – f’(a) c’est-à-dire 0. D’autre part, h (h) = f(a + h) – f(a) – h f’(a), soit :
f(a + h) = f(a) + h f’(a) + h (h) (égalité vraie aussi pour h = 0).
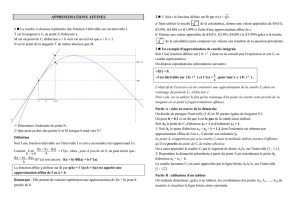
2) Interprétation graphique : lien avec la tangente
Cf est la courbe de f et (T) est la tangente à Cf au point A d’abscisse a.
Si on pose h = x – a dans la définition ci-dessus, on obtient :
f(a) + (x – a) f’(a) comme approximation affine de f(x) pour x proche de a.
Or la tangente (T) en A(a ; f(a)) a pour équation : y = f’(a) (x – a) + f(a)
La tangente en A est la meilleure façon d’approcher la courbe au voisinage
de A à l’aide d’une droite.
MN = = .
Lorsque h tend vers 0, tend vers 0.
Donc f(a) + h f’(a) est une valeur approchée de f(a + h) d’autant meilleure que h est proche de 0.
3) Exemple d’approximation de courbe intégrale : Méthode d’Euler
On appelle courbe intégrale d'une fonction dérivable la courbe représentative d'une fonction f dont on connaît seulement
un point particulier ainsi que l'expression de f '(x).
Le plan est muni d'un repère orthogonal ( O ;,)
(unités : 5 cm sur l'axe des abscisses et 10 cm sur l'axe des ordonnées)
Soit f une fonction définie sur [1 ; 2] dont on ne connaît pas l'expression et soit Cf sa courbe représentative.
On dispose cependant des informations suivantes :
 f(1) = 0,
 f est dérivable sur [1 ; 2] et f '(x) = – x + 3 , pour tout x  [1 ; 2].
L'objectif est de construire une approximation de la courbe Cf dans un voisinage du point de Cf d'abscisse 1.
Pour cela, on va utiliser le fait qu'au voisinage d'un point, la courbe reste proche de sa tangente en ce point.Suite de
l’exemple d’approximation de courbe intégrale : Méthode d’Euler
Partie A

Soit A0 le point de Cf d'abscisse 1.
1/ Déterminer une équation de la tangente T0 à Cf en ce point.
2/ Soit B0 le point de T0 d'abscisse 1,2. Calculer ses coordonnées puis construire le segment [A0B0].
On a ainsi approché la courbe Cf par un segment de droite sur l'intervalle [1 ; 1,2]
Partie B
Soit A1 le point de la courbe Cf qui a pour abscisse 1,2.
On ne sait pas calculer son ordonnée car on ne connaît pas l'expression de f(x) mais on peut penser qu'il est voisin du
point B0 défini précédemment. On décide alors d'approcher la courbe Cf sur l'intervalle [1,2 ; 1,4] par la droite T1 passant
par B0 et de coefficient directeur f '(1,2).
1/ Déterminer une équation de la droite T1.
2/ Soit B1 le point de T1 d'abscisse 1,4. Calculer ses coordonnées puis construire le segment [B0B1].
La courbe inconnue Cf est ainsi approchée par la ligne brisée A0B0B1 sur l'intervalle [1 ; 1,4]
Partie C
Réitérer le procédé de construction décrit précédemment et construire la ligne brisée A0B0B1B2B3B4 sur l'intervalle [1 ; 2]
où B2, B3 et B4 ont pour abscisses respectives 1,6 , 1,8 et 2.
Partie D
On donne la fonction f définie sur [1 ; 2] par f(x) = – + 3x –
1/ Vérifier que f correspond aux hypothèses initiales.
2/ À l'aide de la calculatrice (graphique et tableau de valeurs), tracer dans le même repère que précédemment la courbe
représentative de la fonction f dans l'intervalle [1 ; 2]
3/ On admettra que la fonction f ainsi définie est la fonction dont on a cherché à approcher la courbe représentative.
L'approximation obtenue dans la partie C est-elle de bonne qualité ? Comment aurait-on pu améliorer le résultat ?
Partie E (en salle informatique) : utilisation d’un tableur
Nous allons reprendre le même problème en utilisant un logiciel de type tableur qui permettra d’améliorer
l’approximation de la courbe obtenue précédemment.
On utilisera l’approximation affine : f(1 + h)  f(1) + h f’(1) (où h représente le pas) pour calculer les ordonnées yi des
points qui approchent la courbe.
1/ Préparer la feuille de calculs comme ci-contre.
2/ Dans la cellule A5, taper la formule =A4+$B$1
Puis en maintenant cliqué sur la poignée de recopie (petit carré en bas à
droite de la cellule) tirer vers le bas jusqu’à la cellule A14.
3/ Dans la cellule B5, taper la formule =B4+$B$1*(-A4+3)
Recopier ensuite vers le bas la formule jusqu’en B14.
4/ Dans la cellule C4, taper la formule qui permet de calculer la valeur
réelle de f(1) (voir partie D) puis recopier cette formule jusqu’en C14.
5/ Pour tracer la courbe et son approximation, sélectionner toutes les valeurs (de la cellule A4 à la cellule C14) puis Menu
« insérer »  diagramme  première colonne comme étiquette  suivant  1ier graphe (lignes)  suivant  1ier
graphe (normal)  suivant  « décocher » titre et légende  créer.
6/ Après observation, modifier le pas (0,05 par exemple) sans oublier de recopier les formules jusqu’à xi = 2 puis créer un
nouveau graphe. Que constate-t-on ?
A
B
C
1
pas
0,1
2
3
xi
yi
f(x)
4
1
0
5
6