fonction reciproque

Définition
f étant une application d’un ensemble E dans un ensemble F.
On dit que : f réalise une bijection de E sur F
si et seulement si
yF ;il existe un seul x E tel que y fx
VOCABULAIRE:
Soit f une bijection de I sur J. On note f
1
la bijection réciproque de f.
Ainsi: f
1
: J I.
yJ ; ff
1
y y
xI ; f
1
fx x.
Théorème
f étant une fonction définie sur un intervalle I.
si f est strictement monotone sur I alors f réalise une bijection
de I sur f(I).
Remarque importante
f est une bijection de I sur fIJ
0JfI
0 possède un seul antécédent par f dans I
l’équation f(x)0 admet une seule solution dans I.
Remarques
O; i ; j est un repère orthonormé du plan P. S
la symétrie axiale
d’axe :y x. On a:
S
M a, b M
b, a .
L’image d’une droite D : y a (a IRpar S
est la droite D’: x a
Hadj Salem Habib
Lycée pilote Médenine
Fonction réciproque
Théo rème
Soit f une fonction strictement monotone sur un intervalle I.
Désignons par f
1
la bijection réciproque de f et par J fI.
On a:
1f
1
et f ont même sens de variation.
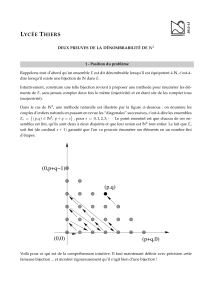
2les courbes de f et de f
1
, dans un repère orthonormé, sont symétriques
par rapport à la droite d’équation y x dite la première bissectrice.
3si f est continue sur I alors f
1
est aussi continue sur J f(I).
Hadj Salem Habib
Lycée pilote Médenine
Bac Maths Bac Sc exp
( 1 )

0 1 2
3
4
1
2
3
-1
-1
x
y
C
f
C
f
1
Théo rème
f est une bijection d’un intervalle I sur un intervalle J. Soit x
0
I et
y
0
fx
0
. On a:
si f est dérivable en x
0
et f
x
0
0alors f
1
est dérivable en
fx
0
y
0
de plus f
1
y
0
1
f
x
0
1
f
f
1
y
0
.
si f est dérivable sur I
0
Iet f
x0 ;xI
0
alors f
1
est
dérivable sur fI
0
J
0
et de plus xJ
0
; f
1
x
1
f
f
1
x.
Théorème
Définition
Soit n un entier supérieur ou égal à 2. La fonction xx
n
réalise
une bijection de IR
sur IR
. La bijection réciproque de xx
n
est
la fonction dite racine nième et elle est notée x
n
x.
Pour tous réels positifs x et y on a : y x
n
x
n
y
Soient deux entiers n et p tels que n 2 et p 2 et deux positifs a et
b. Alors :
n
a
n
a;
n
a
n
a;
n
a.b
n
a
n
b;
n
a
b
n
a
n
bavec b 0.
n
a
np
a
p
;
n
a
p
n
a
p
;
np
a
np
a.
3. Fonction racine nième
Propriétés
Théorème
Soient n IN
\1et u une fonction dérivable et strictement positive
sur un intervalle I. On a:
1/ La fonction x
n
xest continue sur 0;et dérivable sur 0;de plus
n
x
1
n
n
x
n1
;x0.
2/ La fonction x
n
uxest dérivable sur I et que
n
x
u
x
n
n
ux
n1
;x0.
Hadj Salem Habib
Lycée pilote Médenine
Fonction réciproque
Hadj Salem Habib
Lycée pilote Médenine
Bac Maths Bac Sc exp
( 2 )
1
/
2
100%