p,q - MPSI-3

LYCÉE THIERS
DEUX PREUVES DE LA DÉNOMBRABILITÉ DE N2
1 - Position du problème
Rappelons tout d’abord qu’un ensemble Eest dit dénombrable lorsqu’il est équipotent à N, c’est-à-
dire lorsqu’il existe une bijection de Ndans E.
Intuitivement, construire une telle bijection revient à proposer une méthode pour énumérer les élé-
ments de E, sans jamais compter deux fois le même (injectivité) et en étant sûr de les compter tous
(surjectivité).
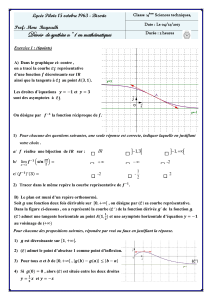
Dans le cas de N2, une méthode naturelle est illustrée par la figure ci-dessous : on énumère les
couples d’entiers naturels en passant en revue les “diagonales” successives, c’est-à-dire les ensembles
Es=(p,q)∈N2;p+q=s, pour s=0, 1, 2, 3, ··· Le point essentiel est que chacun de ces en-
sembles est fini, qu’ils sont deux à deux disjoints et que leur union est N2tout entier. Le fait que Es
soit fini (de cardinal s+1)garantit que l’on va pouvoir énumérer ses éléments en un nombre fini
d’étapes.
(0,p+q−1)
(0,0) (p+q,0)
(p,q)
Voilà pour ce qui est de la compréhension intuitive. Il faut maintenant définir avec précision cette
fameuse bijection ... et montrer rigoureusement qu’il s’agit bien d’une bijection !

DEUX PREUVES DE LA DÉNOMBRABILITÉ DE N22
2 - Définition de f
Soit (p,q)∈N2. Les couples qui précèdent celui-ci dans l’énumération décrite ci-dessus sont les
suivants :
(0, 0)Total : 1
(1, 0);(0, 1)Total : 2
(2, 0);(1, 1);(0, 2)Total : 3
... etc ...
(p+q−1, 0);(p+q−2, 1);···;(1, p+q−2);(0, p+q−1)Total : p+q
et encore :
(p+q, 0);(p+q−1, 1);···;(p+1, q−1)Total : q
On considère donc l’application :
f:N2→N,(p,q)7→ [1+2+··· +(p+q)] +q=(p+q) (p+q+1)
2+q
et l’on montre qu’il s’agit d’une bijection.
3 - fest surjective
Soit n∈N. Considérons l’entier :
N=max k∈N;k(k+1)
26n
Nest bien défini car la suite k(k+1)
2k∈Ndiverge vers +∞. La définition de Ndonne l’encadrement :
N(N+1)
26n<(N+1) (N+2) 2(1)
Posons alors :
q=n−N(N+1)
2;p=N−q
Il est clair que q>0. De plus :
p=N−n−N(N+1)
2=N2+3N 2−n=(N+1) (N+2) 2−n−1>0
Ainsi (p,q)∈N2et f(p,q)=n. La surjectivité de fest établie.
4 - fest injective
Soient (p,q)∈N2et (p0,q0)∈N2tels que f(p,q)=f(p0,q0).
Posons N=p+q; alors :
N(N+1)
26N(N+1) 2+q=f(p,q)<(N+1) (N+2) 2
la dernière inégalité résultant de :
(N+1) (N+2)
2−f(p,q)=N+1−q=p+1>0

DEUX PREUVES DE LA DÉNOMBRABILITÉ DE N23
Donc :
p+q=max k∈N;k(k+1)
26f(p,q)
Il en résulte dans un premier temps que p+q=p0+q0, puis :
q=f(p,q)−(p+q) (p+q+1)
2=fp0,q0−(p0+q0) (p0+q0+1) 2=q0
et finalement (p,q)=(p0,q0).
5 - Et la bijection réciproque ?
Reprenons le calcul de la section 3. Il est possible d’expliciter Nen fonction de n. En effet, l’application
R→R,t7→ t(t+1)
2induit une bijection croissante ϕde [0, +∞[dans lui-même, dont la bijection
réciproque est :
ϕ−1:[0, +∞[→[0, +∞[,x7→ 1
2−1+√1+8x
On constate alors, en appliquant ϕ−1à chaque membre de (1), que :
N61
2−1+√1+8n<N+1
d’où (en notant bxcla partie entière du réel x):N=1
2−1+√1+8n. Notons N(n)cet entier
(changement de notation ! Nest devenu une application ...). Alors la bijection réciproque de fest :
f−1:N→N2,n7→ N(n)−n+1
2N(n) (N(n)+1),n−1 2N(n) (N(n)+1)(2)
Voici ce que cela donne en Maple :
N:=n→floor((-1 + sqrt(1+8*n))/2);
recip:=proc(n)
local m,r;
m:=N(n);
r:=m*(m+1)/2;
[m-n+r, n-r]
end proc;
En anglais, floor désigne le plancher, le sol. Pour Maple (et pour d’autres langages informatiques),
c’est le nom de la fonction “partie entière”.
Question : pourquoi avoir utilisé des variables locales et ne pas avoir écrit d’un coup l’expression
correspondant à (2) ? Réponse : ici 1.
6 - Une autre bijection de N2dans N
Il est bien connu que tout entier naturel n>2 est produit de nombres premiers. Il s’ensuit que :
∀n∈N?,∃(p,q)∈N2;n=2p(2q+1)
car les nombres premiers autres que 2 sont tous impairs et un produit d’entiers impairs est impair!
1. Simplement pour ne pas recalculer 5 fois la même expression.

DEUX PREUVES DE LA DÉNOMBRABILITÉ DE N24
Autrement dit, l’application :
g:N2→N?,(p,q)7→ 2p(2q+1)
est surjective.
Elle est aussi injective, car si (p,q)∈N2et (p0,q0)∈N2vérifient :
2p(2q+1)=2p02q0+1
et si (par exemple) p<p0, alors 2q+1=2p0−p(2q0+1), égalité entre deux entiers de parités dis-
tinctes ! Donc p=p0nécessairement, et du coup q=q0.
Finalement, gest une bijection.
Comme N?est équipotent à N(via la bijection N?→N,n7→ n−1), on retrouve le fait que N2est
dénombrable en composant deux bijections.