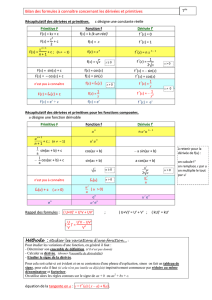
Chapitre 1

IRf, F :−→ RF
f F t ∈I F 0(t) = f(t)
IRf:I−→ Rf
F I
IRf:I−→ RF1F2f
F1F2C∈RF1(t) = F2(t)+C
t∈I
f I f
Zf(t)dt.
R
f g I
λ∈R
Z(f(t) + g(t))dt =Zf(t)dt +Zg(t)dt, Zλf(t)dt =λZf(t)dt.
Ztet2dt =Z2
2tet2dt =1 2Z2tet2dt =1 2et2.
IRf:I−→ Ra, b I
f a b
Zb
a
f(t)dt =F(b)−F(a),
F f I
fRb
af(t)dt
F f Rb
af(t)dt
{(x, y)∈R2|a≤x≤b, 0≤y≤f(x)}.

f, g :I−→ R
f g C1
Zf(t)g0(t)dt =fg −Zf0(t)g(t)dt.
F fg0G fg0F+G
f0g+fg0= (f g)0fg
Rf(t)g0(t)dt +Rf0(t)g(t)dt =fg 2
f, g :I−→ R
C1a, b I
Zb
a
f(t)g0(t)dt = [fg]b
a−Zb
a
f0(t)g(t)dt,
[h]b
a=h(b)−h(a)h[a, b]
Zte2tdt =te2t
2−Ze2t 2dt =te2t 2−1 2Ze2tdt =te2t 2−1 2
e2t
2=te2t 2−e2t 4.
f=t g0=e2tf0= 1 g=e2t
2
Rtneαtdt n ≥1n
Zπ
0
t2cos(t)dt = [t2sin(t)]π
0−2Zπ
0
tsin(t)dt
= 0 −2[tcos(t)]π
0−2Zπ
0
cos(t)dt
=−2π−2[sin(t)]π
0
=−2π.
f=t2
g0= cos(t)f0= 2t g = sin(t)f=t g0= sin(t)f0= 1
g=−cos(t)−
Zln(t)dt =tln(t)−Zt
tdt =tln(t)−Zdt =tln(t)−t.
f= ln(t)g0= 1 f0=1
tg=t
f:I−→ Rφ:J−→ RC1φ(J)⊆I
a, b J
Zb
a
f(φ(t))φ0(t)dt =Zφ(b)
φ(a)
f(t)dt.

F f F ◦φ J
t∈J
(F◦φ)0(t) = F0(φ(t))φ0(t).
Zb
a
f(φ(t))φ0(t)dt =F(φ(b)) −F(φ(a)) = Zφ(b)
φ(a)
f(t)dt.
2
Z√2π
√π
2tcos(t2)dt =Z2π
π
cos(t)dt = [sin(t)]2π
π= 0.
φ(t) = t2x=t2dx = 2tdt
Z√2π
√π
2tcos(t2)dt =Z2π
π
cos(x)dt.
Z
π
2
0
sin(t)ecos(t)dt =−Z0
1
exdx =Z1
0
exdx = [ex]1
0=e−1.
x= cos(t)dx =−sin(t)dt