Méthodes de probabilité : Guide de maths ECE 2

•
B
An+1 Xn+1
n n + 1
•
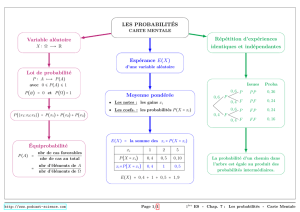
P((X=k)∩(Y=l)) P(X=k)(Y=l)
P(Y=l)
Z=f(X, Y )P(X+Y=k)P(XY =k)...
P(X1=X2)P(X1< X2)

P(X > k)
(X6k)k(X > k)
P(X > k) = 1 −P(X6k)
Y
Y=f(X)
P(f(X) = k)f(X) = k X
X=g(k)
P(f(X)6x)
(X, Y )P((X=i)∩(Y=j))
Y X PX=i(Y=j)
PB(A)PX=i(Y=j)
X
P((X=i)∩(Y=j))
A⊂B P (A∩B) = P(A)P(A∩B) = P(B\A) = P(B)−P(A)
X Y
Y=f(X) (X=i)∩(Y=j)
X
Y X
(X=i)∩(Y=j)

E(Y)
Y
Y
Y=f(X)X
V(Y)
Y Y =aX V (aX) = a2V(X)
Y Y =X+a V (X+a) = V(X)
Y V (PXk) = PV(Xk)X=Y+Z
V(X+Z) = V(X) + V(Z) + 2cov(X, Z)
X Y E(XY )
XY Cov(X, Y ) = E(XY )−E(X)E(Y)
cov(X, Y ) = 1
2(V(X+Y)−V(X)−V(Y))
X Y X +Y
1
/
3
100%