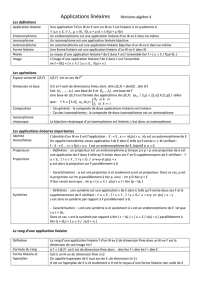
COURS PCSI R. FERREOL 04/05 B) APPLICATIONS LINÉAIRES

COURSPCSI 10.ALGÈBRELINÉAIRE:APPLICATIONSLINÉAIRES R.FERREOL04/05
B)APPLICATIONSLINÉAIRES
REM:danscecours, ,et désignentdes -espacesvectoriels.
I)GÉNÉRALITÉS.
1)Dé…nition.
DEF:Soit uneapplicationde dans ;onditque est -linéaire (ouquec’estun morphisme de -espaces
vectoriels)si estunmorphismepourlesdeuxloisdé…niessur et  c’est-à-diresi
1. 8¡! ¡! 2(
¡!
+
¡!
)=(
¡!
)+(
¡!
)
2. 8¡! 282(
¡!
)= (¡! )
REM1:onpeutregrouper1.et2.enunseulénoncé:
38
¡!
¡! 282(
¡!
+
¡!
)=(
¡!
)+ (¡! )
D1
REM2:1.signi…eque estunmorphismedugroupe ( +) verslegroupe ( +) :maiscecinesu¢tpaspourque 
soitlinéaire;parexemple, 7! estunmorphismeadditifde Cdans C,maisellen’estpas C-linéaire(parcontre,elleest
R-linéaire).
Premièrespropriétés:si estlinéaire:
³¡! 0
´=¡!
0
Ã
X
=1
¡! !=
X
=1
(¡! )(donc ( (¡! ))=((¡! )))
D2
2)Exemples.
)Homothétiesvectorielles.
DEF:pourtoutscalaire ettout ¡! de  onpose (¡! )=
¡!
;l’application 2estappeléel’homothétie
(vectorielle)derapport 
PROP:leshomothétiessontlinéaires.
D3
Propriétésimmédiates:
1= =
±= =±
estbijectivessi 6=0et ()¡1=1
L’ensemble ()deshomothétiesvectoriellesde derapportnonnul
estunsous-groupede ( ()±)isomorpheà(
¤
£)si n’estpsréduitàf
¡!
0g
D4
PROP:si estunedroite(doncparexemplesi =)leshomothétiessontlesseulesapplicationslinéairesde dans
D5
)Projectionsvectorielles.
Ellesontétédé…niesaumomentdessommesdirectes.
PROP:lesprojectionssontlinéaires.
D6
1
PDF created with pdfFactory trial version www.pdffactory.com

COURSPCSI 10.ALGÈBRELINÉAIRE:APPLICATIONSLINÉAIRES R.FERREOL04/05
Propriétésimmédiates:si =©,soient (resp )laprojectiondebase (resp )etdedirection (resp ):
8
¡!
¡! 02¡! 0=(
¡!
),½¡!
02
¡!
0¡¡! 2
±=±=
0
+=
1
=
si ==
1=
si ==
0
D7
)Exemplesde 2dans 2
E1
)Exemplesenanalyse.
E2:limite,dérivée,intégrale.
3)Vocabulaire.
Uneapplicationlinéairede danslui-mêmeestappeléeun endomorphisme de 
Uneapplicationlinéairebijectiveestappeléeun isomorphisme d’espacesvectoriels.
Unendomorphismede bijectifestappeléun automorphisme de 
E3
II)ESPACEVECTORIELDESAPPLICATIONSLINÉAIRES ()
Notation:()estl’ensembledesapplicationslinéairesde dans :
()=f2 estlinéaire}
Quand = onabrègelanotationen ()(ou ())
PROP:()estunsous-espacevectorielde 
D8
Parexemple,sicommeci-dessus et sontlesdeuxprojectionsassociéesàladécomposition =© alorspourtous
scalaires  + estlinéaire.Cecidonnedenouveauxexemplesd’endomorphismesde ;enparticulier:
DEF:l’application =¡estappeléela symétrie(vectorielle) de base etde direction (ou symétrieparrapport
àet parallèlement à)
Propriétésimmédiates:
8
¡!
¡! 02¡! 0=(
¡!
),½¡!
+¡! 02
¡!
0¡¡! 2
=2¡±=
1
=(onditque est involutive)
si ==
1=
si ==
¡1=¡
D9
Etplusgénéralement:
DEF:l’application =+ estappeléela dilatation (ou a¢nité)(vectorielle) de base ,de direction etderapport
REM:quand =0onretrouveles................,quand =¡1onretrouveles............,etpour =1l’............
III)COMPOSITIONDESAPPLICATIONSLINÉAIRES
2
PDF created with pdfFactory trial version www.pdffactory.com

COURSPCSI 10.ALGÈBRELINÉAIRE:APPLICATIONSLINÉAIRES R.FERREOL04/05
PROP:lacomposéededeuxapplicationslinéairesestlinéaire;plusprécisément:
si 2()et 2()alors ±2()
D10
Lacompositiondesapplicationdé…nitdoncuneloidecompositioninternedans ();onaalorslastructureremarquable
:
PROP:(()+±)estunanneau,quiestnoncommutatifetnonintègredèsque dim >2
D11
Exempled’application:aveclanotationdesa¢nitésci-dessus:
± =
IV)NOYAUETIMAGED’UNEAPPLICATIONLINÉAIRE.
1)Noyau.
a)Dé…nitionetpremièrespropriétés.
DEF:lenoyaud’uneapplicationlinéaireestl’ensembledesvecteursdel’ensemblededépartquiontpourimagelevecteur
nuldel’espaced’arrivée ;si 2()
ker =f¡! 2(
¡!
)=¡! 0 g=
¡1³¡!
0
´
REM:ker vientdel’allemand”Kern”:noyau(introduitparHilberten1904),quiadonnél’anglais”kernel”:amande.
PROP:lenoyaud’uneapplicationlinéaireestunsous-espacevectorieldel’espacededépart.
D12
REM:cettepropositionestsouventutiliséepourdémontrerqu’unepartied’unevestenfaitunsev.
b)Exemples.
E4
c)Noyauetinjectivité.
LEMME:si 2()et ¡! 2 alorsladi¤érencededeuxsolutionsdel’équationd’inconnue ¡! 2:
():(
¡!
)=¡!
estunélémentdunoyaude 
REM:uneautrefaçondedirelamêmechoseestdedirequesi ¡! 0estunesolutionparticulièrede ()alorslesautres
solutionssontobtenuesenajoutantà¡!  0unélémentde ker ;sousformesymbolique:
¡1
(
¡!
)=¡!
0+ker 
CORO:si 2()et ¡! 2alors ¡1(¡! )est
soitvide
soitunsous-espacea¢nede dedirectionlenoyaude 
PROP:uneapplicationlinéaireestinjectivesietseulementsisonnoyauestréduitàzéro:
estinjective ,ker =f¡! 0g
D13
E5
2)Image.
3
PDF created with pdfFactory trial version www.pdffactory.com

COURSPCSI 10.ALGÈBRELINÉAIRE:APPLICATIONSLINÉAIRES R.FERREOL04/05
DEF:l’imaged’uneapplicationlinéaireestl’ensembledesimagesdesvecteursdel’espacededépart:
Im()=f
¡!
29
¡!
2(
¡!
)=¡! g=()
PROP:l’imaged’uneapplicationlinéaireestunsous-espacevectorieldel’espaced’arrivée.
D14
REM:pardé…nitiondelasurjectivité,uneapplicationlinéaireestsurjectivesietseulementsisonimageestégaleàson
espaced’arrivée:
estsurjective ,Im =
PROP:si BestunebasedeE, Im()=Vect((B)) 
E6
Bienretenirquelenoyaud’uneprojectionestsadirectionetquesonimageestsabase.
V)ISOMORPHISMES.
a)Isomorphismesetespacesisomorphes.
Rappelonsqu’unisomorphisme(d’espacesvectoriels)estuneapplicationlinéairebijective.
Nousnoterons  ()l’ensembledesisomorphismesde sur 
PROP:lacomposéededeuxisomorphismesestunisomorphisme,etlaréciproqued’unisomorphismeestunisomorphisme
:2 () 2 ())±2 ()
2 ())¡12 ()
D15
DEF:deuxespacesvectoriels et sontditsisomorphes(notation ¼)s’ilexisteunisomorphismede vers 
autrementdit:
¼, ()6=;
PROP:(corollairedelaprop.précédente):larelationd’isomorphie ¼estunerelationd’équivalenceentreespaces
vectoriels.
D16
Exempleimportant:si =© alors ¼£
D17
b)Isomorphismesetdimension.
LEMME:soit 2()B=(
¡!
1 ¡!
 )basede ,alors
estinjective(1) ,l’image ((¡! 1)(
¡!
)) de Bpar estunefamillelibrede (2)
estsurjective(3) ,l’image ((¡! 1)(
¡!
)) de Bpar estunefamillegénératricede (4)
estbijective(doncestunisomorphisme) ,
D18
THdecaractérisationdesespacesisomorphesendimension…nie:
Deuxespacesvectorielsdedimension…niesontisomorphessietseulements’ilsontlamêmedimension.
D19
VI)THÉORÈMESDELARESTRICTION,THÉORÈMEDURANG.
4
PDF created with pdfFactory trial version www.pdffactory.com

COURSPCSI 10.ALGÈBRELINÉAIRE:APPLICATIONSLINÉAIRES R.FERREOL04/05
1)Théorèmedelarestriction.
TH(delarestriction):larestrictiond’uneapplicationlinéaireàunsupplémentairedesonnoyaudé…nitunisomorphisme
decesupplémentairesursonimage,autrementdit
si (H):2(),=ker ©et 1:½!Im()
7! ()alors (C):
1estbijective,doncestunisomorphisme.
D20
REM:onpeutaussidiredefaçonéquivalentequelarestriction 0:½!
7! ()estinjectiveetque Im 0=Im 
COROLLAIRE1:unsupplémentairedunoyaud’uneapplicationlinéaireesttoujoursisomorpheàl’imagedecette
applicationlinéaire.
D21
COROLLAIRE2:deuxsupplémentairesd’unmêmesous-espacevectorielsonttoujoursisomorphes.
D22
2)Codimension,hyperplans.
TH:d’aprèslecorollaire2ci-dessus,siunsous-espacevectoriel de possèdeunsupplémentairededimension…nie,
touslesautressupplémentairesontlamêmedimension;cettedimensionestpardé…nitionla codimension de 
REM:si estdedimension…nie, codim =dim ¡dim 
DEF:unhyperplande estunsous-espacedecodimension1(autrementdit,unsous-espacedontunsupplémentaire
estunedroite).
Ex:endimension3,leshyperplanssontlesplans,maisendimension2,leshyperplanssontlesdroites...
3)Théorèmedurang.
THÉORÈMEDURANG:(applicationdirecteducorollaire1ci-dessus):lasommedesdimensiondunoyauetde
l’imaged’uneapplicationlinéaire(dontl’espacededépartestdedimension…nie)estégaleàladimensiondel’espacede
départ:
dimker +dimIm =dim  si dim +1
D23
COROLLAIRE1:ladimensiondel’imaged’uneapplicationlinéaireestinférieureouégaleàladimensiondel’espace
dedépart.
D24
COROLLAIRE2:uneapplicationlinéairediminuelesdimensionsausenslarge,plusprécisément:
si 2()sevDEDIMENSIONFINIEde ,alors
dim(()) 6dim 
D25
COROLLAIRE3pourqu’uneapplicationlinéaireentredeuxespacesDEMÊMEDIMENSION FINIE soitbijective,
ilsu¢tqu’ellesoitinjective(ouqu’ellesoitsurjective).
D26
E7
5
PDF created with pdfFactory trial version www.pdffactory.com