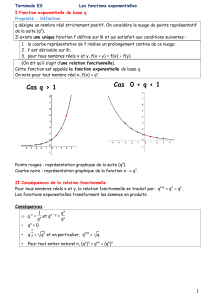
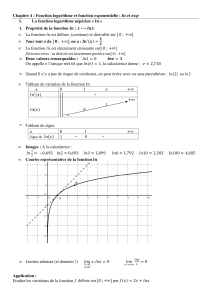
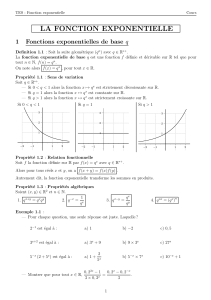
fonction exponentielle

La fonction exponentielle
Rémi CHEVAL
23 décembre 2013
Depuis un bon moment, j’ai cette fameuse question en tête : Comment expliquer les différentes
propriétés de la fonction exponentielle en n’utilisant que la définition ? Et aujourd’hui, j’ai de
l’inspiration donc allons-y et démontrons.
1 Définition de la notion
Définition 1 (Une fonctionne exponentielle). On appelle fonction exponentielle une fonction fdérivable
sur Ret vérifiant :
f′=f f(0)=1
Remarques :
– En écrivant cette définition, nous avons supposé qu’il existait effectivement une telle fonction.
– Or le problème de l’existence est assez complexe (voir problème de Cauchy et Théorème de Cauchy-
Lipschitz). Nous allons donc malheureusement devoir admettre qu’une telle fonction existe.
Objectif 2. (Unicité de la fonction exponentielle)
–Si nous supposons qu’il existe bien une fonction exponentielle,
–alors est-ce nous pouvons démontrer qu’elle est unique ?
Les bons réflexes du mathématicien :
– Dès lors que vous définissez un objet, il faut directement se poser la question de son existence et
son unicité. Ce sont des questions fondamentales et ne sont pas toujours évidentes à démontrer.
– Une fois l’unicité vérifiée, nous pourrons parler de LA fonction exponentielle.
2 Preuve de son unicité
Proposition 3. Soit exp une fonction exponentielle. Alors,
∀x∈R,exp(−x)∗exp(x)=1
Démonstration. Considérons la fonction gdéfinie sur Rpar : g(x)=exp(−x)∗exp(x).
1. Est-ce que gest dérivable sur R?On sait que exp est dérivable sur R. Ainsi gest dérivable sur
Rcar produit de fonctions composées dérivables sur R.
2. Démontrer que gest constante. Pour cela, il suffit de démontrer que g′est la fonction nulle.
Or ∀x∈R, g′(x)=−exp(−x) ∗exp(x)+exp(−x)∗exp(x)=0
3. Conclure.∀x∈R, g(x)=g(0)=exp(−0)∗exp(0)=1
Corollaire 4 (Une fonction exponentielle ne s’annule pas sur R).
1

Démonstration. Réalisons une preuve par l’absurde et supposons qu’il existe une fonction exponentielle fet
un réel atels que : f(a)=0. Nous obtenons que f(−a)∗f(a)=0: contradiction avec la proposition 3.
Théorème 5 (La fonction exponentielle est unique).
Les bons réflexes du mathématicien : Comment démontrer qu’un object est unique ?
– On suppose qu’il en existe deux et on montre qu’ils sont égaux.
Démonstration. On considère fet gdeux fonctions exponentielles et on démontre que f=g. Pour cela, on
considère la fonction hdéfinie sur Rpar h(x)=f(x)∗g(−x).
1. Vérifions que hest dérivable sur R:
On sait que fet gsont dérivables sur Rdonc hl’est aussi.
2. Calculons sa dérivée : ∀x∈R,
h′(x)=f′(x)∗g(−x)+f(x)∗−g′(−x) =f(x)∗g(−x)−f(x)∗g(−x)=0
3. Conclusion : ∀x∈R
h(x)=h(0)=1
Donc f(x)∗g(−x)=1
Donc f(x)=1
g(−x)car gne s’annule pas (corollaire 4.)
Donc f(x)=g(x)d’après la proposition 3.
À partir de maintenant, la fonction exponentielle sera toujours notée exp.
3 Propriétés de la fonction exponentielle
Proposition 6. ∀(x, y)∈R2,exp(x+y)=exp(x)∗exp(y)
Démonstration. On fixe le réel yet on considère la fonction fdéfinie sur Rpar :
f(x)=exp(x+y)
exp(y)
Il nous suffit alors de démontrer que : f=exp.
1. Est-ce que fest bien définie sur R?
D’après le corollaire 4, exp ne s’annule pas sur Rdonc fest bien définie sur R.
2. Est-ce que fest bien dérivable sur R?On sait que exp est dérivable sur R, donc fl’est aussi
car quotient de fonctions dérivables sur Ravec un dénominateur qui ne s’annule pas.
3. Calculons la dérivée de fsachant que exp(y)est ici une constante :
∀x∈R, f′(x)=1⋅exp′(x+y)
exp(y)=f(x)
4. Remarquons que : f(0)=1
5. La définition 1nous informe que fest une fonction exponentielle.
6. Le théorème 5nous informe que fest égale à exp.
2