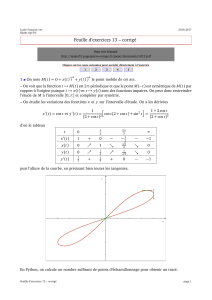
exo corige sur lp

MASTER SCIENCES
Mention Mathématiques et Applications -- ( 2M1MAP )
Expédition dans la semaine n° Etape Code UE N° d’envoi de l’UE
50 2M1MAP 2TMAP14 3
Nom de l’UE : Théorie de la mesure et Probabilités (UE 1-4)
–Contenu de l'envoi : Polycopié, chapitre 6. Corrigés des exercices du chapitre 6. Le polycopié est très
volumineux mais il contient beaucoup de résultats vus en Licence.
- Guide du travail à effectuer
Semaine 1 :
Etudier le chapitre 6, section 1 (Espaces Lp)
Exercices proposés (avec corrigés) : 6.7, 6.17, 6.18, 6.20
L' exercice 6.19 fait partie du deuxième devoir
Semaine 2 :
Etudier le chapitre 6, section 2 (Analyse hilbertienne, Espace L2)
Exercices proposés (avec corrigés) : 6.21, 6.24, 6.30, 6.31
Semaine 3 :
Etudier le chapitre 6, section 3 (Dualité)
Exercices proposés (avec corrigés) : 6.35 (sauf la question 3), 6.36
Semaine 4 :
Etudier le chapitre 6, section 4 (Convergence faible, étroite, en loi)
Exercices proposés (avec corrigés) : 6.48, 6.58, 6.55, 6.56
L' exercice 6.47 fait partie du deuxième devoir
Le deuxième devoir est à rendre à la réception du cinquième envoi
- Coordonnées de l'enseignant responsable de l'envoi
Thierry Gallouet, LATP-CMI, 39 rue Joliot Curie, 13453 marseille cedex 13.
email : [email protected]
fax : [phone]
Vous pouvez aussi consulter la page web: http://www.cmi.univ-mrs.fr/~gallouet/tele.d
et me poser des questions par email.
S e c r é t a r i a t : C e n t r e d e T é l é - E n s e i g n e m e n t S c i e n c e s U n i v e r s i t é d e P r o v e n c e
case 35 3, place Victor Hugo 13331 Marseille Cedex 03 Tél : [phone] Fax : [phone]
[email protected] http://www.ctes.univ-mrs.fr http://www.telesup.univ-mrs.fr
P o u r r a p p r o c h e r l a c o n n a i s s a n c e

Chapter 6
Les espaces Lp
6.1 D´efinitions et premi`eres propri´et´es
6.1.1 Les espaces Lp,avec1≤p<+∞
Soient (E,T, m) un espace mesur´e, 1 ≤p<∞et f∈M=M(E,T) (c’est-`a-dire f:E→R,
mesurable). On remarque que |f|p∈M
+, car |f|p=ϕ◦fo`u ϕest la fonction continue (donc bor´elienne)
d´efinie par ϕ(s)=|s|ppour tout s∈R. La quantit´e |f|pdm est donc bien d´efinie et appartient `a R+.
Ceci va nous permette de d´efinir les espaces de fonctions de puissance p-i`eme int´egrable. On retrouve,
pour p= 1, la d´efinition de l’espace des fonctions int´egrables.
D´efinition 6.1 (Les espaces Lp)Soient (E,T, m)un espace mesur´e, 1≤p<∞et fune fonction
d´efinie de Edans R,mesurable.(Onadonc|f|p∈M
+.)
1. On dit que f∈L
p=Lp
R(E,T, m)si |f|pdm < ∞.Onposealors:
fp=|f|pdm1
p.(6.1)
2. On dit que f∈ Lp=Lp
R(E,T, m)si |f|pdm =∞et on pose alors fp=+∞.
De mani`ere analogue au cas p= 1 on quotiente les espaces Lppar la relation d’´equivalence “= p.p.”
afin que l’application f→ fpd´efinisse une norme sur l’espace vectoriel des classes d”equivalence (voir
section 4.5).
D´efinition 6.2 (Les espaces Lp)Soient (E,T, m)un espace mesur´e et 1≤p<+∞.
1. On d´efinit l’espace Lp
R(E,T, m)comme l’ensemble des classes d’´equivalence des fonctions de Lp
pour la relation d’´equivalence (= pp).Enl’absenced’ambigu
¨
ıt´e on notera Lpl’espace Lp
R(E,T, m).
2. Soit F∈Lp
R(E,T, m).OnposeFp=fpsi f∈F.(Cetted´efinitionestcoh´erentecarne
d´epend pas du choix de fdans F.OnrappelleaussiqueF=˜ f={g∈L
p;g=fp.p.}.)
Proposition 6.1 Soient (E, T, m)un espace mesur´e et 1≤p<+∞.Alors:
1. Lp
R(E,T, m)est un espace vectoriel sur R.
131

2. Lp
R(E,T, m)est un espace vectoriel sur R.
D´ emonstration :
1. •Soit α∈R,f∈L
p.Onaαf∈M(car Mest un espace vectoriel) et |αf|pdm =
|α|p|f|pdm < ∞. Donc, αf∈L
p.
•Soit f,g ∈L
p. On veut montrer que f+g∈L p. On sait que f+g∈M(car Mest un espace
vectoriel) et on remarque que, pour tout x∈E,
|f(x)+g(x)|p≤2p|f(x)|p+2
p|g(x)|p,
et donc |f+g|pdm ≤2p|f|pdm +2
p|g|pdm < ∞,
ce qui montre que f+g∈L
p.
2. La structure vectorielle de Lps’obtient comme pour p= 1. Soit F, G ∈Lpet α,β∈R. On choisit
f∈Fet g∈Get on d´efinit αF+βGcomme ´etant la classe d’´equivalence de αf+βg. Comme
d’habitude, cette d´efinition est coh´erente car la classe d’´equivalence de αf+βgne d´epend pas des
choix de fet gdans Fet G.
On va montrer maintenant que f→ fpest une semi-norme sur λpet une norme sur Lp.
Lemme 6.1 (In´egalit´e de Young) Soient a, b ∈R+et p, q ∈]1,+∞[t.q. 1
p+1 q=1.Alors:
ab ≤ap
p+bq q.(6.2)
D´ emonstration :
La fonction exponentielle θ→ exp(θ) est convexe (de Rdans R). On a donc, pour tout θ1,θ
2∈Ret tout
t∈[0,1],
exp(tθ1+(1−t)θ2)≤texp(θ1)+(1−t)exp(θ2).
Soit a, b > 0 (les autres cas sont triviaux). On prend t=1
p(de sorte que (1 −t)=1 q), θ1=pln(a)et
θ2=qln(b). On obtient bien ab ≤ap
p+bq q.
Lemme 6.2 (In´egalit´e de H¨ older)
Soient (E,T, m)un espace mesur´e et p, q ∈]1,+∞[t.q. 1
p+1 q=1.Soientf∈L
p
R(E,T, m)et g∈
Lq
R(E,T, m).Alors,fg ∈L
1
R(E,T, m)et
fg1≤fpgq.(6.3)
Le mˆeme r´esultat est vrai avec Lp,Lqet L1au lieu de Lp,Lqet L1.
132

D´ emonstration :
On remarque d’abord que fg ∈Mcar f, g ∈M(voir la proposition 3.5).
L’in´egalit´e de Young donne |f(x)g(x)|≤|f(x)|p
p+|g(x)|q qpour tout x∈E. On en d´eduit, en int´egrant :
|fg|dm ≤1
p|f|pdm +1 q|g|qdm < ∞.(6.4)
Donc, fg ∈L
1.
Pour montrer (6.3), on distingue maintenant 3 cas :
Cas 1. On suppose fp= 0 ou gq= 0. On a alors f= 0 p.p. ou g=0p.p.. Onend´eduitfg =0p.p.,
donc fg1= 0 et (6.3) est vraie.
Cas 2. On suppose fp=1etgq= 1. On a alors, avec (6.4),
fg1=|fg|dm ≤1
p+1 q=1=fpgq.
L’in´egalit´e (6.3) est donc vraie.
Cas 3. On suppose fp>0etgq>0. On pose alors f1=f
fpet g1=g gq, de sorte que f1p=
g1q= 1. Le cas 2 donne alors
fg1
fpgq
=f1g1≤1.
Ce qui donne (6.3).
Dans le cas o`u f∈Lpet g∈Lq, on confond les classes fet gavec des r´epresentants, encore not´es fet
g. Le r´esultat pr´ec´edent donne fg ∈L
1et (6.3). On a alors fg ∈L1au sens de la confusion habituelle,
c’est-`a-dire “il existe h∈L
1t.q. fg =hp.p.” (et fg ne d´epend pas des repr´esentants choisis), et (6.3)
est v´erifi´ee.
Lemme 6.3 (In´egalit´e de Minkowski) Soient (E, T,m)un espace mesur´e et 1≤p<∞.Soient
f,g ∈L
p
R(E,T, m).Alors,f+g∈L
pet :
f+gp≤fp+gp.(6.5)
Le mˆeme r´esultat est vrai avec Lpau lieu de Lp.
D´ emonstration :
Le cas p= 1 `a d´ej`a ´et´e fait. On suppose donc p>1. On a aussi d´ej`a vu que f+g∈L
p(proposition
6.1). Il reste donc `a montrer (6.5). On peut supposer que f+gp= 0 (sinon (6.5) est trivial).
On remarque que
|f+g|p≤FH +GH, (6.6)
avec F=|f|,G=|g|et H=|f+g|p−1.
133

On pose q=p
p−1, de sorte que 1 p+1 q= 1, F∈L
p,G∈L pet H∈L q(car f+g∈L p). On peut donc
appliquer l’in´egalit´e de H¨ older (6.3), elle donne
FH1≤FpHq,GH1≤GpHq.
On en d´eduit, avec (6.6),
|f+g|pdm ≤(fp+gp)(|f+g|pdm)1−1
p,
D’o`u l’on d´eduit (6.5).
Il est clair que le lemme est vrai avec Lpau lieu de Lp.
On en d´eduit la propri´et´e suivante:
Proposition 6.2 Soient (E, T, m)un espace mesur´e et 1≤p<∞.
1. L’application f→ fpest une semi-norme sur Lp.
2. L’application f→ fpest une norme sur Lp.Lp,munidecettenorme,estdoncuneespace
vectoriel (sur R)norm´e.
D´ emonstration :
•On a bien fp∈R+pour tout f∈L
p.
•On a d´ej`a vu que αfp=|α|fp, pour tout α∈Ret tout f∈L
p.
•L’in´egalit´e (6.5) donne f+gp≤fp+gppour tout f, g ∈L
p.
L’application f→ fpest donc une semi-norme sur Lp. On remarque que, si f∈L
p, on a
fp=0⇔f=0p.p..
Cette ´equivalence donne que l’application f→ fpest une norme sur Lp.
Remarque 6.1 On reprend ici la remarque 4.9. Soient (E,T, m) un espace mesur´e et 1 ≤p<∞.On
confondra dans la suite un ´element Fde Lpavec un repr´esentant fde F, c’est-`a-dire avec un ´el´ement
f∈L
pt.q. f∈F. De mani`ere plus g´en´erale, soit A⊂Et.q. Acsoit n´egligeable (c’est-`a-dire Ac⊂B
avec B∈Tet m(B) = 0). On dira qu’une fonction f,d´efiniedeAdans R,estun´el´ementdeLpsi
il existe une fonction g∈L
pt.q. f=gp.p.. On confond donc, en fait, la fonction favec la classe
d’´equivalence de g, c’est-`a-dire avec ˜g={h∈L
p;h=gp.p. }. D’ailleurs, cet ensemble est aussi ´egal `a
{h∈L
p;h=fp.p. }.
Avec cette confusion, si fet gsont des ´elements de Lp,f=gsignifie en fait f=gp.p..
Th´eor`eme 6.1 (Convergence domin´ee) Soient (E,T,m)un espace mesur´e, 1≤p<∞,et(fn)n∈N
⊂Lpune suite t.q. :
•fn→fpp,
134