Exercice 1 La courbe représentative d`une fonction f est donnée ci

Exercice 1
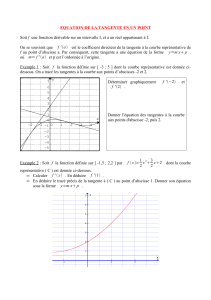
La courbe représentative d’une fonction f est donnée ci-après.
En chacun des points indiqués, la courbe admet une tangente qui est tracée.
1° En vous servant du quadrillage, compléter les égalités suivantes :
f (0) =
f ’(0) =
f (– 2) =
f ’(– 2) =
f (1) =
f ’(1) =
Exercice 2
1°Soit la fonction f définie sur [ 0 ; + [ par f (x) = x x et C est sa courbe représentative.
En revenant à la définition du nombre dérivé, montrer que f est dérivable en 0. Préciser f ’(0).
2° Déterminer l'équation de la tangente à Cf , au point d'abscisse 0
Exercice 3
f est la fonction définie sur IR par : f (x) = 3 x2 – 6 x + 1 et C est sa courbe représentative.
1° Démontrer que le taux de variations de f entre 2 + h et 2 est égal à 6 + 3 h.
2° En déduire le nombre dérivé de f en 2.
3° a) Démontrer que l'équation de la tangente T à C au point d'abscisse 2 est : y =6 x – 11.
b) Etudier la position de C par rapport à T.
Exercice 4
Soit la fonction f définie par : f (x) = 3 x – 1
2 – 3 x
Soit C f la courbe représentative de f dans le repère (O; i; j)
1° En utilisant la définition calculer le nombre dérivé de la fonction f au point a = 1
2° Déterminer l'équation de la tangente à Cf , au point d'abscisse a = 1
3° Etudier la position de la courbe Cf par rapport à la tangente à Cf , au point d'abscisse 1
4° Donner l'approximation affine de f (1 + h) pour h voisin de 0.
En déduire une valeur approchée de f (1,03) et de f (0,998)
Exercice 5
Soit la fonction f définie sur [ 0 ; 3] par : f (x) = x2
x + 1
1° En utilisant la définition calculer le nombre dérivé de la fonction f au point a = 2
2° Déterminer l'équation de la tangente à la courbe représentative de f au point d'abscisse 2
3° Donner l'approximation affine de f (2 + h) pour h voisin de 0. En déduire une valeur approchée de f (2,03) et de f
(1,998)
Exercice 6
Soit la fonction f définie sur [ – 1,5 ; + [ par : f (x) = 2 x + 3
1° En utilisant la définition calculer le nombre dérivé de la fonction f au point a = – 1
2° Déterminer l'équation de la tangente à la courbe représentative de f au point d'abscisse – 1
3° La fonction f est-elle dérivable en – 1,5
O
1
1
– 2

Exercice 1 La courbe représentative d’une fonction f est donnée ci-après. En chacun des points indiqués, la courbe admet une
tangente qui est tracée. 1° En vous servant du quadrillage, compléter les égalités suivantes :
f (0) = 1
f ’(0) = – 1
2
f (– 2) = – 1
f ’(– 2) = 0
f (1) = 3
2
f ’(1) = 2
Exercice 2
1° Soit la fonction f définie sur [ 0 ; + [ par f (x) = x x
En revenant à la définition du nombre dérivé, montrer que f est dérivable en 0. Préciser f ’(0).
f (0 + h) – f (0)
h = h h – 0 h = h
Par passage à la limite : lim
h  0 f(0 + h) – f (0)
h = lim
h  0 h = 0 = f ’(0).
2° Déterminer l'équation de la tangente à Cf , au point d'abscisse 0
f (0) = 0 et f '(0) = 0 donc la tangente
Exercice 3 f est la fonction définie sur IR par : f (x) = 3 x2 – 6 x + 1 et C est sa courbe représentative.
1° Démontrer que le taux de variations de f entre 2 + h et 2 est égal à 6 + 3 h.
f(2 + h) – f(2)
h = 3 (2 + h)2 – 6 (2 + h) + 1 – (3
22 – 6 2 + 1)
h = 3 (4 + 4 h + h2) – 12 + 1 – 6 h – 1 h
= 12 + 12 h + 3 h2 – 12 – 6 h
h = 3 h2 + 6 h h = 3 h + 6.
2° En déduire le nombre dérivé de f en 2.
f ' (2) = lim
h  0 f(2 + h) – f(2)
h = lim
h  0 (6 + 3 h) = 6 + 3
0 = 6.
3° a) Démontrer que l'équation de la tangente T à C au point d'abscisse 2 est : y =6 x – 11.
y = 1 + 6 (x – 2) y = 1 + 6 x – 12 y = 6 x – 11
b) d est la fonction définie sur IR par d(x)=f(x)–(6x–11). Etudier le signe de d(x) et en déduire la position de C par rapport à T.
d(x) = f (x) – (6 x – 11) = 3 x2 – 6 x + 1 – (6 x – 11) = 3 x2 – 6 x + 1 – 6 x + 11 = 3 x2 – 12 x + 12.
 = (– 12)2 – 4 3 12 = 0 . d(x) = 3 (x – 2)2 0
C est au dessus de T
Exercice 4 Soit la fonction f définie par : f (x) = 3 x – 1
2 – 3 x Soit C f la courbe représentative de f dans le repère (O;
i; j)
1° En utilisant la définition calculer le nombre dérivé de la fonction f au point a = 1
f (1 + h) – f (1)
h =
3 (1 + h) – 1
2 – 3 (1 + h) – 3 –1 2 – 3
h = 1 h × 
3 + 3 h – 1
2 – 3 – 3 h + 2 = 1 h × 
2 + 3 h
– 1 – 3 h + 2 (– 1 – 3 h) – 1 – 3 h = 1 h × 2 + 3 h – 2 – 6 h – 1 – 3 h
= – 3
– 1 – 3 h
Par passage à la limite on a donc f '(1) = lim
h  0 f (1 + h) – f (1)
h = lim
h  0 – 3
– 1 – 3 h = – 3 – 1 – 0 = 3
2° Déterminer l'équation de la tangente à Cf , au point d'abscisse a = 1
f (1) = 3 – 1
2 – 3 = – 2 et f '(1) = 3 donc l'équation de la tangente est : y = – 2 + 3 (x – 1)
y = 3 x – 5
3° Etudier la position de la courbe Cf par rapport à la tangente à Cf , au point d'abscisse 1
Il faut étudier le signe de f (x) – (3 x – 5)
f (x) – (3 x – 5) = 3 x – 1
2 – 3 x – (3 x – 5) = 3 x – 1 – (3 x – 5) (2 – 3 x) 2 – 3 x = 3 x – 1 – 6 x + 9 x2 + 10 – 15 x 2 – 3 x = 9 x2 – 18 x + 9 2 – 3 x
Pour étudier le signe de 9 x2 – 18 x + 9 = 9 (x2 – 2 x + 1) = 9 (x – 1)2
Pour tout réel x, 9 (x – 1)2 0 donc C f est au dessus de
4° Donner l'approximation affine de f (a + h) pour h voisin de 0.
Pour h voisin de 0 on a : f (a + h) f (a) + f '(a) × h Si a = 1 alors f (1 + h) – 2 + 3 h
En déduire une valeur approchée de f (1,03) et de f (0,998)
En posant h = 0,03 et f (1,03) – 2 + 3 × 0,03 donc f (1,03) – 1,91
En posant h = – 0,002 et f (0,998) – 2 + 3 × (– 0,002) donc f (0,998) – 2,006

Exercice 5 Soit la fonction f définie sur [ 0 ; 2] par : f (x) = x2
x + 1
1° En utilisant la définition calculer le nombre dérivé de la fonction f au point a = 1
Il faut calculer la limite quand h tend vers 0 de f (1 + h) – f (1)
h
f (1 + h) – f (1)
h =
(1 + h)2
1 + h + 1 – 1 2
h = 1 h × 2 (1 + 2 h + h2) – (2 + h) 2 (2 + h) = 1 h × 2 + 4 h + 2 h2 – 2 – h 2 (2 + h ) = 1 h × 2 + 4 h + 2 h2 – 2 – h 2 (2 + h )
= 1
h × 2 h2 + 3 h 2 (2 + h ) = 2 h + 3 2 (2 + h )
On a, par passage à la limite, f '(1) = lim
h  0 f (1 + h) – f (1)
h = lim
h  0 2 h + 3
2 (2 + h ) = 2 × 0 + 3 2 (2 + 0) = 3 4
2° Déterminer l'équation de la tangente à la courbe représentative de f au point d'abscisse 1
f (1) = 1
2 et f '(1) = 3 4 donc une équation de la tangente est y = 1 2 + 3 4 (x – 1) c'est à dire y = 3 4 x – 1 4
3° Donner l'approximation affine de f (1 + h) pour h voisin de 0. En déduire une valeur approchée de f (1,03) et de f (0,998)
f (1 + h) = 1
2 + 3 4 h
Pour h = 0,03 on obtient f (1,03) 1
2 + 3 4 × 0,03 donc f (1,03)
0,5225
Pour h = – 0,002 on obtient f (0,998) 1
2 – 3 4 × 0,002 donc f (0,998)
0,4985
Exercice 6 Soit la fonction f définie sur [ – 1,5 ; + [ par : f (x) = 2 x + 3
1° En utilisant la définition calculer le nombre dérivé de la fonction f au point a = – 1
f (1 + h) – f (1)
h = 2 (– 1 + h) + 3 – 2 × (– 1) + 3 h = 1 + 2 h – 1 h = 1 + 2 h – 1
h ( 1 + 2 h + 1) = 2 h h ( 1 + 2 h + 1) =
2
1 + 2 h + 1
Par passage à la limite on a : lim
h  0 f (1 + h) – f (1)
h = lim
h  0 2
1 + 2 h + 1 = 1.
2° Déterminer l'équation de la tangente à la courbe représentative de f au point d'abscisse – 1
f (– 1) = 1 et f '(– 1) = 1
Une équation de la tangente est donc y = 1 + 1 × (x + 1) c'est à dire y = x + 2.
3° La fonction f est-elle dérivable en – 1,5
On doit calculer la limite, si elle existe, de f (– 1,5 + h) – f (– 1,5)
h
f (– 1,5 + h) – f (– 1,5)
h = 2 (– 1,5 + h) + 3 – 2 × (– 1,5) + 3 h = 2 h h = 2 h
h 2 h = 2 2 h
La limite n'est pas finie donc il n'y a pas dérivabilité en – 1,5.