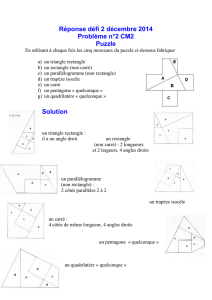
19 Novembre 2015 – Seconde 3 - Troisième interrogation de... 1 ) EFG semble être rectangle et isocèle. Exercice 1

19 Novembre 2015 – Seconde 3 - Troisième interrogation de mathématiques - CORRIGE
Exercice 1
1 ) EFG semble être rectangle et isocèle.
2 ) EFHG semble être un carré.
Exercice 2
1 )
2222 )129349()234344()()(  ABAB yyxxAB
.60500220110 22 
2 ) De même,
60500)110(220 22 AC
et
.000121)330(110 22 BC
On a donc AB = AC et ABC est isocèle en A.
De plus, AB2+AC2 = 121 000 = BC2 donc ABC est rectangle en A d’après la réciproque
de Pythagore. ABC est donc rectangle isocèle en A.
3 )
399
2454344 2
CB
Zxx
x
et
184
219349 2
CB
Zyy
y
.
4 ) On doit avoir Z milieu de A et D donc
399
2
234
2
DDA
Zxxx
x
et
184
2
129
2
DDA
Zyyy
y
d’où
184.2129
399.2234
D
D
y
x
d’où
564
D
x
et
239
D
y
.
5 ) Première façon : avec deux parallèles et une sécante, on a 4
angles égaux (voir à gauche). Ainsi si, par exemple,
 90
ˆ
A
,
on obtient
 90
ˆ
B
et
 90
ˆ
D
puis
 90
ˆ
C
.
Deuxième façon : par symétrie par rapport au centre,
DA ˆ
ˆ
et
CB ˆ
ˆ
donc s’il y a un angle droit il y en a deux. De plus
CBA ˆ
ˆ
ˆ
360
ˆ D
° d’où les deux autres angles droits.
6 ) ABDC est un parallélogramme avec un angle droit en A donc c’est un rectangle
d’après 5 ). C’est même un carré car AB=AC (deux côtés consécutifs de même longueur).
Exercice 3
1 ) Faux. JKLM a ses diagonales de même longueur mais ce n’est pas un rectangle.
2 ) est vraie.
3 ) Faux. Le quadrilatère STUV a des diagonales perpendiculaires et de même longueur
mais ce n’est pas un losange.
4 ) Faux. WXY a ses médianes concourantes (comme tout triangle) mais ce triangle n’est
ni équilatéral ni rectangle.
1,5
1
0.5
2
2
1
2
1
2
0,5
1
1
1
0,5
0,5
0,5
0,5
0,5
3
22