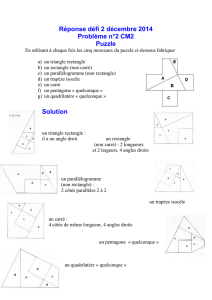
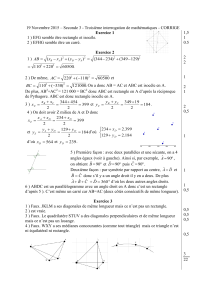
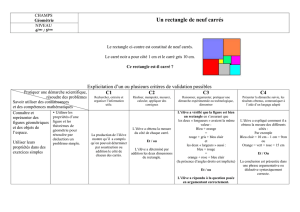
2) B = 49 18 10 (10 )

CORRECTION DU CONTROLE 1a (calculatrice interdite)
Exercice 1 : (sur 4 points) A faire sur cette feuille.
Dans le tableau suivant, entourer la ou les bonnes réponses.
Exercice 2 : (sur 3,5 points) A faire sur votre copie.
1)   
 2) B =
Calculer A et donner son écriture scientifique. Calculer B et l’écrire sous la forme d’une
fraction irréductible.
Exercice 3 : (sur 4,5 points) A faire sur votre copie
Développer puis réduire :
C = (x + 6)² D = (x – 2)(x + 3) + (3x – 5)²
C = x² + 2×x×6 + 6² D = x² + 3x – 2x – 6 + (3x)² – 2×3x×5 + 5²
C = x² + 12x + 36 D = x² + 3x – 2x – 6 + 9x² – 30x + 25
D = 10x² – 29x + 19
Exercice 4 : (sur 1,5 point) A faire sur votre copie.
On considère un triangle ABC rectangle en A tel que : AB = 4 m ; BC = 5 m
Calculer la longueur AC.
Dans le triangle ABC rectangle en A, l’égalité de Pythagore s’écrit :
BC² = BA² + AC²
5² = 4² + AC²
25 = 16 + AC²
AC² = 25 – 16
AC² = 9
Or AC est une longueur, elle est donc positive. D’où AC =
9
AC = 3 m.
Le nombre
…est-il égal à … ?
Le nombre
… est-il égal à… ?
1)
4)
2)
5)
3)
6)
A
C
B
5 m
4 m
E =       
E = 12x² + 8x – [(5x)² – 2²]
E = 12x² + 8x – 25x² + 4
E = –13x² + 8x + 4
2 3 4 2
B7 7 3 3
28
B7 21
68
B21 21
2
B21
5 3 4
2
5 3 4
2
5 12 2
5
6
49 18 10 (10 )
A14 10
7 7 2 9 10 10
A7 2 10
A 63 10
A 63 10
A 6,3 10
(écriture scientifique du nombre A)

Exercice 5 : (sur 1 point) A faire sur votre copie.
La sonde Voyager 1 a récemment atteint les limites de notre système solaire après avoir
parcouru 18 milliards de km en 3 cent mille heures environ.
Donner l’écriture scientifique de la vitesse en km/h à laquelle s’est déplacé la sonde dans le
système solaire
18 milliards de km = 18 × 109 km
3 cent mille heures = 3 × 105 h
D’où la vitesse de la sonde :
99
9 5 4
55
18 10 18 10
V 6 10 6 10
3 10 3 10
La sonde s’est déplacé à 6×104 km/h dans le système solaire
(Sa vitesse réelle était plus proche de 55 000 km/h)
Exercice 6 : (sur 4 points) A faire sur votre copie.
1°- Calculer l’aire A1 du rectangle et l’aire A2 du carré lorsque x = 4 cm
Lorsque x = 4cm :
- Les côtés du rectangle R1 mesurent 13 cm (2× 4 + 5) et 10 cm (3×4 – 2)
Donc A1 = 13 × 10 = 130 cm²
- Les côtés du carré C2 mesurent 3 cm (4 – 1)
Donc A2 = 3² = 9 cm²
°- Donner une expression développée (et réduite) des aires A1 et A2.
A1 = (3x – 2) × (2x + 5) A2 = (x – 1)²
A1 = 6x² + 15x – 4x – 10 A2 = x² – 2×x×1 + 1²
A1 = 6x² +11 x – 10 A2 = x² – 2x + 1
Exercice 7 : (sur 1,5 point) Extrait du brevet 2013
L’affirmation suivante est-elle vraie ou fausse ? Justifier la réponse.
Affirmation :
Pour n’importe quel nombre entier n, (n + 1)² – (n – 1)² est un multiple de 4.
Développons l’expression A = (n + 1)² – (n – 1)²
A = n² + 2×n×1 + 1² – [n² – 2×n×1 + 1²]
A = n² + 2n + 1 – (n² – 2 n + 1)
A = n² + 2n + 1 – n² + 2n – 1
A = 4n
n étant un nombre entier, 4n (c’est-à-dire 4 × n) est bien toujours un multiple de 4.
L’affirmation est vraie.
Rectangle R1
2x + 5
3x – 2
Carré C2
x – 1