Théorème 3 : Dans un triangle rectangle, la mesure de la hauteur

Théorème 3 : Dans un triangle rectangle, la mesure de la
hauteur issue du sommet de l’angle droit est moyenne
proportionnelle entre les mesures des deux segments qu’elle
détermine sur l’hypoténuse.
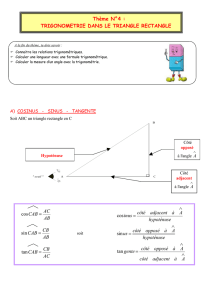
C'est à dire que dans un triangle
ABC
, rectangle en C, si la hauteur de l'angle C
rencontre
AB
en D , on aura :
DB CD
CD AD
=
Hypothèse :
ABC
rectangle en C . La hauteur issue de C coupe
AB
en D
Construction : Aucune.
Démonstration :
1.
CDA
∠
et
CDB
∠
sont des angles droits 1. Déf. de hauteur
2.
CAD CAD
∠ = ∠
et
CBA CBA
∠ = ∠
2. Identité
3.
ABC ACD
≈
et
ABC CBD
≈
3. Similitude A-A du triangle rectangle
4.
CBD ACD
≈
4. Transitivité
5.
DB CD
CD AD
= CQFD 5. Côtés homologues dans
CBD ACD
≈