Angles orientés : Exercices

Angles
orientés :
Exercices
I. Enoncé
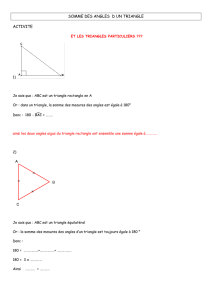
Soit la figure ci dessous où ABC est équilatéral direct , ACD et AEB
sont des triangles rectangles en E et D , isocèles directs.
Donner la mesure principale en radians de chacun des angles orientés
suivant:
(AB,
AC ) ; ( DC ,DA) ; (EB,EA) ; ( CB , CD ) ; (AE,AD) ; ( BC ,BE) ;
(EA,ED) ; (EA,
CB ) ; ( EC ,BA) ; ( EC ,DB)
II. Correction
! (AB,
AC )= π
ππ
π/3
en effet le triangle ABC est équilatéral donc tous les angles ont pour
mesure π/3 ; de plus (AB,
AC )suit le sens direct donc +π/3
! (
DC ,DA) = −
−−
−π
ππ
π/2,
attention l'angle ADC est droit mais dans le sens
indirect, d'où le signe moins
! (EB,EA) = +π
ππ
π/2
cette fois (EB,EA)est en sens direct
! (
CB , CD )
on utilise la relation de Chasles:
(
CB , CD ) = ( CB , CA)+(CA, CD )
(
CB , CA ) = -π/3 ; car ABC est équilatéral
(
CA , CD ) = -π/4; car ADC est rectangle et isocèle
d'où (
CB , CD ) = -π/3 - π/4 = -7π/12
! (AE,AD)
on décompose de même que précédemment :
(AE,AD) = (AE,AB) + (AB,
AC ) + ( AC ,AD) = π/4 + π/3 + π/4 =
10π / 12 = 5π/6
! (
BC ,BE) =( BC ,BA) + (BA, BE)= π
ππ
π/3 + π
ππ
π/4 = 7π
ππ
π/12
! (EA,ED)
le triangle AED est isocèle et (AE,AD) = 5π/6
donc (EA,ED) = (π-5π/6)/2= π/12
! (EA,
CB )
(EA, CB ) = (EA,EB) + (EB,BE) +
(BE,
BC ) + ( BC , CB ) = -π/2+π-7π/12+π
( attention au sens !!)
on a donc en mesure principale (EA,
CB )
=2π -π/2-7π/12=11π/12
! (
EC ,BA)
EA=EBdonc E appartient à la médiatrice de [AB]
De même CB=CA, donc C appartient à la médiatrice de [AB]
La médiatrice de [AB] est la droite (CE)
Ainsi (
EC ,BA) = +π/2 (sens direct)
! (
EC ,DB)
Dans le triangle BIC, rectangle en I , on a ( BC ,BI)= +π/3,
donc (
CI , CB )= π-π/3-π/2=π/6
On procède de même dans le triangle BJC, rectangle en J, et on
obtient : (
BC , BJ ) = +π/6
Ainsi : (
EC ,DB) = ( KC ,KB) = ( KC , CK ) + ( CK , CB ) + ( CB , BC )+
(
BC ,BK) + (BK,KB) = π + π/6 + π + π/6 + π = 10π/3
Soit en mesure principale -2π
ππ
π / 3
Remarque :
Tous ces exercices se ressemblent, il faut bien connaître les relations
du cours et faire attention aux sens des angles ( direct ou indirect).
MemoPage.com SA © / 2006 / Auteur : Claire Viano