03 - cours - Angles inscrits et polygones réguliers

Chapitre
6
Angles inscrits et polygones réguliers
I- Angle inscrit et angle au centre :
1°/ Vocabulaire :
Définition : Un angle dont le sommet est le centre d’un cercle est appelé angle au centre.
2°/ Propriétés :
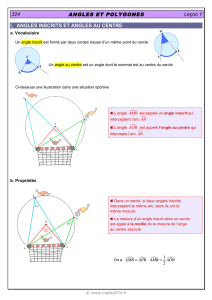
Propriété 1 : Dans un cercle, si un angle inscrit et un angle au centre interceptent le même arc de cercle,
alors la mesure de l’angle inscrit est égale à la moitié de l’angle au centre.
Propriété 2 : Si deux angles inscrits interceptent le même arc de cercle,
alors ils ont la même mesure.
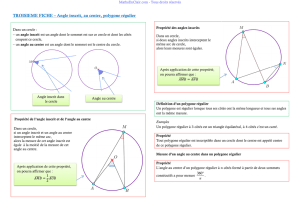
Comment calculer des angles dans une configuration complexe ?
Calculer ACD
puis BDC.
 Dans le cercle ( C ), on sait que :
• L’angle inscrit ACD et l’angle au centre
AOD interceptent le même arc AD.
Or d’après la propriété 1, on a :
Donc ACD = ½ AOD
= 130 : 2
= 65°.
 Dans le cercle ( C ), on sait que :
• BDA et BAC sont 2 angles inscrits qui
interceptent le même arc BC.
Or d’après la propriété 2, on a :
Donc BDA = BAC = 35°

II – Polygones réguliers :
.
1°/ Définition :
Illustration :
Définition : Un polygone dont tous les côtés ont la même longueur et dont tous les angles ont la même mesure est
appelé polygone régulier.
2°/ Propriétés :
Propriété 3 : Tous les sommets d’un polygone régulier appartiennent à un même cercle.
On dit qu’un polygone régulier est inscrit dans un cercle.
Le centre de ce cercle ( circonscrit au polygone ) est appelé centre du polygone régulier.
Propriété 4 : On considère un polygone à n côtés de centre O, n désignant un nombre entier positif.
Les points A et B sont deux sommets consécutifs de ce polygone.
L’angle AOB est appelé angle au centre du polygone régulier et sa mesure est égale à
n
°
360
.
Remarque : Le triangle équilatéral n’a pas de centre de symétrie.
Comment construire un pentagone régulier connaissant son centre et un sommet ?