POLYGONES ET ANGLES ANGLES Angle inscrit Définition : Un

POLYGONES ET ANGLES
I. ANGLES
1. Angle inscrit
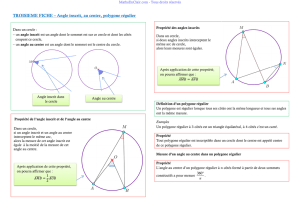
Définition : Un angle inscrit dans un cercle est un angle dont le sommet est sur le cercle et dont
les côtés coupent le cercle en deux points (distincts du sommet).
Exemple :
A, B, C désignent trois points d’un cercle.
ABC est un angle inscrit qui intercepte le petit arc d’extrémités A et C, noté AC.
2. Propriété
Si deux angles inscrits dans un cercle interceptent le même arc alors ils ont la même
mesure.
Exemple : BAL et BUL sont deux angles inscrits dans un cercle et interceptent le même arc BL,
donc ils ont la même mesure. BUL = BAL = 40°.
3. Angle au centre
A et C désignent deux points d’un cercle de centre O.
AOC est appelé angle au centre .
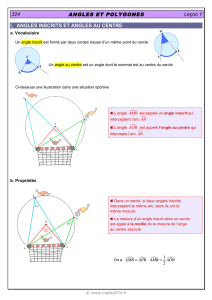
Propriété : Si un angle inscrit dans un cercle et un angle au centre interceptent le même arc
de cercle alors l’angle au centre mesure le double de l’angle inscrit.
O
B
A
C

II. POLYGONES REGULIERS
Définition : Un polygone est régulier lorsque tous ses côtés sont de même longueur et tous ses
angles sont de même mesure.
Exemples : Un triangle équilatéral est un polygone régulier à trois côtés ; un carré est un polygone
régulier à quatre côtés.
Propriétés :
Tout polygone régulier est inscriptible dans un cercle.
Tous les angles au centre déterminés par deux sommets consécutifs d’un polygone
régulier ont la même mesure.
B
A
C
C
D
A
B
E
D
C
B
A
E
A
C
B
D
F
B
A
H
G
F
ED
C
I
H
G
FED
C
B
A
K