Classe de cinquième Les triangles Propriété 1 SI deux

Classe de cinquième Les triangles
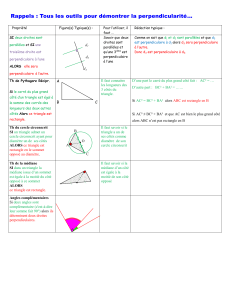
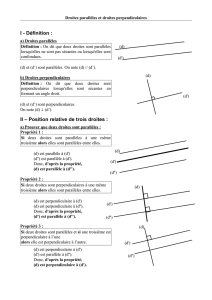
I PROPRIÉTÉS DES FIGURES FORMÉES PAR 3 DROITES :
Propriété 1
SI deux droites sont parallèles à une même droite,
ALORS ces deux droites sont parallèles entre elles.
Exemple :
On sait que :
(d1) // (d2)
(d2) // (d3)
PUISQUE les droites (d1) et (d3) sont parallèles à (d2),
ALORS d’après la PROPRIÉTÉ 1, (d1) et (d3) sont parallèles entre elles.
Propriété 2
SI deux droites sont perpendiculaires à une même droite,
ALORS ces deux droites sont parallèles entre elles.
Exemple :
On sait que :
(d1) ⊥ (d2)
(d1) ⊥ (d3)
PUISQUE les droites (d2) et (d3) sont perpendiculaires à (d1),
ALORS d’après la PROPRIÉTÉ 2, (d2) et (d3) sont parallèles entre elles.
Propriété 3
SI deux droites sont parallèles,
ALORS toute droite perpendiculaire à l’une est aussi
perpendiculaire à l’autre.
Exemple :
On sait que :
(d1) // (d2)
(d1) ⊥ (d3)
PUISQUE les droites (d1) et (d2) sont parallèles,
ALORS d’après la PROPRIÉTÉ 3, la droite (d3) qui est perpendiculaire à (d1) est aussi perpendiculaire
à (d2).
(d1)
(d2)
(d3)
(d1)
(d2)
(d3)
(d1)
(d2)
(d3)

II. SOMME DES ANGLES D’UN TRIANGLE.
a. Propriété :
La somme des angles d’un triangle vaut toujours 180°.
b. Conséquences :
Dans un triangle équilatéral, chaque angle mesure
60°.
Dans un triangle rectangle, les deux
angles aigus sont complémentaires.
III. CONSTRUCTIONS DE TRIANGLES.
(voir FICHE DE COURS)
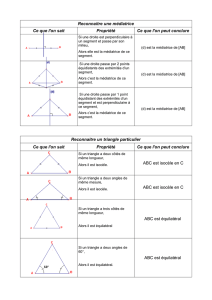
IV. CERCLE CIRCONSCRIT À UN TRIANGLE
a. Médiatrice d’un segment :
La médiatrice d’un segment [AB] est la droite (d) perpendiculaire à [AB] et qui passe par le
milieu I de [AB].
SI un M est un point la médiatrice de [AB],
ALORS M est équidistant (« à égale distance »)
de A et de B c’est à dire : MA = MB.
SI un point M est équidistant de A et de B,
ALORS M se trouve sur la médiatrice de [AB].
b. Cercle :
Le cercle de centre O et de rayon R (R est un NOMBRE) est l’ensemble de tous les points
situés à une distance R du point O.
c. Cercle circonscrit à un triangle :
Chaque triangle possède un cercle qui passe par ses 3 sommets. Son centre est O, le point de
concours des médiatrices des 3 cotés du triangle.
On dit que c’est le cercle circonscrit au triangle.
OA = OB = OC A
C
B
O

VI - INÉGALITÉ TRIANGULAIRE:
Soient 3 point A, B et C :
1 er cas : B n’est pas sur le segment [AC] :
alors AC < AB + BC
2 ème cas : B est sur le segment [AC] :
alors AC = AB + BC
CONCLUSION : dans tous les cas AC ≤ AB + BC
Conséquence : on ne peut construire un triangle que si la somme des longueurs de 2 côtés est
toujours supérieure à la longueur du 3ème côté.
Remarque : il suffit de regarder si le plus grand des côtés est inférieur à la somme des 2 autres.
EX : Peut-on construire ABC avec AB=6cm ; AC=3cm et BC=2cm ?
B
A
C
A
B
C