Document

Table des matières
Fonctions réciproques...........................................................................................................................3
Introduction......................................................................................................................................3
Définitions – Propriétés...................................................................................................................3
Fonctions injectives/surjectives – applications bijectives...............................................................5
Fonctions réciproques......................................................................................................................8
Exercices........................................................................................................................................11
Fonctions cyclométriques...................................................................................................................12
Définitions ....................................................................................................................................13
Fonction arc sinus.....................................................................................................................13
Fonction arc cosinus..................................................................................................................14
Fonction arc tangente................................................................................................................15
Et arc cotangente ?....................................................................................................................15
Exercices...................................................................................................................................16
Dérivation......................................................................................................................................16
Dérivation de arcsin x...............................................................................................................16
Dérivation de arccos x...............................................................................................................17
Dérivation de arctan x...............................................................................................................19
Exercices...................................................................................................................................20
Quelques identités fondamentales.................................................................................................20
sin(arcsin x)...............................................................................................................................20
arcsin(sin x)...............................................................................................................................21
cos(arccos x) ...........................................................................................................................21
arccos(cos x).............................................................................................................................22
Lien entre arcsin x, arcsin(-x), arccos x, arccos(-x)..................................................................23
cos(arcsin x) et sin(arccos x).....................................................................................................24
sin(arctan x)...............................................................................................................................25
tan(arccos x) .............................................................................................................................26
Résumé en un coup d'oeil..........................................................................................................28
Exercices...................................................................................................................................28
Équations cyclométriques..............................................................................................................28
Principe de résolution................................................................................................................28
Méthode de résolution...............................................................................................................30
Écrire correctement la CR d'une équation cyclométrique....................................................31
Équations en arcsin et arccos ...............................................................................................33
Équations en arctan..............................................................................................................33
Exemples...................................................................................................................................34
Exercices...................................................................................................................................40
Cas particulier : sommes et différences d'arc tangentes............................................................40
Une transformation utile.......................................................................................................40
Méthode complétée..............................................................................................................40
Astuce de calcul bien pratique..............................................................................................41
Exemples..............................................................................................................................42
1/49

Exercices..............................................................................................................................46
Démonstration d'identités cyclométriques.....................................................................................46
Méthode....................................................................................................................................46
Exercices...................................................................................................................................47
Règles de « de l'Hospital ».................................................................................................................48
Limite en un réel............................................................................................................................48
Limite en l'infini............................................................................................................................49
Exemples et remarques..................................................................................................................49
Exercices........................................................................................................................................50
Etudes de fonctions cyclométriques...................................................................................................51
2/49

Fonctions réciproques
Introduction
Définitions – Propriétés
Rappels TNI-20
•Une relation f d’un ensemble A vers un ensemble B est un triplet (A,B,G),
où
G⊂A×B
est appelé le graphe de la relation f
•Une fonction est une relation par laquelle chaque réel possède au plus une image :
La relation
f= ( A , B , G )
est une fonction
ssi
∀x∈A , ∀y , z ∈B: [ ( x ; y ) ∈G et ( x ; z ) ∈G ] ⇒y=z
ssi
∀x∈A , ∀y , z ∈B: [ f ( x ) =y et f ( x ) =z ] ⇒y=z
Réciproque d'une fonction
La relation réciproque d'une fonction réelle est la relation qui fait correspondre à
chaque réel y le ou les réels dont y est l'image par cette fonction. TNI-30
Définition équivalente :
Soient
A⊂ℝ , B⊂ℝ ,G f⊂A×B
: la relation réciproque de la fonction
f=
(
A , B , G f
)
est
la relation
g=
(
B , A ,G g
)
telle que
( x ; y ) ∈Gf⇔ ( y ; x ) ∈Gg
TNI-32
NB : Pour la facilité, nous convenons que lorsque l'on parlera de "réciproque" sans préciser,
on sous-entendra toujours "relation réciproque" et non « fonction réciproque »
Propriétés
Tout réel de dom f est appliqué sur un réel de Im f par la fonction f ; tout réel de Im f
est appliqué sur un ou plusieurs réels de dom f par la réciproque de f^.
TNI-34
En effet : tout réel de Im f est l'image d'au moins un réel de dom f, il a donc pour image par
la réciproque de f au moins un réel de dom f.
Dans un repère orthonormé, les graphes cartésiens de f et de sa réciproque sont
symétriques l'un de l'autre par rapport à la bissectrice du premier quadrant.
TNI-36
Stratégie de démonstration :
1. Démontrer que deux figures sont symétriques, cela revient à démontrer que pour
chaque point A de l'une, il y a un point de l'autre qui est le symétrique de A et
réciproquement.
2. Démontrer que deux points A et B sont symétriques par rapport à une droite d se fait
en distinguant 2 cas :
a) Les deux points sont confondus : dans ce cas, ils sont symétriques l'un
de l'autre si et seulement si ils appartiennent à d.
3/49

b) Les deux points sont distincts : dans ce cas, ils sont symétriques l'un
de l'autre si le segment qui les joint est perpenticulaire à d et si le
milieu de [AB] appartient à d.
Démonstration (selon cette stratégie):
Hypothèse :
A ( a ;b ) ∈Gf⇔f ( a ) =b⇔A' ( b ;a ) ∈Greciproque
. Il est donc déjà acquis qu'à chaque
point de Gf correspond un point A' de Greciproque et réciproquement.
Thèse :
A est le symétrique de A' par rapport à
d≡y=x
, la bissectrice du premier quadrant.
Démonstration :
Si A et A' sont confondus, alors a=b, A=A' est un point de d. Il est donc son propre
symétrique.
Si A et A' sont distincts, alors
a≠b
:
▪Le milieu du segment [AA'] a pour coordonnées
(
a+b
2;a+b 2
)
: c'est donc un
point de la bissectrice du premier quadrant.
▪Le coefficient angulaire du segment [AA'] vaut
yA ' −yA
xA ' −xA
=a−b
b−a=−1
, ce qui
est l'inverse de l'opposé du coefficient angulaire de d. [AA'] est donc
perpendiculaire à d.
Comme le raisonnement s'applique à tous les points de
Gf
, le symétrique de chaque
point de
Gf
appartient à
Greciproque
et inversement.
Le graphique de la réciproque de f est donc le symétrique du graphique de f par
rapport à la bissectrice du premier quadrant.
Comment faire pour trouver la réciproque d'une fonction ?
•Graphiquement: Dans un repère orthonormé, le graphe cartésien de la réciproque de
f est le symétrique du graphe cartésien de f par rapport à la bissectrice du premier
quadrant.
•Algébriquement :
1. On remplace x par y et y par x.
2. On exprime (si possible), y en fonction de x pour obtenir l'expression
analytique de la réciproque de f.
3. Au cours de ce processus, on rassemble les CE et les CR éventuelles, qui
servent à déterminer le domaine de définition de la réciproque.
Exemples
f:ℝ→ℝ:x→f
(
x
)
=x3
:
1.
y=x3
devient
x=y3
.
2. Isolons y :
y=3
√
x
4/49

3. Aucune CE ni CR n'a été rencontrée.
La réciproque de f est une fonction :
f−1:ℝ→ℝ:x→f−1 ( x ) =3
√
x
g:ℝ→ℝ:x→g
(
x
)
=x2
:
1.
y=x2
devient
x=y2
. On remarque donc que
x≥0
(CR).
2. Isolons y :
y=±
√
x
3. La réciproque de g n'est pas une fonction : c'est une relation h de
ℝ+
dans
ℝ
(on
n'écrira pas
h:ℝ+→ ℝ :
(
...
)
, ce type de notation étant réservé aux fonctions, et on ne
la désignera pas par g-1).
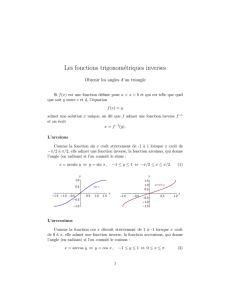
Figure 1: La réciproque de
la fonction "cube" est une
fonction.
Figure 2: La réciproque de la fonction
"carré" n'est pas une fonction.
(TNI-40) (TNI-50)
Fonctions injectives/surjectives – applications bijectives
On voit que les réciproques sont particulièrement intéressantes lorsque ce sont des fonctions, et que
cela dépend de caractéristiques de la fonction parfois délicates à exprimer clairement.
Un peu de vocabulaire pour nous comprendre...
Soit une fonction
f:A→B:x→f ( x ) ( A⊂ℝ , B⊂ℝ )
:
f est injective si et seulement si chaque élément de l'ensemble d'arrivée est l'image
d'au plus 1 élément de l'ensemble de départ. TNI-61
Ou encore (attention : on choisit des élément de dom f, pas de A!) :
.... si et seulement si deux réels distincts et quelconques de son domaine de
définition ont deux images différentes.
.... si et seulement si chaque réel de l'ensemble d'arrivée possède au plus un
antécédent.
.... ssi
∀x1, x2∈dom f :f
(
x1
)
=f
(
x2
)
⇒x1=x2.
.... ssi
∀x1, x2∈dom f :x1≠x2⇒f
(
x1
)
≠f
(
x2
)
.
5/49