DM futurs 1S 2015-016

A l’attention de tous les élèves de Première S pour l’année scolaire 2015-2016
DEVOIR MAISON DE MATHEMATIQUES
Un travail de révision (des grandes notions telles que les fonctions, les équations de droites, les vecteurs, les
probabilités, … ) est souhaitable pendant les grandes vacances pour une entrée solide en Première S.
Ce devoir est facultatif, cependant il permet de vous aider à retravailler certains chapitres abordés en Seconde
et de vous préparer aux premières notions qui seront traitées à la rentrée en septembre 2015.
En complément de ces révisions, ce devoir maison demande l’utilisation de certains logiciels qui est un des
points clairement signalés dans le programme ; il est donc important de s’y intéresser rapidement ( création
d’une figure dynamique sous GEOPLAN ou GEOGEBRA , d’une feuille de calcul sous OpenOffice ou EXCEL, … ).
Pour les élèves ayant fait ce devoir, la note ne sera prise en compte dans le calcul de la moyenne du
1
er
trimestre que si elle est à leur avantage. La copie sera ramassée, sans exception, lors du premier cours de
Mathématiques.
Nous utiliserons l’an prochain la plate-forme Edmodo sur laquelle vous devrez tous être inscrits* d’ici la
rentrée et par laquelle vous pourrez me poser des questions précises et m’envoyer les travaux informatiques
(notamment pour ce devoir maison).
Bonnes révisions et bonnes vacances à tous.
M
me
André
* Pour l’inscription sur Edmodo : indiquez vos nom et prénom, code de la classe : i4uzbh

Exercice 1
Un cycliste se rend d’une ville A à une ville B. Il effectue la moitié du trajet à 20 km/h et l’autre moitié
à  km/h. On rappelle la relation : v = d
t
1. a. Justifier que le temps t nécessaire pour effectuer la moitié du trajet à 20 km/h vérifie : t = AB
40.
b. Justifier de même que l’on a : t’ = AB
2 où t’ est le temps mis pour effectuer la moitié du trajet
à  km/h.
c. En déduire que la vitesse moyenne V(), en km/h, sur l’ensemble du trajet est : V() = 40
 + 20.
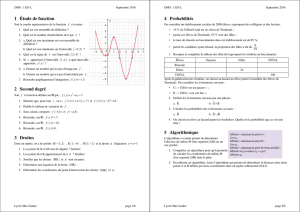
On donne ci-dessous une portion de la courbe de la fonction vitesse moyenne V :
2. Par lecture graphique et en laissant les tracés utiles sur le graphique :
a. Déterminer  pour que la vitesse moyenne soit de 24 km/h.
b. Déterminer toutes les valeurs de  pour lesquelles la vitesse moyenne est supérieure ou égale
à 15 km/h.
c. La vitesse moyenne semble-t-elle pouvoir dépasser 40 km/h ?
3. On souhaite maintenant retrouver algébriquement les réponses précédentes :
a. Déterminer  pour que la vitesse moyenne soit de 24 km/h en résolvant l’équation 40
 + 20 = 24.
b. Déterminer toutes les valeurs de  pour lesquelles la vitesse moyenne est supérieure ou égale
à 15 km/h.
c. Montrer que la vitesse moyenne ne peut pas dépasser 40 km/h.

Exercice 2 Position de trois droites
Dans un repère (O, I, J), on donne les points A(12 ; 0) , B(12 ; 8) et C(0 ; 8).
M est un point quelconque intérieur au rectangle OABC.
On trace par M les parallèles aux axes. Elles coupent les droites (OA), (AB), (BC) et (CO) respectivement
en D, F, E et G.
On souhaite étudier la position des droites (OB), (DF) et (EG) suivant la position de M à l’intérieur du
rectangle.
(exemple de figure)
Partie 1 : Expérimenter avec un logiciel de géométrie dynamique ( par exemple GEOGEBRA )
 FICHIER A ENVOYER en version électronique
1. Afficher la grille et créer les points A, B, C et O.
( Par exemple, pour A, dans la ligne de saisie, écrire : A = (12,0) )
2. Créer le rectangle OABC et la diagonale [AC].
3. Créer un point M quelconque intérieur au rectangle et les parallèles aux axes passant par M.
4. Créer les points D, F, E, G ainsi que les droites (OB), (DF) et (EG).
( par exemple, D sera défini comme l’intersection entre deux objets sur lesquels il faut cliquer )
5. Déplacer le point M à l’intérieur du rectangle. Quelle conjecture faites-vous concernant les droites
(OB), (DF) et (EG) suivant que M appartient ou non à la diagonale [AC] ?
Partie 2 : Démontrer dans deux cas particuliers
1
er
cas : On suppose que M a pour coordonnées (8 ; 4).
1. M appartient-il à [AC] ? Justifier.
2. Trouver l’équation réduite de chacune des droites (OB) et (DF). Justifier que ces droites sont
sécantes et déterminer les coordonnées de leur point d’intersection H.
3. Calculer les coordonnées des vecteurs
→
HE et
→
HG. Prouver que H, E, G sont alignés puis conclure
concernant les droites (OB), (DF) et (EG).
2
ème
cas : On suppose que M a pour coordonnées (9 ; 2).
1. Justifier que M est un point du segment [AC].
2. Par la méthode de votre choix, démontrer que les droites (OB), (DF) et (EG) sont parallèles.

Exercice3
Une expérience aléatoire consiste à lancer trois fois de suite un dé tétraédrique équilibré dont les 4 faces
sont numérotées 1; 2; 3; 4 et à compter le total de points obtenu.
1. On donne ci-dessous une ébauche de l’arbre de choix correspondant à cette expérience :
1 TOTAL : 3 points
2 TOTAL : 4 points
1 3 etc
2 4
1 3
4
2
3
4
a. Quelles sont toutes les valeurs possibles pour le total de points ?
b. Calculer la probabilité des événements : A : "on obtient 5 points exactement"
B : "on obtient au moins 11 points"
C : "on obtient au moins 4 points"
2. On considère l’algorithme suivant :
Variables
S, i, f des nombres
Début de l’algorithme
S prend la valeur 0
Pour i allant de 1 à 3
f prend la valeur d’un entier aléatoire entre 1 et 6
S prend la valeur S + f
FinPour
Afficher S
Fin de l’algorithme
a. Que représentent les variables f et S dans cet algorithme ?
b. Quel est le rôle de cet algorithme ?
c. Le programmer sous AlgoBox.  FICHIER A ENVOYER en version électronique