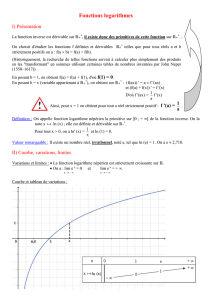
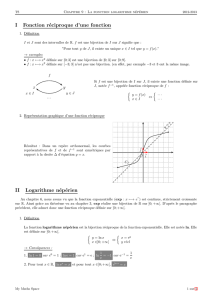
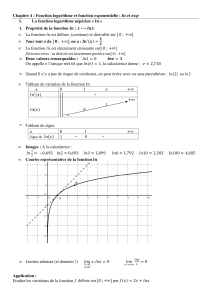
chapitre 3 logarithmes et exponentielles

Mathématiques 4e niveau 1 ANALYSE
Collège Sismondi (S.Z, base cours G.E.) 2014 - 2015 chapitre 3, p.1
CHAPITRE 3
LOGARITHMES ET EXPONENTIELLES
§ 3.1 Logarithmes
3.1.1 Introduction
Les règles de dérivation permettent de "deviner" les primitives de certaines fonctions.
Par exemple, nous savons que les fonctions fα : x ! xα ont pour dérivées f 'α : x ! αxα-1;
ceci signifie que ces fonctions fα ont pour primitives Fα : x !
x
α +1
α +1
+ C.
Mais l'écriture de Fα montre que cette fonction n'existe pas si α + 1 = 0, c’est-à-dire si α = -1 !
Donc les règles de dérivation ne nous permettent pas de trouver une primitive à la fonction
f : x !
1
x
de
€
R
+
*
dans
€
R
+
*
.
Pourtant, le théorème fondamental affirme que toute fonction continue sur un intervalle possède, sur cet
intervalle, une primitive.
Plus précisément, nous savons que les fonctions Fc : x !
f(t)dt
c
x
∫
où c ∈
€
R
+
*
sont toutes des primitives
de f : x !
€
1
x
sur tout intervalle fermé de
€
R
+
*
.
Nous allons étudier plus particulièrement la fonction F : x !
f(t)dt
1
x
∫
et montrer qu'il est possible de savoir
presque tout de cette fonction inconnue.
1.1.2 Etude d’une primitive de f : x !
1
x
Soit F : x !
f(t)dt
1
x
∫
.
Le théorème fondamental nous assure que F '(x) = f(x), c’est-à-dire que la fonction F est dérivable, mais
1 2 3 4
1
0.5
f

Mathématiques 4e niveau 1 ANALYSE
Collège Sismondi (S.Z, base cours G.E.) 2014 - 2015 chapitre 3, p.2
nous savons qu'une fonction dérivable sur un intervalle fermé est continue sur cet intervalle, donc la fonction
F est continue.
De plus, F '(x) = f(x) =
1
x
donc sur
€
R
+
*
, F '(x) > 0; ceci signifie que F est croissante.
La définition de l'intégrale permet d'affirmer que si a est inférieur à b, (resp. a supérieur à b) l'intégrale d'une
fonction positive de a à b est positive (resp. négative); appliquée à F, cette propriété montre que
si 0 < x < 1, alors F(x) =
f(t)dt
1
x
∫
< 0
si 1 < x, alors F(x) =
f(t)dt
1
x
∫
> 0
si x = 1, alors F(1) =
€
f(t)dt
1
1
∫
= 0 [ cf. prop. des intégrales ]
Donc le tableau des signes de la fonction F est :
x
0
1
+∞
F(x)
–
–
0
+
+
Pour pouvoir donner une esquisse de la fonction F, il nous faut encore déterminer son comportement aux
bornes de son domaine, c’est-à-dire lorsque x tend vers 0+ et vers +∞.
Pour cela nous allons calculer des approximations de F(n) =
f(t)dt
1
n
∫
où n est un nombre entier positif.
(Voir graphique page suivante)
Les rectangles hachurés sous la courbe de f ont des largeurs égales à 1 et des hauteurs valant res-
pectivement
1
2
,
1
3
,
1
4
,
1
5
, …
1
n
.
La somme des aires de ces rectangles vaut donc 1·
€
1
2
+ 1·
€
1
3
+ 1·
€
1
4
+ … + 1·
€
1
n
=
1
n
i=2
n
∑
ce qui signifie que F(n) =
f(t)dt
1
n
∫
>
1
n
i=2
n
∑
c’est-à-dire que pour tout n entier F(n) >
1
2
+
1
3
+
1
4
+ … +
1
n
Essayons d'évaluer la somme
f
1
1/2
1/3
1/4
1234 56

Mathématiques 4e niveau 1 ANALYSE
Collège Sismondi (S.Z, base cours G.E.) 2014 - 2015 chapitre 3, p.3
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
1
7
+
1
8
+
1
9
+
1
10
+
1
11
+
1
12
+
1
13
+
1
14
+
1
15
+
1
16
+
1
17
+
1
18
+ … +
1
n
en regroupant ses termes de la façon suivante :
1
2
!
"
#$
%
&
+
1
3
!+!1
4
!
"
#$
%
&
+
1
5
!+!1
6+1 7
!+!1
8
!
"
#$
%
&
+
1
9+... +1
16
!
"
#$
%
&
+
1
17 +... +1
32
!
"
#$
%
&
+ … +
1
n
c’est-à-dire un terme dans la première paire de parenthèses, deux dans la deuxième, quatre dans la troi-
sième, huit dans la quatrième, etc … , 2k-1 dans la ke paire de parenthèses.
Remarque :
Le dernier terme de la ke parenthèse est
1
2
k
; donc si m représente le nombre de parenthèses de la
somme ci-dessus, alors m est le plus grand entier tel que 2m ≤ n.
Il est alors possible d'évaluer le contenu de chacune de ces parenthèses :
1
3
+
1
4
>
1
4
+
1
4
= 2·
1
4
=
1
2
1
5
+
1
6
+
1
7
+
1
8
>
1
8
+
1
8
+
1
8
+
1
8
= 4·
1
8
=
1
2
la quatrième paire de parenthèses contient une somme de huit termes dont les sept premiers sont
strictement supérieurs au dernier; de cette constatation il découle que
1
9
+
1
10
+ … +
1
16
> 8·
1
16
=
1
2
la ke paire de parenthèses contient une somme de 2k-1 termes (le dénominateur du premier étant 2k-1+1 et
celui du dernier 2k) et tous ces termes sont supérieurs ou égaux au dernier ; donc
1
2
k−1
+1
+
1
2k−1+2
+
1
2
k−1
+3
+ … +
1
2
k
> 2k-1·
1
2
k
=
1
2
L'évaluation de ces parenthèses permet d'approximer F(n) :
F(n) =
f(t)dt
1
n
∫
>
1
n
i=2
n
∑
=
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
1
7
+
1
8
+
1
9
+
1
10
+
1
11
+
1
12
+
1
13
+
1
14
+
1
15
+
1
16
+
1
17
+
1
18
+ … +
1
n
=
1
2
!
"
#$
%
&
+
1
3
!+!1
4
!
"
#$
%
&
+
1
5
!+!1
6+1 7
!+!1
8
!
"
#$
%
&
+
1
9+... +1
16
!
"
#$
%
&
+
1
17 +... +1
32
!
"
#$
%
&
+ … +
1
n
>
1
2
+
1
2
+
1
2
+
1
2
+ … +
1
2
≥
m⋅1
2
Donc F(n) >
m⋅1
2
où m est tel que
2
m
≤n≤2
m+1
.
Mais alors, lorsque n tend vers l'infini, m doit aussi tendre vers l'infini; on obtient donc
lim
n→∞
F(n)= +∞
et donc
lim
x→∞
F(x)= +∞
.

Mathématiques 4e niveau 1 ANALYSE
Collège Sismondi (S.Z, base cours G.E.) 2014 - 2015 chapitre 3, p.4
Pour déterminer
lim
x→0
+
F(x)
, nous commencerons par remarquer que cette limite, si elle existe, doit être
négative, car on sait que F(x) < 0, si 0 < x< 1.
D'autre part et en valeur absolue, elle représente géométriquement l'aire d'une surface composée d'un carré
de côté égal à 1 et d'une figure délimitée par la courbe de f, l'axe des images et une droite horizontale
passant par 1.
La fonction f : x !
€
1
x
possède une intéressante propriété géométrique : en effet, on remarque facilement
que f(f(x)) = x, c’est-à-dire que f est sa propre réciproque. On sait que cela signifie que le graphique de f
possède une symétrie par rapport à la droite i : x ! x; la surface délimitée par la courbe de f, l'axe des
images et l'horizontale passant par 1 est donc symétrique de la surface délimitée par la courbe de f, l'axe
des x et la verticale passant par 1. Mais nous avons déjà vu que l'aire de cette dernière surface était infinie.
En conclusion,
lim
x→0
+
F(x)
=
−1⋅1+lim
x→∞
F(x)
( )
= -∞.
Les renseignements obtenus sur la fonction F permettent de tracer son graphique approximatif :
Définition
Nous appellerons logarithme naturel (et nous noterons ln)
la fonction de
€
R
+
*
dans R , définie par x !
1
t
dt
1
x
∫
ln(x) =
1
t
dt
1
x
∫
f
i
0 1
1
1
F
0

Mathématiques 4e niveau 1 ANALYSE
Collège Sismondi (S.Z, base cours G.E.) 2014 - 2015 chapitre 3, p.5
3.1.3 Propriétés caractéristiques du logarithme naturel
Nous allons montrer que le logarithme naturel défini au paragraphe précédent possède les mêmes
propriétés caractéristiques que les logarithmes définis dans le cours de 2e année.
Nous savons déjà que (ln(x))' =
1
x
.
1. ln(1) = 0 ln(x) < 0 si x < 1 et ln(x) > 0 si x > 1. (voir ci-dessus)
2. ln(ab) = ln(a) + ln(b)
Pour démontrer cette propriété, dérivons ln(ax).
ln'(ax) =
1
ax
. a =
1
x
= ln'(x)
D'où ln(ax) - ln(x) = c (constante), car 2 primitives d'une même fonction diffèrent d'une constante.
Prenons x = 1 pour déterminer cette constante : ln(a) - ln(1) = ln(a) - 0 = c.
Finalement : ln(ax) - ln(x) = ln(a)
Avec x = b, nous avons bien démontré la formule.
3. ln(
1
a
) = -ln(a) et ln(
a
b
) = ln(a) - ln(b).
En effet,
a⋅1
a
= 1 et
ln a⋅1
a
"
#
$%
&
'
) = ln(1) = 0
D'où ln(a) +
ln 1
a
!
"
#$
%
&
= 0 (propriété 2) et
ln 1
a
!
"
#$
%
&
= - ln(a).
Comme
a
b
=
a⋅1
b
, la deuxième égalité est immédiate.
4. ln(an) = n.ln(a) pour tout n ∈ Q.
On a
l! nx
n
( )
=
1
x
n
⋅nx
n−1
=
n⋅1
x
= n.ln'(x) =
n⋅ln(x)
( )
"
Donc
ln x
n
( )
- n.ln(x) = c (constante)
Choisissons x = 1 pour déterminer cette constante.
ln(1) - n.ln(1) = 0 ⇒ c = 0
On a donc :
ln x
n
( )
= n.ln(x) et en posant x = a, on obtient :
ln an
( )
= n.ln(a)