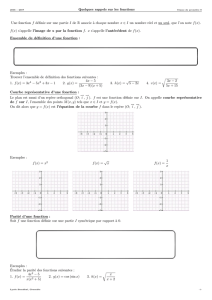
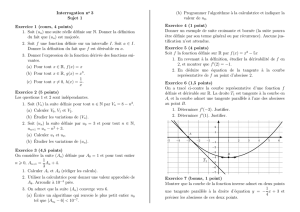
Opérations sur les fonctions

Ann´ee 2006-2007 1`ereSSI1
Chap 3 : Op´erations sur les fonctions
I. Vocabulaire
1) Courbe d’une fonction
D´efinition 1 : Soit fune fonction d´efinie sur un ensemble D. On appelle courbe repr´esentative de
f, dans un rep`ere O;−→
i;−→ jdu plan, l’ensemble des points Mde coordonn´ees
x;f(x), pour xdans D.
2) Restriction d’une fonction
D´efinition 2 : Soit fune fonction d´efinie sur un ensemble Dfet soit Iun intervalle de Rinclu
dans Df. La restriction de f`a Iest la fonction gd´efinie sur Ipar f(x) = g(x).
II. Comparaison de deux fonctions
1) Egalit´e de deux fonctions
D´efinition 3 : Soit fet gdeux fonctions d´efinies respectivement sur Dfet Dg.
f=g⇔Df=Dg
∀x∈ Df, f(x) = g(x).
2) Notation : f6g
D´efinition 4 : Soit fet gdeux fonctions d´efinies respectivement sur Dfet Dg.
Soit Iun intervalle inclu dans Dfet Dg.
f6gsur I⇐⇒ ∀x∈I, f(x)6g(x).
Page 1/5

Ann´ee 2006-2007 1`ereSSI1
Remarque : On d´efinit de mani`ere analogue f < g sur I,f > g sur Iet f>gsur I.
Repr´esentation graphique :
Soit Cfet Cgles courbes respectives de deux fonctions fet g.
f6gsur I⇔ Cfest en dessous de Cgsur I.
Les solutions de l’´equation f(x) = g(x) sont les abscisses des
points d’intersections des courbes Cfet Cg.
•
•
•
x
g(x)
f(x)
I
CgCf
D´efinition 5 : On dit que fest positive sur Dfet on note f>0 si pour tout xde Df, f (x)>0.
Interpr´etation graphique :
La courbe repr´esentative de la restriction de f`a Iest situ´ee au dessus de l’axe des abscisses.
Remarque : On d´efinit de mani`ere analogue f < 0 sur I,f > 0 sur Iet f>0 sur I.
D´efinition 6 : On dit qu’une fonction fest born´ee sur un intervalle I(inclu dans Df) s’il existe
deux nombres met Mtels que ∀x∈I, m 6f(x)6M.
Remarque : •Si ∀x∈I, f(x)6M, on dit que fest major´ee sur I.
•Si ∀x∈I, m 6f(x), on dit que fest minor´ee sur I.
•Si fest `a la fois major´ee et minor´ee sur I, elle est born´ee sur I.
Page 2/5

Ann´ee 2006-2007 1`ereSSI1
III. Op´erations sur les fonctions
1) Somme
D´efinition 7 : Soit fet gdeux fonctions d´efinies respectivement sur Dfet Dg.
La fonction f+gest la fonction d´efinie sur Df∩ Dgpar
∀x∈ Df∩ Dg,(f+g)(x) = f(x) + g(x).
2) Multiplication par un r´eel
D´efinition 8 : Soit fune fonction d´efinie sur Dfet α∈R.
La fonction αf est la fonction d´efinie sur Dfpar
∀x∈ Df,(αf )(x) = α×f(x).
3) Produit
D´efinition 9 : Soit fet gdeux fonctions d´efinies respectivement sur Dfet Dg.
La fonction f×gest la fonction d´efinie sur Df∩ Dgpar
∀x∈ Df∩ Dg,(f×g)(x) = f(x)×g(x).
4) Quotient
D´efinition 10 : Soit fet gdeux fonctions d´efinies respectivement sur Dfet Dg.
La fonction f
gest la fonction d´efinie sur Df∩ D∗
gpar
f
g(x) = f(x) g(x),
avec D∗
gl’ensemble des xde Dgpour lesquels g(x)6= 0.
Remarque : On d´efinit la fonction inverse 1
fde mani`ere analogue.
Page 3/5

Ann´ee 2006-2007 1`ereSSI1
5) Composition
D´efinition 11 : Soit fet gdeux fonctions d´efinies respectivement sur Dfet Dget telles que pour
tout xde Df:g(x)∈ Df.
La fonction f◦gest la fonction d´efinie sur Dgpar (f◦g)(x) = fg(x).
Elle se lit f(( rond )) g.
Exemple : Prenons fd´efinie sur R+par f(x) = √xet gd´efinie sur Rpar g(x) = x2+ 1. On a
bien g(x)∈ Dfpour tout xcar g(x)>1.
On peut donc d´efinir f◦gsur Rpar (f◦g)(x) = √x2+ 1.
Remarque : Il faut faire bien attention aux ensembles de d´efinition de f,get f◦g.
En g´en´eral, f◦g6=g◦f.
Exemple : Avec notre exemple pr´ec´edent :
(g◦f)(x) = √x2+ 1 = x+ 1 alors que (f◦g)(x) = √x2+ 1 et de plus f◦gest d´efini
sur Ralors que g◦fest quant `a lui d´efini sur R+.
IV. Sens de variation d’une fonction
1) D´efinition
D´efinition 12 : Soit fune fonction d´efinie sur Dfet I⊂ Df.
Si, pour tout r´eels x1et x2de Itels que x1< x2,
•f(x1)6f(x2), alors fest croissante sur I.
•f(x1)>f(x2), alors fest d´ecroissante sur I.
D´efinition 13 : Une fonction d´efinie sur Iest monotone sur Isi elle est croissante sur Iou si elle
est d´ecroissante sur I.
Minimum - Maximum :
•f(a) est le maximum de fsur Ilorsque pour tout xde I,f(x)6f(a)
•Mest un majorant de fsur Ilorsque pour tout xde I,f(x)6M.
•f(b) est le minimum de fsur Ilorsque pour tout xde I,f(x)>f(b)
•mest un minorant de fsur Ilorsque pour tout xde I,f(x)>m.
Remarque : Le maximum est un certain f(x) alors qu’un majorant pas forc´ement.
Page 4/5

Ann´ee 2006-2007 1`ereSSI1
2) Monotonie et Op´erations
Th´eor`eme 1 : Soit fmonotone sur Iet soit α∈R. Alors la fonction αf est monotone sur I.
Plus pr´ecis´ement :
•Si α > 0, alors fet αf sont de mˆeme monotonie.
•Si α < 0, alors fet αf sont de monotonie diff´erente.
−→ d´emonstration
Th´eor`eme 2 : Soient fet gdeux fonctions qui sont de mˆeme monotonie sur I. Alors la fonction
f+gest monotone sur I.
Plus pr´ecis´ement :
•Si fet gsont croissantes, alors f+gest croissante.
•Si fet gsont d´ecroissantes, alors f+gest d´ecroissante.
−→ d´emonstration
Th´eor`eme 3 : Soient get fdeux fonctions d´efinies sur Iet Jqui gardent la mˆeme monotonie
(avec pour tout xde I,g(x)∈J).
Alors la fonction f◦gest monotone sur I:
•Si fet gsont de mˆeme monotonie, alors f◦gest croissante.
•Si fet gsont de monotonie diff´erentes, alors f◦gest d´ecroissante.
−→ d´emonstration
Remarque : Ceci ne marche que pour la composition f◦get non pour le produit f×g.
Page 5/5