Fiche 3 - Martin DEL HIERRO

PTSI 07/08 Fiche n◦03
1 Définitions
Définition 1.1 On appelle application f, la donnée d’un triplet d’ensembles (E, F, Γ), où Γest
un sous-ensemble de E×F, que l’on appelle le graphe, et qui vérifie :
∀x∈E, ∃!y∈F|(x, y)∈Γ
Eest appelé l’ensemble de départ, Fest appelé l’ensemble d’arrivé ♠
Question: En considérant Γl’ensemble des couples (nom,âge) pris parmi les noms de l’ensemble
Edes élèves de PTSI et parmi leurs âges de l’ensemble F=N, a-t’on construit une application
(E, F, Γ) ?
Question: En considérant Γ0l’ensemble des couples (âge,nom), a-t’on construit une application
(F, E, Γ0)?
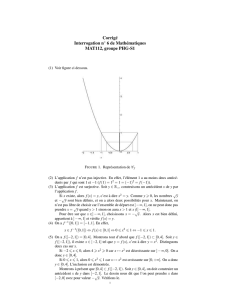
Exercice: Le diagramme ci-dessous correspond-t’il à une application ?
Remarque 1.1 Dans les faits on note : f:E−→ F
x7→ f(x)
Où f(x)est la donnée, pour chaque x∈E, de l’unique y∈Fqui vérifie (x, y)∈Γ.
f(x)est l’image de x, et xest un antécédent de f(x)∗
Exemple: On note IdE:E−→ E, l’application qui à tout x∈Eassocie x.
Lycée J-B. Say - Martin Del Hierro
1

PTSI 07/08 Fiche n◦03
Remarque: Attention f(x)n’est pas forcément donnée par une formule (voir exemple de la
valeur absolue ou de la partie entière). Et surtout, il ne faut pas oublier de préciser les ensembles
de départ et d’arrivée :
Soient f:R+−→ R
x7→ √x2et g:R−→ R
x7→ |x|
On a f6=g.
Définition 1.2 La collection des applications de Edans Fforme un ensemble que l’on note
FE.♠
Définition 1.3 (Restriction - Application Induite) Soit f= (E, F, Γ) une application.
Pour tout E ⊂ E, on note f|Ela restriction de fàEdéfinie par :
f|E= (E, F, ΓE)avec ΓE={(x, y)∈ E × F|(x, y)∈Γ}
Si de plus Fest une partie de Fvérifiant : ∀(x, y)∈Γ, x ∈ E =⇒y∈ F,
on définit l’application induite par fde Edans Fpar
(E,F,ΓE,F)avec ΓE,F={(x, y)∈ E × F | (x, y)∈Γ}
♠
Définition 1.4 (Composition) Soient f:E−→ Fet g:F−→ Gdeux applications, on
définit la composée de get de f, comme étant l’application g◦f:E−→ Gqui à x∈Eassocie
g(f(x)) dans G.
Ainsi on a : ∀x∈E; (g◦f)(x) = g(f(x)) ♠
En particulier si f:E→F, g :F→Get h:G→Hsont trois applications quelconques, on a
Associativité (h◦g)◦f=h◦(g◦f)
L’identité est un élément neutre pour la loi de composition :
f◦IdE=f IdF◦f=f
Remarque 1.2 Attention à ce que si g◦fa un sens, f◦gn’en a pas forcément. Et même si
cela avait un sens (G=E), en général :
g◦f6=f◦g
∗
Remarque 1.3 En toute rigueur, on ne devrait guère parler de composée pour des applications
f:E−→ Fet g:G−→ H
En revanche dans le cas où F⊂Gon définit g◦fdef =g|F◦f∗
2
Lycée J-B. Say - Martin Del Hierro

PTSI 07/08 Fiche n◦03
2 Bijectivité
l’assertion qui caractérise le graphe d’une application peut se réécrire comme1:
∀x∈E, ∃!y∈F|y=f(x)
Nous allons essayer de voir dans quels cas les rôles de Fet Epeuvent être échangés :
Pour y parvenir, il s’agit d’une part de vérifier la "taille" de l’ensemble d’arrivée. Si il est
suffisamment "petit" on a :
Définition 2.1 (surjectivité) Soit f:E−→ F, une application.
Lorsque tous les points de F, admettent au moins un antécédent par f, on dit que f est sur-
jective :
fest surjective ⇐⇒ ∀y∈F, ∃x∈E|y=f(x)
♠
Exemple: l’application partie entière R−→ Zest surjective.
En revanche l’application partie entière R−→ Rne l’est pas
D’autre part on vérifie la "taille" de l’ensemble de départ. Si il est suffisamment "petit" on
a :
Définition 2.2 (injectivité) Soit f:E−→ F, une application.
Lorsque tous les points de F, admettent au plus un antécédent par f, on dit que f est injective :
fest injective si et seulement si les points images2admettent un unique antécédent
mais aussi si et seulement si
∀(x, x0)∈E2hf(x) = f(x0)⇒x=x0i
ou encore si et seulement si
∀(x, x0)∈E2hx6=x0⇒f(x)6=f(x0)i
♠
1cette expression n’a pas de sens si on ne pose pas au préalable fcomme étant une application
2à ne pas confondre avec les points de l’ensemble d’arrivée
Lycée J-B. Say - Martin Del Hierro
3

PTSI 07/08 Fiche n◦03
Exemple: l’application valeur absolue R+−→ Rest injective.
En revanche la fonction valeur absolue R−→ Rne l’est pas.
En prenant la conjonction de ces deux propriétés, on en arrive à :
Définition 2.3 (bijectivité) Soit f:E−→ F, une application.
Lorsque tous les points de Fadmettent un unique antécédent par f, on dit que f est bijective :
fest bijective ⇐⇒ ∀y∈F, ∃!x∈E|y=f(x)
ce qui revient au même de dire que :
fest bijective si et seulement si fest à la fois injective et surjective. ♠
Exemple: l’application carrée R+−→ R+est bijective (voir Théorème de la bijection)
Exercice: le diagramme ci-dessous correspond-t’il à une application injective (resp. surjective,
resp. bijective) ?
Définition 2.4 (Application réciproque) A partir d’une fonction f= (E, F, Γf)bijective,
on peut construire une fonction dite réciproque, notée f−1, et dont le graphe est l’ensemble des
couples (y, x)∈F×E, où pour tout yélément de F,xest l’unique antécédent de ypar f.
f−1= (F, E, Γf−1)avec Γf−1=n(y, x)∈F×E|(x, y)∈Γfo
♠
Exercice: vérifier qu’il s’agit bien d’une application, et montrer qu’alors f−1est aussi bijective
et vérifie
³f−1´−1
=f
4
Lycée J-B. Say - Martin Del Hierro

PTSI 07/08 Fiche n◦03
Remarque 2.1 Une façon de caractériser la bijectivité d’une application fest de passer par son
application inverse, Ainsi :
fest bijective si et seulement si
Il existe une application g:F−→ Evérifiant
(∗)∀(x, y)∈E×F³y=f(x)⇐⇒ x=g(y)´
Et dans ce cas gest unique, c’est l’application réciproque f−1.
En particulier (*) est une caractérisation de la fonction réciproque. ∗
Exemple: l’application réciproque de l’application carré R+−→ R+, est ce qu’on appelle
l’application racine carrée, elle est caractérisée par
∀(x, y)∈(R+)2³y=x2⇐⇒ x=√y´
Proposition 2.1 Soit f:E−→ F, une application
Si f est bijective, son application réciproque est l’unique application g:F−→ Evérifiant
f◦g=IdFet g◦f=IdE
Réciproquement, s’il existe une telle application g, alors fest bijective et f−1=g♣
Exercice: Soient f:E→Fet g:F→Gdeux applications.
a) Montrer que g◦fsurjectif =⇒gsurjectif
b) Montrer que g◦finjectif =⇒finjectif
Remarque 2.2 On ainsi trouvé trois façons différentes de caractériser (resp. calculer) la bijec-
tivité (resp. l’application réciproque) d’un application donnée :
–Méthode Ensembliste : Définition 2.3
–Méthode Fonctionnelle : Remarque 2.1
–Méthode Algébrique : Proposition 2.1
Enfin on verra plus tard, avec le théorème de la bijection, une caractérisation particulièrement
simple pour les fonctions continues. ∗
Corollaire 2.2 Soient f:E−→ Fet g:F−→ Gdeux applications bijectives, on a alors :
g◦fest bijective et (g◦f)−1=f−1◦g−1
♣
Exemple: En posant
f:R+−→ R+
x7−→ x2et g:R+−→ [1,+∞[ x7−→ x+ 1
On a alors
g◦f:R+−→ [1,+∞[
x7−→ x2+ 1 et (g◦f)−1: [1,+∞[−→ R+ x7−→ √x−1
mais aussi
∀x∈[1,+∞[, f−1(g−1(x)) = √x−1
Question: Que peut-on dire de la composée de deux injections (resp. surjections) ?
Lycée J-B. Say - Martin Del Hierro
5