EX 1 : ( 2 points ) 1. Tracer dans le repère ci

EX1 : ( 2 points )
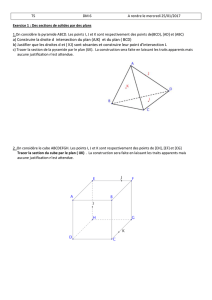
1. Tracer dans le repère ci-contre,
les droites d’équations :
D1:y=3x+2D2: 6x−2y= −2
D3:x=3D4:y= −3
D1passe par les points de coordonnées (0 ; 2) et (1 ; 5)
D2passe par les points de coordonnées (0 ; 1) et (1 ; 4)
D3passe par le point (3 ; 0) et D3(Oy)
D4passe par le point (0 ; −3) et D4(Ox)
2. Résoudre le système S0:(6x−2y= −2
y= −3.
Puis vérifier graphiquement cette résolution.
y
−4
−3
−2
−1
1
2
3
4
5
6
−5−4−3−2−1012345x
D1D2D3
D4
−4
3
S0:(6x−2y= −2
y= −3⇐⇒ (6x−2×(−3) = −2 y= −3⇐⇒ (6x+6= −2 y= −3⇐⇒ (6x= −8 y= −3⇐⇒ (x=−8
6=−4 3
y= −3
S=½µ−4
3;−3¶¾ Ce qui correspond bien, aux coordonnées du point d’intersection des droites D2et D4
EX2 : ( 2 points ) Résoudre les systèmes :
S1:(2x+3y=5
3x−y= −9S2:(3x−6y=9 −5x+10y= −16
ab0−a0b=2×(−1)−3×3= −11 6= 0.
Le système S1admet donc une unique solution.
Je résous ce système par combinaison sur les lignes :
(2x+3y=5
3x−y= −9×(3)
j’obtiens le système
équivalent :
(2x+3y=5
9x−3y= −27
j’ajoute membre à membre :
11x= −22
x=−22
11 = −2
(2x+3y=5×(3)
3x−y= −9×(−2)
j’obtiens le système
équivalent :
(6x+9y=15
−6x+2y=18
j’ajoute membre à membre :
11y=33
y=33
11 =3
le système S1admet une solution : S=n(−2 ; 3)o
ab0−a0b=3×10−(−5)×(−6) =0.
Le système S2n’admet pas une unique solution ;
il en admet soit aucune, soit une infinité.
Le système se réécrit aussi :
y=1
2x−3 2
y=1
2x−5 8
Ces deux droites sont parallèles et distinctes :
le système S2n’admet aucune solution : S= ;
2nde. Évaluation 7 - Correction ♣le 10-05-13

EX3 : ( 3 points )
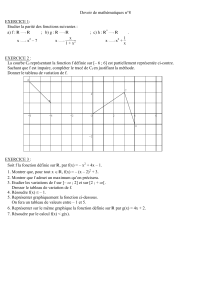
La figure ci-contre schématise une piscine formée à partir
de deux disques tangents de rayon R.
La piscine est entourée d’une surface rectangulaire revêtue
de dalles dont les bords sont situés à une distance mini-
mum ddes bords de la piscine.
La surface rectangulaire dont on dispose a les dimensions
L=10 m et l=6 m.
Calculer det R.
Les dimensions de l’ensemble imposent
les deux conditions :
(2d+4R =L=10 (en longueur) L1
2d+2R =l=6 (en largeur) L2
L
l
d
d
d d
RRRR
d
d
Pour ce système : ab0−a0b=2×2−2×4= −46= 0. Le système admet donc une unique solution.
Par combinaison L1−L2j’obtiens : 4R −2R =10−6⇐⇒ 2R =4⇐⇒ R=2
puis en utilisant L2: 2d+2×2=6⇐⇒ 2d=6−4⇐⇒ d=1
le système admet une solution : S=n(1 ; 2)od=1metR=2 m.
EX4 : ( 3 points )
On considère la fonction fdéfinie par
f(x)=x2+ax +b
où aet bsont des nombres réels
que l’on cherche à déterminer.
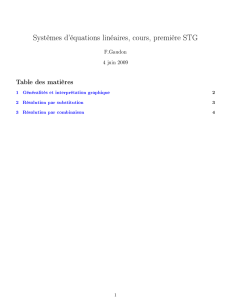
On souhaite que la courbe représentative Cfde cette
fonction f, passe par les points A(−1 ; 6) et B(1 ; 2).
1. Déterminer les réels aet bet donner l’expression de
la fonction fvérifiant ces deux conditions.
2. Donner la forme canonique de f, puis justifier à l’aide
de vos connaissances, le sens de variation de f.
Le point A(−1 ; 6) appartient à Cf, donc, f(−1) =6,
soit (−1)2+a(−1)+b=1−a+b=6.
De même le point B(1 ; 2) appartient à Cf, donc, f(1) =2,
soit 12+a×1+b=1+a+b=2.
−4−3−2−1 1 2 3 4
−1
1
2
3
4
5
6
7
8
x
y
O
A
B
Cf
En résumé, on a les deux équations :
(1−a+b=6
1+a+b=2⇐⇒ (−a+b=5 a+b=1
Pour ce système, ab0−a0b=(−1) ×1−1×1= −26= 0. Le système admet donc une unique solution.
La résolution du système donne a= −2 et b=3.
En remplaçant les valeurs trouvées pour aet bdans l’expression de f(x), on trouve donc l’expression : f(x)=x2−2x+3
La forme canonique de fest : f(x)=(x−1)2+2
La parabole de sommet B(1 ; 2)est tournée vers le haut car a>0,
la fonction fest décroissante sur ]−∞ ; 1]et croissante sur [1 ; +∞[
2nde. Évaluation 7 - Correction