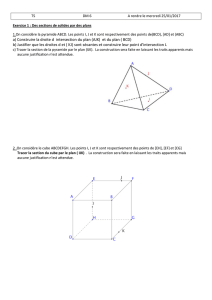
VAR à densité

ECE2 – Année 2016-2017
Chapitre 14 : Variables aléatoires à densité
1. Densité d’une V.A.R.
1.1 Fonction de répartition d'une variable à densité
Rappel : Soit X une VAR quelconque.
Sa fonction de répartition FX est définie par : x IR, FX(x) = P(X x).
On a alors :
_ FX est croissante sur IR,
_ FX est continue à droite en tout point.
_ lim
x +
FX(x) = 0, lim
x –
FX(x) = 1.
_ si a < b, P(a < X b) = FX(b) – FX(a).
Définition :
Soit X une V.A.R. de fonction de répartition FX.
Si FX est continue sur IR et de classe C1 sur IR sauf en un nombre fini de points, alors X est
une V.A.R. à densité.
Dans ce cas, toute fonction fx qui diffère de FX' en un nombre fini de points est appelé densité
de X.
Ex : Soit X une VAR dont la fonction de répartition est : FX(x) = 
 0 si x < 2
1 – 2
x si x
2
FX est continue et de classe C1 sur ]- ;2[ (fonction nulle) et sur ]2; + [ (différence d'une
constante et d'un quotient de fonctions affines).
lim
x  2, x <20 = 0 lim x  2, x 21 – 2
x = 0 donc FX est continue en 2.
Donc FX est continue sur IR et de classe C1 sur IR sauf en 2.
Donc X est une variable à densité.
FX'(x) = 
 0 si x < 2
2
x2 si x > 2 donc une densité de X est donnée par : fx(x) = 
 0 si x < 2
2
x2 si x
2
Propriété : Soit F une fonction définie sur IR. Si :
1) F est croissante sur IR,
2) lim
x +
F(x) = 0, lim
x –
F(x) = 1.
3) F est continue sur IR
4) F est de classe C1 sur IR, sauf en un nombre fini de points
alors F est une fonction de répartition d'une variable à densité X, et une densité est donnée par
la dérivée de F là où elle existe.
Remarque : Dans le cas où on ne sait pas que F est une fonction de répartition, il faut aussi
montrer que lim
x –
F(x) = 0, lim
x +
F(x) = 1 et F croissante sur IR.

ECE2 – Année 2016-2017
1.2 Densité de probabilité
Propriété :
Soit f une fonction définie sur IR. Si :
1) f est positive sur IR.
2) f est continue sur IR sauf en un nombre fini de points.
3) 
-
+
f(x)dx converge et vaut 1.
Alors f est une densité de probabilité d'une variable aléatoire X.
Exemple :
Soit f IR IR définie par : f(x) = 
 0 si x < 1
3
x4 si x
1
f est nulle sur ]- ;1[ et f(x) = 3
x4
0 sur [1 ;+ [. Donc f est positive sur IR.
f est continue sur ]- ;1[ (fonction nulle) et sur ]1 ; + [ (quotient de fonctions continues).
-
1 f(x)dx = 
-
1 0dx converge et vaut 0.
1+
f(x)dx =
1+
3
x4dx converge car 4 > 1 et 
1X 3
x4dx = 
1X 3x-4 = 
- 3x-3
3X
1 = - 1
X3 + 1
lim
x +
- 1
X3 + 1 = 1 donc 
-
+
f(x)dx converge et vaut 0 + 1 = 1.
Donc f est une densité de probabilité.
Propriété : TRES IMPORTANT
Soit X une variable aléatoire de densité de probabilité fX.
Alors x IR, FX(x) = P(X x) = 
-
x f(t)dt.
Exemple : Suite de l'exemple précédent :
Soit X une V.A.R. qui admet f comme densité de probabilité.
si x < 1, FX(x) = 
-
x f(t)dt = 
-
x 0dt = 0
si x 1, FX(x) = 
-
1 f(t)dt + 
1
x f(t)dt = 0 + 
1
x 3
t4dt = 1 – 1 X3.
Donc FX(x) = 
 0 si x < 1
1 – 1
x3 si x
1
Remarque : Quand on trouve FX, on vérifie toujours dans sa tête que : 
lim
x –
Fx(x) = 0
lim
x +
FX(x) = 1
FX continue sur IR
Propriété (Régularité de la fonction de répartition)
Si f est une densité de probabilité, alors la fonction FX : x
-
x f(t)dt est continue sur IR et
de classe C1 en tout point où f est continue, et en un tel point FX '(x) = f(x).
Plus généralement, si f est continue à droite (respectivement à gauche) en x, F est dérivable
à droite (respectivement à gauche) en x.

ECE2 – Année 2016-2017
Ex : suite de l'ex précédent
f est continue sur ]- ;1[ et sur ]1;+ [ donc F est de classe C1 sur ces deux intervalles et :
x < 1, F'(x) = 0, x > 1, F '(x) = 3
x4 (vérification : 1 – x-3
- (-3x-4) = 3
x4)
De plus, f est continue à droite en 1, donc F est dérivable à droite en 1.
1.3 Probabilité d'être dans un intervalle
Propriété :
Soit X une V.A.R. qui admet une densité de probabilité f.
Alors a IR, b IR avec a b,
1) P(X = a) = 0
2) P(X < a) = P(X a) = 
-
a f(t)dt (=FX(a))
3) P(X a) = P(X > a) = 
a+
f(t)dt. (= 1 – FX(a))
4) P(a X b) = P(a < X b) = P(a X < b) = P(a < X < b) = 
ab f(x)dx (= FX(b) – FX(a))
Illustration graphique (P(X a), P(a X b)
Ex : suite du premier ex :
P(X = 1) = 0 P(2 X 3) = 
23 f(t)dt = FX(3) – FX(2) = 
1 – 1
33 – 
1 – 1
23 = 1 8 – 1 27
P(X 1) = FX(1) = 0 P(X 2) = 1 – FX(2) = 1 –  1 – 1
8 = 1 8.
Remarques : _ donc, si I est un intervalle, alors P(X I) = 
I f(x)dx
_ si sur un intervalle I, f(x) = 0, alors P(X I) = 
I 0dx = 0.
_ inversement, si f(x) = 0 x IR \ I, alors P(X I) = 1,
Dans ce cas, on dit que X est à valeurs dans I.
On a alors : Fx(x) = 0 "avant I" et FX(x) = 1 "après I".
Exemple :
On a vu dans l'exercice 3 feuille 1 que f(x) = 
 0 si x < 0
2x si x [0,1]
0 si x > 1 est une densité de probabilité.
Si X est une VAR de densité f, alors X est à valeurs dans [0;1].
Et FX(x) = 0 si x < 0 et FX(x) = 1 si x 1.

ECE2 – Année 2016-2017
2. Moments d'une variable aléatoire à densité
2.1 Espérance
Définition :
Soit X une V.A.R. de densité f.
Si l'intégrale 
-
+
xf(x)dx est absolument convergente, on dit que X admet une espérance.
Dans ce cas, l'espérance de X est définie par : E(X) = 
-
+
xf(x)dx.
Ex : X de densité f(x) = 
 0 si x < 1
3
x4 si x
1
-
1 xf(x)dx = 
-
1 0dx converge et vaut 0.
1+
xf(x)dx =
1+
3
x3dx converge car 3 > 1, et :
T 1, 
1T 3
x3dx = 
1T 3x-3dx = 
-3
2x2T
1 = - 3
2T2 + 3 2 lim
T +
- 3
2T2 + 3 2 = 3 2 donc X admet une
espérance et E(X) = 0 + 3
2 = 3 2.
Rappel : si f est paire alors x xf(x) est impaire.
Dans cas si l'intégrale 
0+
xf(x)dx converge, alors X admet une espérance et E(X) = 0.
Théorème de transfert :
Soit X une V.A.R. qui admet une densité f nulle en dehors d'un intervalle ]a;b[ (avec - a <
b + ) et soit g une fonction continue sur ]a;b[ sauf en un nombre fini de points. La variable
aléatoire Y = g(X) admet une espérance si et seulement si l'intégrale
ab g(x)f(x)dx est absolument convergente. Dans ce cas, E(Y) = E(g(X)) =  ab g(x)f(x)dx.
Ex : suite de l'ex. précédent : E(X2), E(X3) ?
f est nulle en dehors de [1; + [.
1+
x2f(x)dx = 
1+
3
x2dx converge (absolument) et
T 1, 
1T 3
x2dx = 
- 3
xT
1 = - 3
T + 3.
lim
T +
- 3
T + 3 = 3 donc E(X2) existe et vaut 0 + 3 = 3.
_ 
1+
x3f(x)dx = 
1+
3
xdx diverge donc E(X3) n'existe pas.
Propriété : (Linéarité de l'espérance)
Soit X une V.A.R. à densité et a, b deux réels.
Si X admet une espérance, alors aX + b aussi et E(aX + b) = aE(X) + b.
2.2 Moment / Variance
Définition : Soit X une V.A.R. à densité et r IN.
Si Xr admet une espérance, on dit que X admet un moment d'ordre r, et on note mr(X) = E(Xr).

ECE2 – Année 2016-2017
Remarque : la fonction g(x) = xr est continue sur IR. Donc si 
-
+
xrf(x)dx est absolument
convergente, alors X admet un moment d'ordre r et mr(X) = 
-
+
xrf(x)dx.
Ex précédent : On a vu que X admet un moment d'ordre 1 et d'ordre 2, mais pas d'ordre 3.
Définition :
Soit X une V.A.R. à densité qui admet une espérance E(X). Si (X – E(X))2 admet une
espérance, alors on dit que X admet une variance.
La variance de X est alors : V(X) = E ( ) (X – E(X))2
l'écart-type de X est alors : (X) = V(X).
Propriété :
Soit X une V.A.R. à densité qui admet une espérance E(X). Alors V(X) existe si et seulement
si E(X2) existe. Dans ce cas; V(X) = E(X2) – E(X)2.
Ex : suite de l'ex précédent : E(X) = 3
2 E(X2) = 3 donc X admet une variance et
V(X) = E(X2) – E(X)2 = 3 – 9
4 = 3 4.
Propriété : Soit X une V.A.R. à densité et a, b deux réels.
Si X admet une variance, alors aX + b admet une variance et :
V(aX + b) = a2V(X) (aX + b) = a (X).
Définition :
Soit X une V.A.R. à densité.
Si X admet une espérance et si E(X) = 0, on dit que X est centrée.
Si X admet un écart-type et si (X) = 1, on dit que X est réduite.
Propriété :
Si X une V.A.R. à densité. d'espérance m et d'écart-type , alors X* = X – m
 est une variable
aléatoire centrée réduite.
Démonstration : E(X*) = E
X – m
 = E(X) – m  = m – m  = 0
(X*) = 
X – m
 = (X)
 = 1.