a) Construire la droite d intersection du plan (AJK) et du plan ( BCD

TS DM 6 A rendre le mercredi 25/01/2017
Exercice 1 : Des sections de solides par des plans
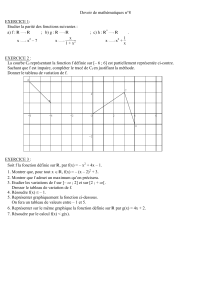
1.On considère la pyramide ABCD. Les points I, J et K sont respectivement des points de(BCD), [AD] et (ABC)
a) Construire la droite d intersection du plan (AJK) et du plan ( BCD)
b) Justifier que les droites d et ( KJ) sont sécantes et construire leur point d'intersection L
c) Tracer la section de la pyramide par le plan (IJK). La construction sera faite en laissant les traits apparents mais
aucune justification n’est attendue.
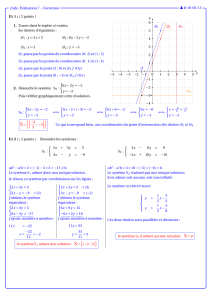
2 .On considère le cube ABCDEFGH. Les points I, J et K sont respectivement des points de [EH], [EF] et [CG]
Tracer la section du cube par le plan ( IJK) . La construction sera faite en laissant les traits apparents mais
aucune justification n’est attendue.

Exercice 2 :
Une ville compte 10 000 habitants. A 8 h du matin, 100 personnes apprennent une nouvelle.
On note
()ft
la fréquence des personnes connaissant la rumeur à l’instant t ( exprimé en heures ).
On choisit 8 heures, comme instant initial
0t
. La nouvelle se répand dans la ville de sorte que la vitesse de
propagation
'( )ft
est proportionnelle à la fois à la fréquence de ceux qui connaissent la nouvelle et à la fréquence de
ceux qui ne la connaissent pas. On admet que la fonction
f
vérifie la condition (1) :
'( ) 1,15 ( ) 1 ( )f t f t f t
quel que
soit
t
positif ou nul.
1. Expliquer pourquoi
(0) 0,01f
2. Montrer que la fonction
f
définie sur
0;
par
1,15
1
() 1 99 t ft e
vérifie la condition (1) et la relation
précédente. On admet que c’est la seule.
3. Etudier le sens de variation de
f
et déterminer sa limite en
4. Combien de personnes connaissent la nouvelle à midi ? On arrondira à l’entier .
5. Déterminer, par calcul, l’heure à laquelle au moins 99 % de la population connaîtra la rumeur
Exercice 3 :
Répondre par VRAI ou FAUX aux affirmations proposées, en justifiant vos réponses.
1.
2
ln4 ln 2 ln2
2. Soit
u
la fonction définie sur
0;
par
( ) 1 ln(2 )u x x x  
L’équation
( ) 0ux
admet une unique solution sur
0;
3. Soit (C) la courbe représentative de la fonction
f
définie sur
0;
par
( ) 1 lnf x x x
La tangente à (C) au point d’abscisse 1 admet comme équation
1yx
4. La suite
n
u
définie pour tout entier
n
non nul par
1
1 ln
nn
un
est décroissante.
5. Soit
f
la fonction définie sur
[0; [
par
2
( ) ln 1 2
x
f x x x   
.
Pour tout
x
de
0;
:
( ) 0fx
6.
2
2
3
lim ln 3
x
x
x
Exercice 4 : Pour chercher plus . Facultatif
1. Etudier le sens de variation de la fonction
f
définie sur
0;
par
ln
() x fx x
.
2. Comparer, pour n entier supérieur ou égal à 3, les nombres
1n
n
et
( 1)n n