développement limité résumé d'analyse 1 smpc s1 2019 2020

Développements limités
Notations du chapitre — Dans ce chapitre Iest un intervalle de R.
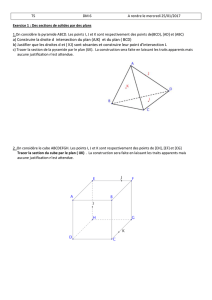
I — Définition
Définition 1.1 — Développement limité
On dit que la fonction f admet un développement limité à l’ordre nau voisinage
de x0 si et seulement si il existe une fonction polynôme P de degré au plus n telle
que, au voisinage de x0,
f(x) = P(x) + o((x−x0)n)
Propriété 1.2 — Unicité du développement limité
Si la fonction f admet un développement limité à l’ordre n au voisinage de x0 , alors
ce développement limité est unique.
Corollaire 1.3 — Si fadmet pour DL n(0)
f(x) = P(x)+ o(xn)
et si fest paire (resp. impaire), alors Pest également pair (resp. impaire).
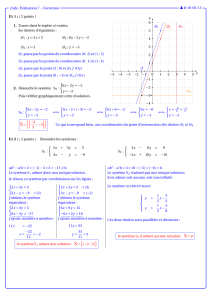
II — DL usuels
Théorème 2.1 — Formule de Taylor-Young
Soit f une fonction de I dans R , de classe Cn . Pour tout a et x dans I , il existe une
fonction εtelle que
f(x) =
n
X
k=0
(x−a)k
k!f(k)(a) + (x−a)n n!ε(x)
avec ε(x)−−→
x→a0.
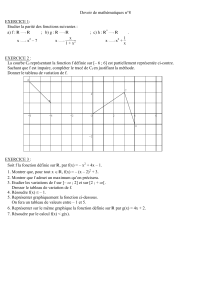
III — Opération sur les DL
Théorème 3.1 — Troncature
Si f admet un DL n(0) limité à l’ordre n de la forme a0 + a1x + · · · + anx + o ( xn ),
alors pour tout entier p¶n , f admet un DL p(x0) de la forme a0 + a1x + · · · +
apxp+o(xp)
Théorème 3.2 — Multiplication par un scalaire
Soit λ∈R . Si f admet pour DL n(0)f ( x ) = P ( x )+
o
( xn )alors λf admet comme
DL n(0)
λf(x) = λP(x)+ o(xn)
Ce document a été téléchargé gratuitement sur : www.marolet.ma

Théorème 3.3 — Addition
Si f et g admettent pour DL n(0)f ( x ) = P ( x )+
o
( xn )et g ( x ) = Q ( x )+
o
( xn )
alors f+gadmet comme DL n(0)
f(x) + g(x) = P(x) + Q(x)+ o(xn)
Théorème 3.4 — Multiplication
Si f admet pour DL n(0)f ( x ) = P ( x )+
o
( xn )et g admet un DL n(0)g ( x ) =
Q(x)+ o(xn)alors f×gadmet comme DL n(0)
f(x)×g(x) = P(x)×Q(x)
| {z }
tronqué à l’ordre n
+o(xn)
Théorème 3.5 — Primitive
Si fadmet pour DL n(0)
f(x) = a0+a1x+· · · +anxn+o(xn)
et si fadmet une primitive Fsur Ialors Fadmet comme DL n+1(0)(0)
F(x) = F(0) + a0x+a1
2x+· · · +an n+1xn+1+o(xn+1)
Théorème 3.6 — Composition
Si f admet pour DL n(0)f ( x ) = P ( x )+
o
( xn )et g admet un DL n(0)g ( x ) =
Q(x)+ o(xn)alors g◦fadmet comme DL n(0)
g(f(x)) = Q(P(x))
| {z }
tronqué à l’ordre n
+o(xn)
Ce document a été téléchargé gratuitement sur : www.marolet.ma