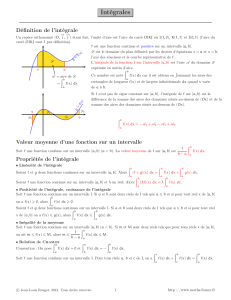
f (x)

TS. Contrôle 9 - Correction ♣
EX1 : ( 4 points ) Le but de cet exercice est de déterminer une valeur approchée à 10−2près de l’intégrale : I =Z1
0
e−x
2−xdx
1. a. Étudier les variations de la fonction f :x7−→ f(x)=e−x
2−xsur l’intervalle [0 ; 1].
Sur l’intervalle [0 ; 1], 2 −x6= 0, donc fquotient de fonctions dérivables est dérivable et :
f0(x)=−e−x(2 −x)+e−x
(2 −x)2=e−x(1 −2+x) (2 −x)2=e−x(x−1) (2 −x)2
Tous les termes sont positifs sur [0 ; 1] sauf x−1, donc f0(x)60 : la fonction fest décroissante sur [0 ; 1]
b. Montrer que, pour tout réel x de l’intervalle [0 ; 1], on a 1
e6f(x)61 2.
fest décroissante sur [0 ; 1] de f(0) =1
2àf(1) =e−1≈0,368 donc 1 e6f(x)61 2
2. Soit J et K les intégrales définies par J =Z1
0
(2 +x)e−xdx et K =Z1
0
x2f(x) dx.
a. Au moyen d’une intégration par parties, prouver que J =3−4
e.
Les fonctions sous le signe somme étant continues sur [0 ; 1], ainsi que leurs dérivées, on peut effectuer une
intégration par parties. Posons :
u0(x)=e−xu(x)= −e−x
v(x)=2+x v0(x)=1
u(x)v0(x)= −e−x
J=[−(x+2)e−x]1
0+Z1
0
e−xdx=£−(x+2)e−x−e−x¤1
0=£−(x+3)e−x¤1 0= −4e−1+3=3−4
e
b. Utiliser un encadrement de f (x)obtenu précédemment pour démontrer que 1
3e 6K61 6.
En partant de l’encadrement trouvé au 1. b. :
1
e6f(x)61 2⇐⇒ x2 e6x2f(x)61 2x2
d’où en intégrant sur [0 ; 1], Z1
0
x2
edx6K6Z1
0
1
2x2dx⇐⇒ ·x3 3e ¸1
0
6K6·x3
6¸1
0
⇐⇒ 1
3e 6K61 6
c. Démontrer que J +K=4I .
J+K=Z01(2 +x)e−xdx+Z1
0
x2e−x
2−xdx=Z1
0µ(2 +x)e−x+x2e−x
2−x¶dx=Z1
0
(2 −x)(2 +x)e−x+x2e−x
2−xdx
J+K=Z1
0
4e−x
2−xdx=4I
d. Déduire de tout ce qui précède un encadrement de I, puis donner une valeur approchéee à 10−2près de I .
Comme 1
3e 6K61 6et J=3−4 e
on a : 1
3e +3−4 e6J+K61 6+3−4 e⇐⇒ 3−11 3e 64I619 6−4 e⇐⇒ 1 4µ3−11 3e ¶6I61 4µ19 6−4 e¶
D’où 3
4−11 12e 6I619 24 −1 eor 3 4−11 12e >0,412 et 19 24 −1 e<0,424 on en déduit que 0,412 <I<0,424
il en résulte que I≈0,42 à 10−2près.
EX2 : ( 3 points ) On considère la suite (un)définie pour tout entier naturel n par : un=Z1
0
e−nx
1+e−xdx.
1. Montrer que u0+u1=1. Calculer u1. En déduire u0.
u0+u1=Z1
0
1
1+e−xdx+Z1
0
e−x
1+e−xdx
Par linéarité de l’intégrale, u0+u1=Z1
0
1+e−x
1+e−xdx=Z1
0
1 dx=[x]1
0=1

TS. Contrôle 9 - Correction ♣
u1=Z1
0
e−x
1+e−xdx. On pose f(x)=e−x 1+e−x, on remarque que f= − u0 uoù u(x)=1+e−x>0.
fa pour primitive F= − ln(u) donc u1=£−ln(1 +e−x)¤1
0=ln(2) −ln(1 +e−1)
D’après la question 1.a. u0=1−u1=1−ln(2) +ln(1 +e−1)=lne +ln(1 +e−1)−ln(2) =ln(e +1) −ln(2)
2. Montrer que pour tout entier naturel n,un>0.
Pour tout entier naturel n, et pour tout réel x, e−nx >0 et 1 +e−x>0 donc e−nx
1+e−x>0.
L’intégrale sur l’intervalle [0 ; 1] d’une fonction positive est positive donc unest positive ou nulle
3. a. Montrer que pour tout entier naturel n non nul, un+1+un=1−e−n
n.
Pour tout entier naturel n,
un+1+un=Z1
0
e−(n+1)x
1+e−xdx+Z1
0
e−nx
1+e−xdx=Z1
0
e−(n+1)x+e−nx
1+e−xdx=Z1
0
e−nx(e−x+1)
1+e−xdx
un+1+un=Z1
0
e−nx dx=·−1
ne−nx¸1
0
=1−e−n
n
b. En déduire que pour tout entier naturel n non nul, un61−e−n
n.
Pour tout entier naturel n, d’après la question 2. un>0 donc un+1>0
or, d’après la question 3. un=1−e−n
n−un+1donc un61−e−n n
4. Déterminer la limite de la suite (un).
Pour tout entier naturel n, 0 6un61−e−n
n. Or lim
n→+∞
1−e−n
n=0 (car e−ntend vers 0 ainsi que 1 n).
Selon le théorème des gendarmes, la suite unconverge aussi vers zéro
EX3 : ( 3 points ) Soit h la fonction définie sur par h(x)= − 1
2x2+2x−3 2.
Sur le graphique joint en annexe, le plan est muni d’un repère orthogonal ³O,−→ ı,−→ ´dans lequel on a tracé les courbes
représentatives des fonctions h et logarithme népérien sur l’intervalle [1 ; 4]. On a tracé également la droite (d)d’équation
x=4.
1. Démontrer que Z4
1
h(x) dx=0. Illustrer sur le graphique le résultat précédent.
hest continue sur comme fonction polynôme et :
Z4
1
h(x) dx=·−1
6x3+x2−3 2x¸4
1
=µ−1
6×64 +16 −6¶−µ−1 6+1−3 2¶= − 4 6+4 6=0
Sur le graphique, les deux aires hachurées sont égales.
~
~
ı1234
−1
1
x
y
O
(d)

TS. Contrôle 9 - Correction ♣
2. On note (D)le domaine du plan délimité par la droite (d)et les courbes représentatives des fonction h et logarithme
népérien sur l’intervalle [1 ; 4]. En utilisant un intégration par parties, calculer l’aire de (D)en unités d’aire.
Sur [1 ; 4], l’aire Adu domaine (D) est donnée par : A=Z4
1
(ln x−h(x)) dx=Z4
1
ln xdx−Z4
1
h(x) dx
par linéarité et compte-tenu du fait que Z4
1
h(x) dx=0. Les fonctions sous le signe somme étant continues sur
[1 ; 4], ainsi que leurs dérivées, on peut effectuer une intégration par parties. Posons :
u0(x)=1u(x)=x
v(x)=ln x v0(x)=1
x
u(x)v0(x)=x×1
x=1
D’où :
A=Z4
1
ln xdx=[xln x]4
1−Z4
1
1 dx=4ln4 −1×(4 −1) =8ln2 −3 u.a.