Integration

Intégrales
Définition de l’intégrale
Un repère orthonormé (O,
−→
i ,
−→
j)étant fixé, l’unité d’aire est l’aire du carré OIKJ où I(1, 0),K(1, 1)et J(0, 1)(l’aire du
carré OIKJ vaut 1par définition).
D
ab
y=f(x)
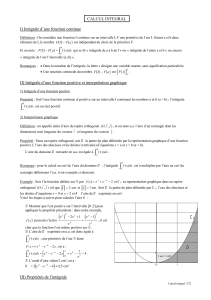
fest une fonction continue et positive sur un intervalle [a, b].
Dest le domaine du plan délimité par les droites d’équations x=aet x=b,
l’axe des abscisses et la courbe représentative de f.
L’intégrale de la fonction fsur l’intervalle [a, b]est l’aire Adu domaine D
exprimée en unités d’aire.
Ce nombre est noté Zb
a
f(x)dx car il est obtenu en Rommant les aires des
rectangles de longueur f(x)et de largeur infinitésimale dx quand xvarie
de aàb.
A=aire de D
=Zb
a
f(x)dx
a
b
D1
D2
D3
D4
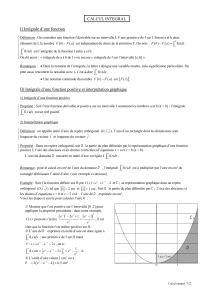
Si fn’est pas de signe constant sur [a, b], l’intégrale de fsur [a, b]est la
différence de la somme des aires des domaines situés au-dessus de (Ox)et de la
somme des aires des domaines situés au-dessous de (Ox).
Zb
a
f(x)dx = −A1+A2−A3+A4.
y=f(x)
Valeur moyenne d’une fonction sur un intervalle
Soit fune fonction continue sur un intervalle [a, b](a < b). La valeur moyenne de fsur [a, b]est 1
b−aZb
a
f(x)dx.
Propriétés de l’intégrale
•Linéarité de l’intégrale
Soient fet gdeux fonctions continues sur un intervalle [a, b]. Alors Zb
a
(f+g)(x)dx =Zb
a
f(x)dx +Zb
a
g(x)dx.
Soient fune fonction continue sur un intervalle [a, b]et λun réel. Alors Zb
a
(λf)(x)dx =λZb
a
f(x)dx.
•Positivité de l’intégrale, croissance de l’intégrale
Soit fune fonction continue sur un intervalle I. Si aet bsont deux réels de Itels que a6bet si pour tout réel xde [a, b]
on a f(x)>0, alors Zb
a
f(x)dx >0.
Soient fet gdeux fonctions continues sur un intervalle I. Si aet bsont deux réels de Itels que a6bet si pour tout réel
xde [a, b]on a f(x)6g(x), alors Zb
a
f(x)dx 6Zb
a
g(x)dx.
•Inégalité de la moyenne
Soit fune fonction continue sur un intervalle [a, b](a < b). Si met Msont deux réels tels que pour tous réels xde [a, b],
on ait m6f(x)6M, alors m61
b−aZb
a
f(x)dx 6M.
•Relation de Chasles
Convention : On pose Za
a
f(x)dx =0et Za
b
f(x)dx = − Zb
a
f(x)dx.
Soit fune fonction continue sur un intervalle I. Pour tous réels a,bet cde I, on a Zc
a
f(x)dx +Zb
c
f(x)dx =Zb
a
f(x)dx.
c
Jean-Louis Rouget, 2012. Tous droits réservés. 1 http ://www.maths-france.fr