Fonction Logarithme Népérien

Fonction Logarithme Népérien
Site MathsTICE de Adama Traoré Lycée Technique Bamako
I – Définition et conséquences :
1- Définition : la fonction logarithme népérien notée ln ou Log est la primitive
de la fonction x ֏
1
qui s’annule pour 1. Elle est définie sur ]0 ; +∞[.
x
2- Conséquence immédiates de la définition :
La fonction ln : ]0 ;+∞[ → ℝ est continue, et dérivable sur ]0 ; +∞[.
֏ lnx
x
II – Relation fonctionnelle fondamentale:
1- Propriété : ∀ (a ; b) ε (ℝ *+ )2 ; ln(a × b) = lna + lnb .
2- Conséquences :
a
b
C1) Soit a et b deux réels strictement positifs : ln( ) = lna – lnb .
a
alors a = bc ; lna = ln(bc) ⇒ lna = lnb + lnc ⇒
b
a
lnc = lna – lnb ⇔ ln( ) = lna – lnb .
b
1
C2) ∀a ε ℝ *+ ; ln ( ) = – lna .
a
En effet si c =
C3) ∀a ε ℝ *+ ; ∀n ε ℝ ; ln a n = n × lna .
C4)
lna = lnb
⇔
C5)
∀a ε ℝ *+ ;
ln a = ln a 2 =
a=b
;
1
lna ≤ lnb
⇔
a≤b.
1
lna .
2
III – Fonction du type (ln o u):
Soient u et v deux fonctions continues et dérivables sur un intervalle I.
1 – Propriétés des dérivées logarithmiques :
P1 )
(ln o u )ɅɅ(x) =
u ' ( x)
.
u ( x)
Exemples : a/ Soit f (x) = ln (x2 + 3x – 1) on a : f Ʌ(x) =
Cours Fonction logarithme
Page 1 sur 5
2x + 3
.
x + 3x − 1
2
Adama Traoré Professeur Lycée Technique
b/ Soit g : ] −
π
;
2
π
→ℝ
[
2
x ֏
g(x) = – ln (cosx)
on a
gɅ (x) =
− sin x
= tan x .
cos x
Donc une primitive de tanx est : – ln (cosx) .
P2 )
[ln ( u × v)]ɅɅ =
P3 )
[ln( )]ɅɅ =
u
v
u' v'
−
.
u v
2x − 1
−x+3
Exemple : f ( x) = ln
P4 )
u' v'
+
.
u v
[ln(U )] = r × UU '
r
⇒
f ' ( x) =
2
1
.
+
2x − 1 − x + 3
.
'
Exemple : f ( x) = ln( x + 3) 5
⇒
f ' ( x) = 5 ×
1
.
x+3
2 – Recherche de Primitives :
Une primitive de
Soit g(x) =
u'
u
est
ln u + c
.
1
2x
on a G(x) = ln |x| + c ; h(x) = 2
⇒ H(x) = ln |x2 + 1| + c.
x
x +1
IV – Etude de la fonction logarithme Népérien:
1– Ensemble de définition
La fonction ln est définie et continue sur ]0 ;+∞[.
2 – Limites aux bornes
lim
x → 0+
ln x = − ∞
;
lim
ln x = + ∞ .
x →+∞
3 – Fonction dérivée
La fonction ln est dérivable donc continue sur ]0 ; +∞[.
f (x) = lnx ⇒ f Ʌ ( x) =
1
> 0 ∀ x ε ]0 ;+∞[.
x
D’où ln est strictement croissante sur ]0 ;+∞[.
Cours Fonction logarithme
Page 2 sur 5
Adama Traoré Professeur Lycée Technique
4– Bijectivité – Nombre e :
La fonction ln est continue et strictement croissante sur ]0 ;+∞[. C’est donc
une bijection de ]0 ;+∞[ sur ℝ.∀yεℝ;∃ ! xε]0 ;+∞[ tel que lnx = y.
Pour y = 1 l’équation ln(x) = 1 admet une solution unique x = e ≈ 2,71.
2,718 ≤ e ≤ 2,719.
Définition :
On appelle base du logarithme Népérien l’unique nombre réel e tel que
. lne = 1.
5 – Etude des branches infinies :
a-/ Comportement asymptotique au voisinage de zéro :
lim f ( x) = −∞ || donc la droite d’équation x = 0 est Asymptote Verticale.
x → 0+
b-/ Comportement asymptotique au voisinage de + ∞ :
Soit f (x) = lnx ;
lim f ( x) = + ∞ . On cherche
lim
x→+∞
x→+∞
f ( x)
.
x
En effet pour tout réel x strictement positif on a : lnx ≤ x ; ⇒
De plus si x >1 on a : 0 ≤
0 ≤ xlim
→+∞
ln x
≤
x
x
x
⇔
0≤ xlim
→+∞
ln x
≤ 0. D’après le théorème des gendarmes :
x
ln x
≤
x
x
x
lim
x
⇔
x
ln x
≤
x
lim
x→+∞
x→+∞
ln( x)
=0 .
x
D’où la droite d’équation y = 0 est une direction parabolique.
- Conséquences :
lim
x → 0+
.
x ln x = 0 ;
x → 0+
x n ln x = 0 ;
lim
x→0
ln( x + 1)
=1
x
;
ln x
lim x − 1
= 1 .
x →1
lim x ln x = (0) × (−∞) Forme indéterminée.
x → 0+
Posons x =
Donc
.
lim
lim
x→0
1
; si x → 0
X
lim + x ln x = lim
X → +∞
x→0
alors X → +∞
∞.
1  1 
1
(ln 1 − ln X ) = lim −  ln X  = 0 .
ln   = lim
X → +∞
X  X  X → +∞ X
 X 
ln( x + 1) 0
=
Forme indéterminée.
x
0
Posons x + 1 = h
Donc
+
lim
x→0
⇔ x = h – 1 ; si x → 0 alors
h → 1.
ln( x + 1)
ln(h) − ln(1)
= lim
= ln' (1) = 1 .
h →1
x
h −1
Cours Fonction logarithme
Page 3 sur 5
Adama Traoré Professeur Lycée Technique
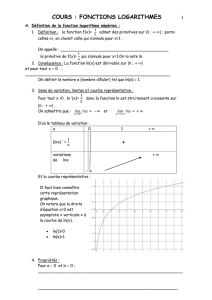
6 – Tableau de variation de ln :
x
e
1
0
1
x
+
+
+
+∞
+∞
lnx
1
–∞
0
Remarques importantes :
• Si x ε ]0 ; 1[ alors lnx < 0 ;
• Si x ε ]1 ; +∞[ alors lnx > 0 .
- Equation de la tangente (T) en x0 = 1 :
(T) : y = f ' ( x 0 ) ( x − x 0 ) + f ( x 0 ) ⇔ (T) : y = x − 1 .
7 – Tracé de la courbe de ln :
y
y = lnx
2
1
(T )
0
–1
1
2
e
3
4
x
–2
Cours Fonction logarithme
Page 4 sur 5
Adama Traoré Professeur Lycée Technique
V – Logarithme de base a (a ε ℝ *+ ; et a ≠ 1) :
1-/ Définition : On appelle logarithme de base a la fonction notée
log a
et définie par :
log a : ]0 ;+∞ [ -------→ ℝ
ln x
x ֏ log (ax ) =
.
ln a
Remarque : Si la base a = e, alors log ex =
. log (ax ) =
ln x
ln a
.
ln x
= ln x
ln e
2-/ Propriétés :
'
ln x 
1
a) logɅa(x) = 
;
 =
 ln a  ln a × x
u ' ( x)
1 u ' ( x)
b) (loga o u)Ʌ(x) =
=
×
.
u ( x) ln a ln a u ( x)
 x 
c) loga   = log ax − log ay ;
 y 
d) loga( x × y) = log ax + log ay ;
e) loga( x r ) = r × log ax ;
f) loga 
1
y
 = − log a ;
x
 
ln a
g) log aa =
= 1.
ln a
3-/ Logarithme décimal ( log à base dix)
On définit le logarithme décimal noté log par : log 10( x ) = log ( x) =
log10 = log 1010 =
ln x
.
ln 10
ln 10
3
= 1 . D’où log10 = 1 et log10 = 3 log10 = 3.
ln 10
Cours Fonction logarithme
Page 5 sur 5
Adama Traoré Professeur Lycée Technique