Calcul différentiel

Tale ST I Calcul différentiel 2008-2009
Calcul différentiel
Table des matières
I Dérivation 2
I.1 Nombre dérivé en un point . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
I.2 Fonction dérivée . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
I.3 Dérivées successives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
I.4 Opérations .............................................. 4
I.5 Équation de la tangente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
II Étude des variations d’une fonction 5
II.1 Lien entre dérivation et sens de variation d’une fonction . . . . . . . . . . . . . . . . . . . . . 5
II.2 Extremum d’une fonction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
II.3 Résolution de l’équation f(x) = λ.................................. 7
III Primitives 8
III.1Définitions............................................... 8
III.2 Calculs de primitives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
III.2.1 Primitives des fonctions usuelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
III.2.2 Opérations sur les primitives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
http://nathalie.daval.free.fr -1-

Tale ST I Calcul différentiel 2008-2009
I Dérivation
Dans cette partie, fest une fonction numérique définie sur un intervalle I,Csa courbe représentative dans
un repère. aet xsont deux réels distincts de I
I.1 Nombre dérivé en un point
Définition 1
Soit fune fonction définie en aet au voisinage de a, on dit que fest dérivable en as’il existe un réel A
est une fonction ǫtels que, au voisinage de h= 0, on a :
f(a+h) = f(a) + Ah +hǫ(h),avec lim
h→0ǫ(h) = 0.
A est appelé nombre dérivé de fen a.
Exemple 1
On considère la fonction définie sur Rpar f(x) = x2.
➔f(a+h) = (a+h)2=a2+ 2ah +h2=f(a) + (2a)h+h(h).
➔Donc, fest dérivable en ade nombre dérivé A= 2aet ǫ(h) = hde limite nulle en 0.
Définition 2
➤Le taux de variation de la fonction fentre aet xest le quotient : f(x)−f(a)
x−a.
➤Avec x=a+h, ce quotient s’écrit aussi : f(a+h)−f(a)
h.
➤fest dérivable en aet on note cette dérivée f′(a)si la limite suivante existe :
f′(a) = lim
h→0
f(a+h)−f(a)
h.
Exemple 2
Soit fdéfinie sur Rpar f(x) = x2.
➔le taux de variation de fentre aet a+hest :
f(a+h)−f(a)
h=(a+h)2−a2 h=a2+ 2ah +h2−a2 h=2ah +h2 h= 2a+h.
➔donc, f′(a) = lim
h→0(2a+h) = 2a.
➔En particulier, f′(3) = 6,f′(0) = 0 ...
Interprétation graphique :
Lorsque hse rapproche de 0, le point
Mse rapproche du point A.
Ainsi, la droite (AM) se rapproche
de la tangente Tau point A
f′(a) correspond au coefficient di-
recteur de la tangente Tau point
d’abscisse a.A
a
f(a)
M
a+h
f(a+h)T
http://nathalie.daval.free.fr -2-

Tale ST I Calcul différentiel 2008-2009
I.2 Fonction dérivée
Définition 3
Soit fune fonction dérivable en tout point xd’un intervalle I, alors la fonction qui à xassocie f′(x)est
appelé fonction dérivée de fsur I.
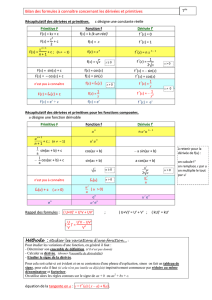
On obtient le tableau de dérivation suivant :
Fonction fFonction f′Ensemble de définition de f
k0R
ax +b a R
1
x−1 x2R∗
√x1
2√xR∗
+
xααxα−1Rsi α∈N∗ou R∗si α∈Z∗
−ou R∗ +si α∈R
ln(x)1
xR∗
+
exexR
sin(x) cos(x)R
cos(x)−sin(x)R
Exemple 3
Calcul de la dérivée des fonctions suivantes :
➔f(x) = π f ′(x) = 0 ➔f(x) = x3f′(x) = 3x2
➔f(x) = x2
3f′(x) = 2
3x−1
3➔f(x) = x2007 f′(x) = 2007x2006
I.3 Dérivées successives
Définition 4
Soit fune fonction dérivable. Lorsque cela est possible, on définit les dérivées successives de fnotées :
f′, f′′ , f ′′′ , . . . , f (n).
Exemple 4
Soit fla fonction définie sur Rpar f(x) = 2x3−x2+x+ 3.
➔f′(x) = 6x2−2x+ 1.
➔f′′ (x) = 12x−2.
➔f′′′ (x) = 12.
➔f(4) = 0.
En physique et en mécanique, on utilise la notation différenteielle : df
dx =f′et d2f dx2=f′′
Exemple 5
Dans un circuit R, L, C en série, on a :
➔i=dq
dt .
➔e=−Ldi
dt.
➔donc : e=−Ld2q
dt2.
R L C
http://nathalie.daval.free.fr -3-

Tale ST I Calcul différentiel 2008-2009
I.4 Opérations
uet vsont deux fonctions définies et dérivables sur un même intervalle I.
Opération Fonction Dérivée
Addition u+v u′+v′
Multiplication par un nombre k×uavec k∈Rk×u′
Multiplication u×v u′×v+u×v′
Puissance unn×u′×un−1
Division u
v
u′×v−u×v′
v2
Inverse 1
v−v′ v2
Fonction composée f◦g f′◦g×g′
exponentielle euu′eu
logarithme ln(u)u′
u
sinus sin(u)u′cos(u)
cosinus cos(u)−u′sin(u)
Exemple 6
Calcul de dérivées :
➔f(x) = x3+x+ 3 : On utilise la formule (u+v)′=u′+v′avec u(x) = x3et v(x) = x+ 3.
on obtient f′(x) = 3x2+ 1.
➔f(x) = 3(x2+ 4) : on utilise la formule (ku)′=ku′avec k= 3 et u(x) = x2+ 4.
on obtient f′(x) = 6x.
➔f(x) = (−2x+ 3)(5x−3) : On utilise la formule (uv)′=u′v+uv′avec u(x) = −2x+ 3 et v(x) = 5x−3.
on obtient f′(x) = −20x+ 21.
➔f(x) = (2x−7)2: on utilise la formule (u2)′= 2uu′avec u(x) = 2x−7.
on obtient f′(x) = 4(2x−7).
➔f(x) = 3x−4
x2+ 3 : On utilise la formule u v′
=u′v−uv′
v2avec u(x) = 3x−4et v(x) = x2+ 3.
on obtient f′(x) = −3x2+ 8x+ 9
(x2+ 3)2.
➔f(x) = 1
−3x+ 1 : On utilise la formule 1 v′
=−v′
v2avec v(x) = −3x+ 1.
on obtient f′(x) = 3
(−3x+ 1)2.
➔f(x) = e3x+1 : On utilise la formule (eu)′=u′euavec u(x) = 3x+ 1.
on obtient f′(x) = 3 e3x+1.
➔f(x) = ln(−2x+ 5) : On utilise la formule (ln u)′=u′
uavec u(x) = −2x+ 5.
on obtient f′(x) = −2
−2x+ 5.
➔f(x) = cos(2x+ 1) : On utilise la formule cos′(u) = −u′sin(u)avec u(x) = 2x+ 1.
on obtient f′(x) = −2 sin(2x+ 1).
http://nathalie.daval.free.fr -4-

Tale ST I Calcul différentiel 2008-2009
I.5 Équation de la tangente
Propriété 1
Soit fune fonction numérique définie sur un intervalle Iet dérivable en a∈I.
La tangente Taen aà la courbe Cfa pour équation :
Ta:y=f′(a)(x−a) + f(a).
Exemple 7
Soit f(x) = x2+ 2. Les équations des tangentes en 0et en −1sont :
➔f′(x) = 2x
➔f′(0) = 0 donc T0:y= 0 ×(x−0) + f(0) = 2.
➔f′(−1) = −2donc T−1:y=−2×(x+ 1) + f(−1) = −2x+ 1.
II Étude des variations d’une fonction
II.1 Lien entre dérivation et sens de variation d’une fonction
L’idée est qu’il y a un lien entre le signe du coefficient directeur de la tangente de la courbe Cet le sens de
variation de la fonction f.
Propriété 2
On suppose que fest dérivable sur I.
♦fest croissante sur I⇐⇒ f′(x)>0 pour tout x∈I.
♦fest décroissante sur I⇐⇒ f′(x)60 pour tout x∈I.
♦fest constante sur I⇐⇒ f′(x) = 0 pour tout x∈I.
Il est donc possible de déterminer les variations d’une fonction à partir du signe de sa dérivée.
Exemple 8
Étude d’une fonction polynôme :
Soit f(x) = 2x3−3x2−12x−1, définie et dérivable sur R. Déterminons son sens de variation :
➔Pour tout réel xon a f′(x) = 6x2−6x−12 = 6(x2−x−2).
➔On détermine le signe de x2−x−2en cherchant ses racines et on trouve −1et 2.
f′(x) = 6(x+ 1)(x−2) est positive sauf entre ses racines −1et 2.
➔On peut déterminer le signe de la dérivée et en déduire les variations de la fonction f:
x−∞ −1 2 +∞
signe de f′(x) + 0 −0 +
6 +∞
variations de fր ց ր
−∞ −21
➔fest croissante sur ]− ∞ ;−1 ] et sur [ 2 ; +∞[et décroissante sur [−1 ; 2 ].
http://nathalie.daval.free.fr -5-