2nde-fonctions-homog.. - Mathématiques au lycée Bellepierre

Chapitre 11 – Fonctions homographiques TABLE DES MATIÈRES – page -1
Chapitre 11 – Fonctions homographiques
Table des matières
I Exercices I-1
1 Fonctioninverse....................................... I-1
2 Une courbe de fonction homographique en détail . . . . . . . . . . . . . . . . . . . . . I-1
3 ................................................ I-2
II Cours II-1
1 Fonctioninverse.......................................II-1
2 Fonctions homographiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II-1
2a Définition et exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II-1
2b Ensemble de définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II-1
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr

Chapitre 11 – Fonctions homographiques I EXERCICES – page I-1
I Exercices
1 Fonction inverse
La fonction fest définie par f(x) = 1
x, on l’appelle la fonction inverse parce que 1 xest l’inverse de x.
1. Compléter le tableau ci-dessous.
x−5−4−2−1−0,5−0,2 0 0,2 0,5 1 2 4 5
1
x
2. Compléter ci-dessous la représentation graphique de la fonction f.
1
2
3
4
−1
−2
−3
−4
−5
1 2 3 4−1−2−3−4−5
2 Une courbe de fonction homographique en détail
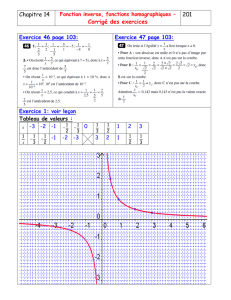
On considère la fonction définie par f(x) = −2x+ 4
x−3.
1. Compléter les tableaux de valeurs en haut de la page suivante. Arrondir au 10e.
2. Pour une certaine valeur de x, on constate que f(x) n’est pas défini (n’existe pas). Pour quelle
valeur de x?
3. Tracer soigneusement la représentation graphique de la fonction fdans le repère de la page
suivante.
4. Dresser le tableau de variation de la fonction f.
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr

Chapitre 11 – Fonctions homographiques I EXERCICES – page I-2
x−4−2 0 1 1,5 2 2,5 2,75
f(x)
x3 3,3 3,5 4 4,5 5 7 10
f(x)
1
2
3
4
−1
−2
−3
−4
−5
−6
−7
−8
−9
123456789−1−2−3−4
3
1. Déterminer l’ensemble de définition de la fonction fdéfinie par f(x) = 1
x
2. Même question dans chacun des cas suivants : (a) f(x) = −2x+ 4
x−3(b) f(x) = 4x−3 x−5
(c) f(x) = 2x
x+ 4 (d) f(x) = x−3 x(e) f(x) = −4 2x+ 3 (f) f(x) = 2x+ 7 3x−5
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr

Chapitre 11 – Fonctions homographiques II COURS – page II-1
II Cours
1 Fonction inverse
Capacités attendues
– Connaître les variations de la fonction inverse.
– Représenter graphiquement la fonction inverse.
Définition
La fonction inverse est définie par f(x) = 1
x
Ensemble de définition
On sait que 1
0n’existe pas donc la fonction in-
verse n’est pas définie lorsque x= 0.
– On dit que : la fonction inverse est définie sur
]− ∞ ; 0[ ∪]0 ; +∞[
– ou que : l’ensemble de définition de la fonc-
tion inverse est ] − ∞ ; 0[ ∪]0 ; +∞[
Tableau de variations
x−∞ 0+∞
1
x
Représentation graphique : voir exercice 1
2 Fonctions homographiques
Capacité attendue : identifier l’ensemble de définition d’une fonction homographique.
2a Définition et exemples
Définition
Soient quatre nombres a,b,c,d, tels que c6= 0 Une fonction fdéfinie par f(x) = ax +b
cx +dest
appelée une fonction homographique.
Exemple de fonction homographique : voir exercice 2 et exemples plus bas.
Remarque : la fonction inverse est une fonction homographique, en effet 1
x=0x+ 1 1x+ 0
2b Ensemble de définition
ax +b
cx +dn’est pas défini lorsque le dénominateur cx +dest égal à zéro.
Exemple 1
f(x) = −2x+ 4
x−3
La valeur de xtelle x−3 = 0 est 3.
Donc l’ensemble de définition de la fonction f
est ] − ∞ ; 3[ ∪]3 ; +∞[
Exemple 2
f(x) = −4
2x+ 3
pour trouver la valeur de xtelle 2x+ 3 = 0, on
résout l’équation.
2x+ 3 = 0
2x=−3
x=−−3
2=−1,5
Donc l’ensemble de définition de la fonction f
est ] − ∞ ;−1,5[ ∪]−1,5 ; +∞[
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr