1 Mise en équation

Université Montpellier 2
Faculté des Sciences
2012/2013
Examen Module GLME 502 (session 1)
durée 2h00
(Documents autorisés : Feuille A4 recto-verso et calculatrice)
Dans cette étude, nous souhaitons calculer les vitesses angulaires des différents segments de la jambe d’un foot-
balleur lors d’un coup franc. Ces paramètres contrôlent la trajectoire ultérieure du ballon ainsi que sa vitesse.
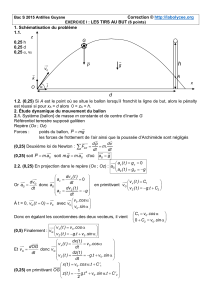
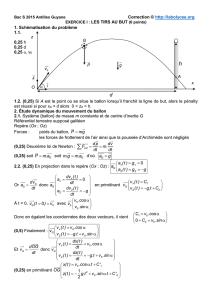
La jambe du footballeur fonctionne comme un double pendule. L’accélération transmise au ballon est maximale
lorsque les vitesses de rotation des deux articulations atteignent leurs maxima simultanément au moment de l’impact.
1 Mise en équation
On note ~uPle vecteur position du pied du joueur (= point P du pendule) et ~vPle vecteur vitesse associé dans
le repère (0, x, y, z).
1.1) Montrer que si l1et l2sont les longueurs des segments, nous avons alors
~uP= (−l1cos(θ1)−l2cos(θ2))~x + (−l1sin(θ1)−l2sin(θ2))~y
~vP= (l1˙ θ1sin(θ1) + l2˙ θ2sin(θ2))~x + (−l1˙ θ1cos(θ1)−l2˙ θ2cos(θ2))~y
1.2) On considère que les longueurs des segments l1= 0,4m et l2= 0,2√3m et que les vitesses angulaires
maximales ( ˙ θ1et ˙ θ2) sont atteintes lors de l’impact avec le ballon, c.à.d pour les angles θ1=2π
3(=π 2+π 6)
et θ2=π
6. La vitesse du ballon lors de l’impact est représenté par le vecteur ~
V=14√3
6et de norme égale
approximativement à 25 m/s (soit ≈90 km/h, vitesse moyenne pour un coup franc de Christiano Ronaldo).
Montrer que trouver les vitesses angulaires de la jambe au moment de l’impact revient à résoudre le système
linéaire AX=B avec :
A=
0,2 0,1
0,2−0,3
, X =
˙
θ1
˙
θ2
, B =
14
6
,
1

2 Résolution
2.1 Méthodes direct
2.1) Résoudre le système en utilisant la méthode de Gauss.
2.2 Méthodes itératives
2.2) Calculer les 3 premières itérées X1, X2et X3en utilisant la méthode de Jacobi en partant de X0=15
40
2.3) Pouvons nous savoir rapidement si la méthode de Gaus-Seidel est convergente dans notre cas ? Pourquoi ?
2.4) Calculer les 3 premières itérées X1, X2et X3en utilisant la méthode de Gauss-Seidel en partant de
X0=15
40
2.5) Quelle méthode converge le plus rapidement : Jacobi ou Gauss-Seidel ?
3 Cas d’une frappe horizontale au raz du sol
Ici, nous considérons que le tireur frappe le ballon de sorte que la trajectoire du ballon soit horizontale (i.e la
projection du vecteur vitesse du point Psur l’axe des yest nulle), et nous supposons également que θ1(t) = αt +2π
3
de façons à obtenir une vitesse de rotation constante de la hanche et à étudier le mouvement de la jambe à partir
de l’impact avec le ballon (avec α > 0).
3.1) Montrer que nous avons l’équation différentielle suivante :
l2˙ θ2cos(θ2) = −l1αcos(αt +2π
3).
3.2) On note hle pas de temps, ti+1 =ti+het θi
2=θ2(ti). Donner l’expression de θi+1
2, en fonction de θi
2, obte-
nue pour une méthode d’Euler explicite. Pour θ0
2=π
6,l1=l2= 0,4m,α= 20 rad/s et h= 0,02 s, calculer θ1
2et θ2 2.
3.3) Donner l’expression de θi+1
2, en fonction de θ2i, obtenue pour une méthode d’Euler d’ordre 2. Pour θ0
2=π
6,
l1=l2= 0,4m,α= 20 rad/s et h= 0,02 s, calculer θ1
2et θ2 2.
2